Следствие теоремы Лейбница (свойство остатка знакочередующегося ряда).
При доказательстве теоремы Лейбница мы показали, что 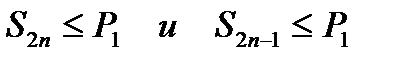 . Тогда очевидно, что и
. Тогда очевидно, что и 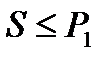 . Но так как остаток ряда
. Но так как остаток ряда 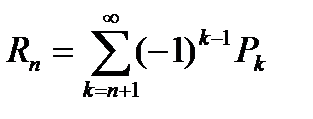 также является знакочередующимся рядом, то
также является знакочередующимся рядом, то
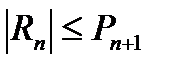 . (6.41)
. (6.41)
Отметим, что вышеуказанное свойство остатка знакочередующегося ряда дает возможность оценивать погрешности при приближенных вычислениях.
Пример 6.6. Исследуем на сходимость знакочередующийся ряд
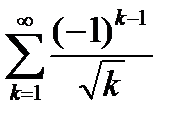 . (6.42)
. (6.42)
Решение. Заметим, что данный ряд не сходится абсолютно (см. пункт 6.3). Но так как 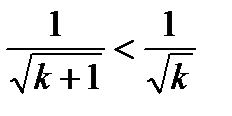 и
и 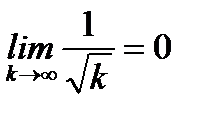 , то по признаку Лейбница ряд (6.42) сходится условно.
, то по признаку Лейбница ряд (6.42) сходится условно.
Ответ:Исходный ряд сходится условно.
Пример 6.7. Найти значение 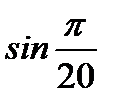 с точностью до
с точностью до 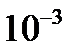 .
.
Решение. Пользуясь рядом Тейлора для 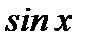 (см. пункт 6.2.3) имеем
(см. пункт 6.2.3) имеем
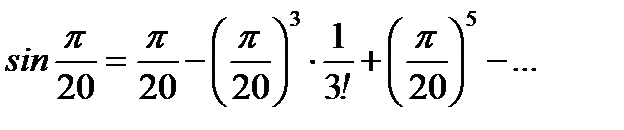 (6.43)
(6.43)
Так как 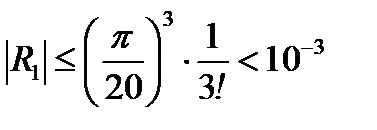 , то с точность до
, то с точность до 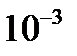 получим
получим 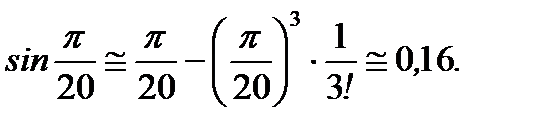
Ответ: 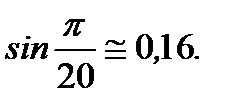
Теорема 6.18. (достаточный признак Дирихле сходимости рядов с произвольными членами). Пусть имеем ряд 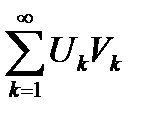 с произвольными членами. Если последовательность
с произвольными членами. Если последовательность
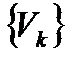 невозрастающая и
невозрастающая и 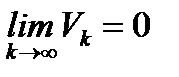 , а ряд
, а ряд 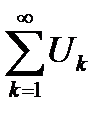 имеет ограниченную последовательность частичных сумм, то ряд
имеет ограниченную последовательность частичных сумм, то ряд 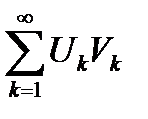 сходится.
сходится.
Пример 6.8. Исследуем на сходимость
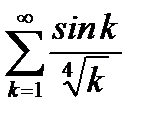 . (6.44)
. (6.44)
Решение. Возьмем 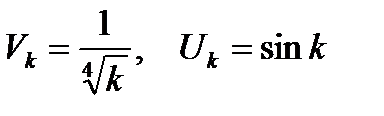 . Очевидно, что
. Очевидно, что 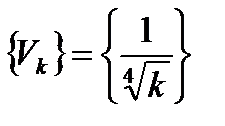 монотонно убывает и
монотонно убывает и 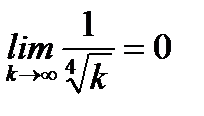 . Остается оценивать последовательность частичных сумм ряда
. Остается оценивать последовательность частичных сумм ряда 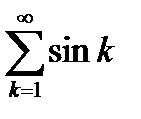 . Имеем
. Имеем 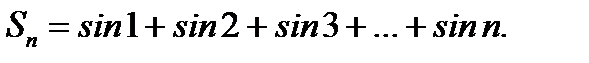 Умножив обе части этого выражения на
Умножив обе части этого выражения на 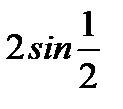 , получим
, получим 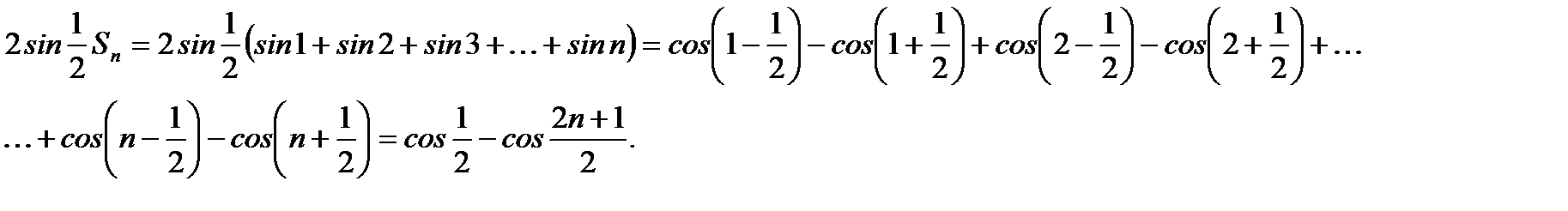 Отсюда
Отсюда
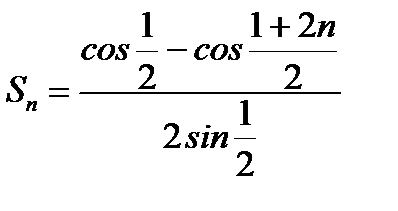 или
или 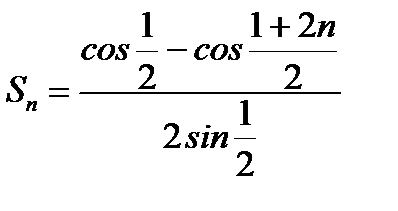 .
.
Тогда
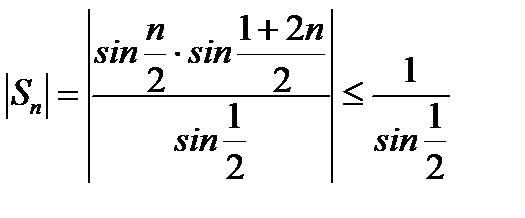 ,
,
то есть последовательность частичных сумм ряда 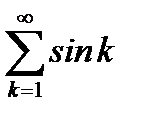 ограничена. По теореме Дирихле ряд
ограничена. По теореме Дирихле ряд 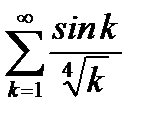 сходится.
сходится.
Ответ:Исходный ряд сходится условно.
Дата добавления: 2018-11-25; просмотров: 1263;
