Степенные ряды. Радиус сходимости.
Определение 6.14. Функциональный ряд вида
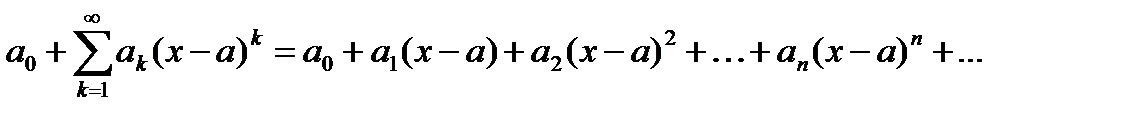 , (6.57)
, (6.57)
где 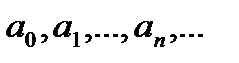 действительные числа, называется степенным рядом.
действительные числа, называется степенным рядом.
В частности, при 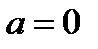 (6.57) принимает вид
(6.57) принимает вид
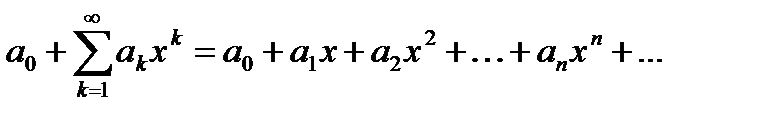 . (6.58)
. (6.58)
Теорема 6.24. (теорема Абеля).
Если степенной ряд (6.57) сходится в точке  , то он сходится (и притом абсолютно) и при всяком значении
, то он сходится (и притом абсолютно) и при всяком значении 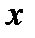 , удовлетворяющем неравенству
, удовлетворяющем неравенству
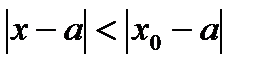 .
.
Следствие теоремы Абеля.
Для каждого степенного ряда 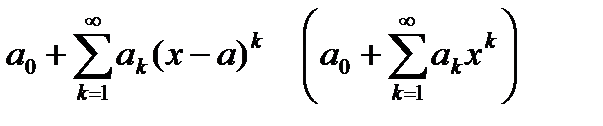 существует число
существует число  (возможно
(возможно 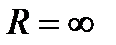 ), такое, что при
), такое, что при 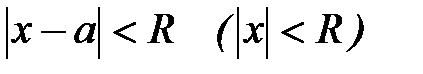 ряд абсолютно сходится, а при
ряд абсолютно сходится, а при 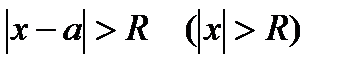 расходится. Это число
расходится. Это число 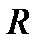 называется радиусом абсолютной сходимости степенного ряда.
называется радиусом абсолютной сходимости степенного ряда.
Получим формулы для вычисления радиуса абсолютной сходимости 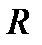 степенного ряда
степенного ряда 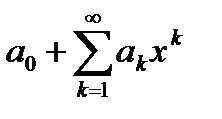 , пользуясь достаточными признаками сходимости рядов с положительными членами.
, пользуясь достаточными признаками сходимости рядов с положительными членами.
Согласно признаку Даламбера
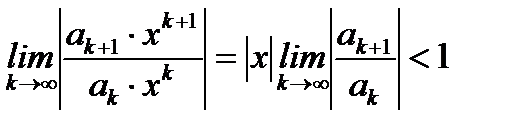 .
.
Откуда
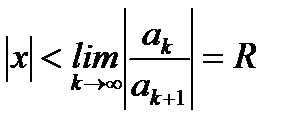 (6.59)
(6.59)
По признаку Коши
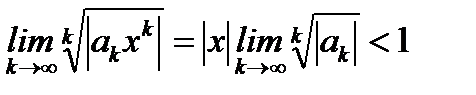
и
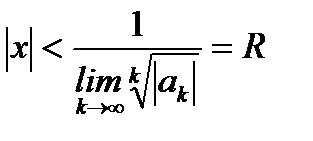 . (6.60)
. (6.60)
Если степенной ряд задан в более общем виде 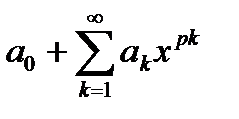 , где
, где 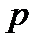 целое число >1, то радиус абсолютной сходимости этого ряда будет выражаться формулами
целое число >1, то радиус абсолютной сходимости этого ряда будет выражаться формулами
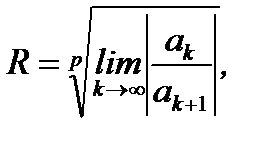
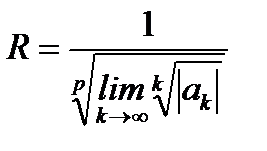 . (6.61)
. (6.61)
Замечание 6.7. Поведение степенного ряда на концах области сходимости ( 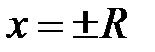 ) можно установить, исследуя сходимость соответствующих числовых рядов
) можно установить, исследуя сходимость соответствующих числовых рядов
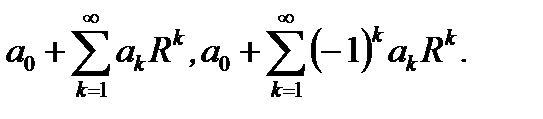
Замечание 6.8. При нахождении области сходимости степенного ряда можно пользоваться обычным методом нахождения области абсолютной сходимости функционального ряда, не вычисляя радиус сходимости 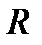 .
.
Теорема 6.25. Каково бы ни было число 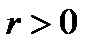 , удовлетворяющее условию
, удовлетворяющее условию 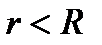 , степенной ряд
, степенной ряд 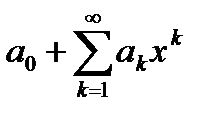 равномерно сходится на сегменте
равномерно сходится на сегменте 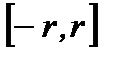 , то есть при
, то есть при 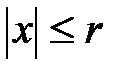 .
.
Доказательство.По теореме 6.24 исходный степенной ряд абсолютно сходится при 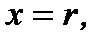 то есть абсолютно сходится числовой ряд
то есть абсолютно сходится числовой ряд 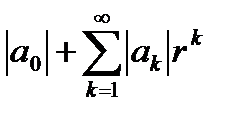 и, следовательно, он является мажорантом для степенного ряда
и, следовательно, он является мажорантом для степенного ряда 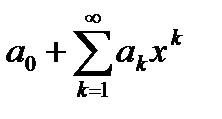 при всех
при всех 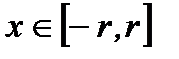 . По признаку Вейерштрасса (теорема 6.20) степенной ряд
. По признаку Вейерштрасса (теорема 6.20) степенной ряд 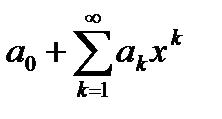 сходится равномерно на сегменте
сходится равномерно на сегменте 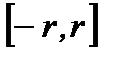 .
.
Теорема доказана.
Основываясь на теоремы 6.20, 6.21, 6.22, 6.23, 6.24 можно установить следующие свойства степенных рядов (см. теоремы 6.26, 6.27).
Теорема 6.26. Сумма степенного ряда внутри своей области сходимости является непрерывной функцией.
Теорема 6.27. Степенной ряд внутри своей области сходимости можно почленно интегрировать и почленно дифференцировать сколько угодно раз. В результате этого полученные степенные ряды имеют тот же радиус сходимости, что и исходный степенной ряд.
Пример 6.13. Найти сумму ряда
 . (6.62)
. (6.62)
Решение.Рассмотрим степенной ряд
 . (6.63)
. (6.63)
Найдем область сходимости этого ряда. По признаку Даламбера имеем
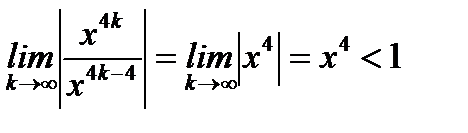 .
.
Отсюда следует, что ряд (6.63) абсолютно сходится в области 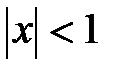 . При
. При 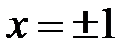 , как нетрудно заметить, ряд (6.63) расходится. Обозначим сумму ряда (6.62) через
, как нетрудно заметить, ряд (6.63) расходится. Обозначим сумму ряда (6.62) через 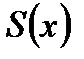
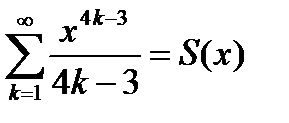 (6.64)
(6.64)
и постараемся ее найти, пользуясь формулой суммы всех членов бесконечно убывающей геометрической прогрессии, и замечая, что степенной ряд (6.63) внутри своей области сходимости можно почленно интегрировать.
Имеем с одной стороны
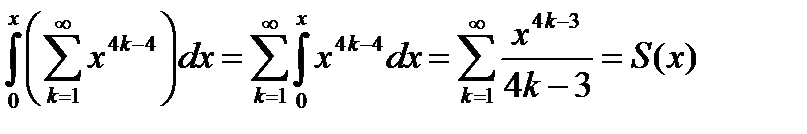 , (6.65)
, (6.65)
а с другой стороны
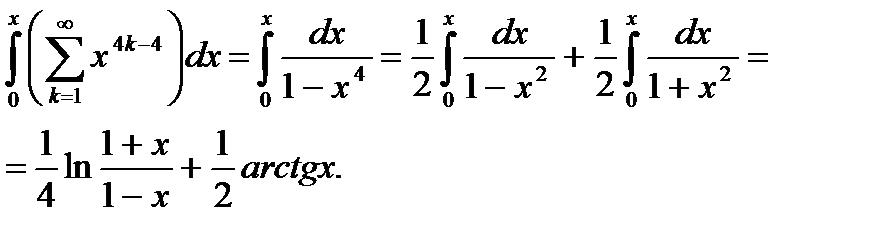 (6.66)
(6.66)
Таким образом, сравнивая (6.65) и (6.66), окончательно получим
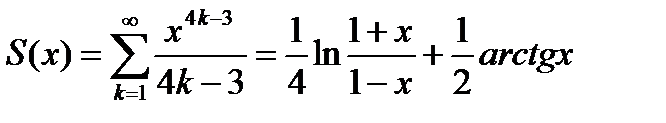 . (6.67)
. (6.67)
Ряды Тейлора.
Определение 6.15. Степенной ряд 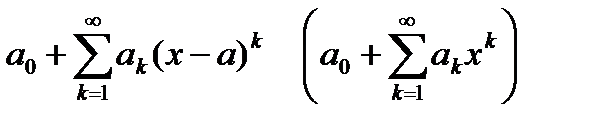 , коэффициенты которого определяются формулой
, коэффициенты которого определяются формулой 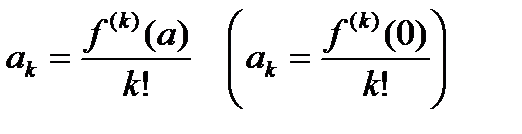 , где
, где 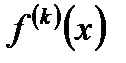 непрерывные функции в области сходимости ряда, называется рядом Тейлора функции
непрерывные функции в области сходимости ряда, называется рядом Тейлора функции 
Теорема 6.28. (необходимое и достаточное условие разложимости функции  в ряд Тейлора).
в ряд Тейлора).
Для того, чтобы функция 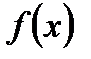 могла быть разложена в ряд Тейлора на интервале
могла быть разложена в ряд Тейлора на интервале 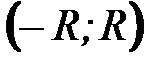 необходимо и достаточно, чтобы остаточный член в формуле Тейлора (Маклорена) для этой функции стремился к нулю при
необходимо и достаточно, чтобы остаточный член в формуле Тейлора (Маклорена) для этой функции стремился к нулю при 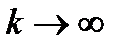 на указанном интервале
на указанном интервале 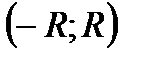 .
.
Основываясь на теорему (6.28) и вспоминая формулы Тейлора и Маклорена для функции  в окрестностях точек
в окрестностях точек  и
и 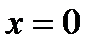 , мы получим соответствующие ряды Тейлора функции
, мы получим соответствующие ряды Тейлора функции  вокруг точек
вокруг точек 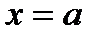 и
и  в виде
в виде
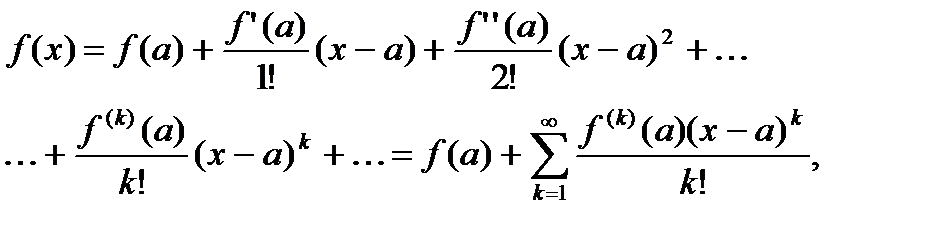 (6.68)
(6.68)
 (6.69)
(6.69)
По формуле (6.69) можно получить ряды Тейлора вокруг точки  основных элементарных функций. Ниже приведем эти ряды с указанием области их сходимости:
основных элементарных функций. Ниже приведем эти ряды с указанием области их сходимости:
 , (6.70)
, (6.70)
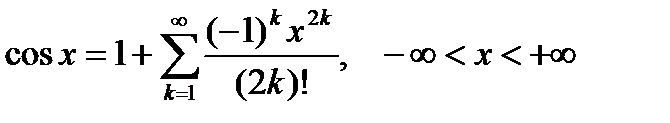 , (6.71)
, (6.71)
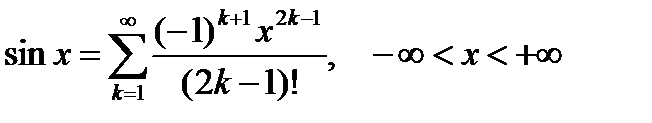 , (6.72)
, (6.72)
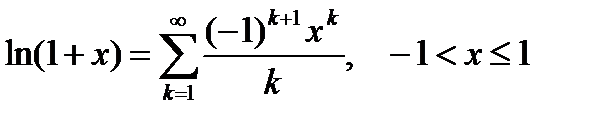 , (6.73)
, (6.73)
 (6.74)
(6.74)
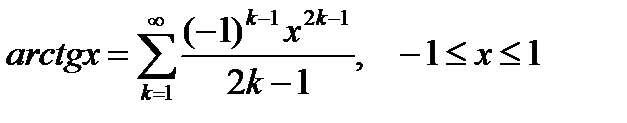 . (6.75)
. (6.75)
Замечание 6.9. С помощью разложений (6.70) – (6.75) можно провести приближенные вычисления, сохраняя в данных разложениях первые 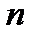 членов (
членов ( 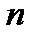 – конечное число), и отбрасывая остальные члены. Для оценки погрешности найденного приближенного значения нужно оценить сумму отброшенных членов, то есть сумму остатка ряда
– конечное число), и отбрасывая остальные члены. Для оценки погрешности найденного приближенного значения нужно оценить сумму отброшенных членов, то есть сумму остатка ряда 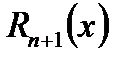 . При этом нужно иметь в виду, что если данный ряд с положительными членами, то остаток ряда
. При этом нужно иметь в виду, что если данный ряд с положительными членами, то остаток ряда 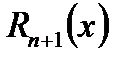 сравниваем с суммой легко суммирующегося числового ряда, члены которого больше, чем члены остатка ряда
сравниваем с суммой легко суммирующегося числового ряда, члены которого больше, чем члены остатка ряда 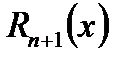 (обычно члены такого ряда составляют бесконечно убывающую геометрическую прогрессию). А если данный степенной ряд знакочередующийся, то пользуются свойством остатка такого ряда (см. следствие признака Лейбница).
(обычно члены такого ряда составляют бесконечно убывающую геометрическую прогрессию). А если данный степенной ряд знакочередующийся, то пользуются свойством остатка такого ряда (см. следствие признака Лейбница).
Замечание 6.10. Разложения элементарных функций в степенные ряды (6.70) – (6.75) могут быть применены при нахождении пределов и приближенных вычислений определенных интегралов.
Пример 6.14. Разложить в ряд Тейлора вокруг точки 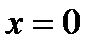 функции
функции 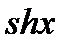 и
и 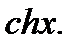
Решение:Как известно
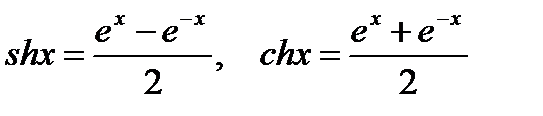 . (6.76)
. (6.76)
Подставляя в (6.76) разложения в ряд Тейлора вокруг точки 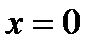 функций
функций 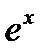 и
и  , получим
, получим
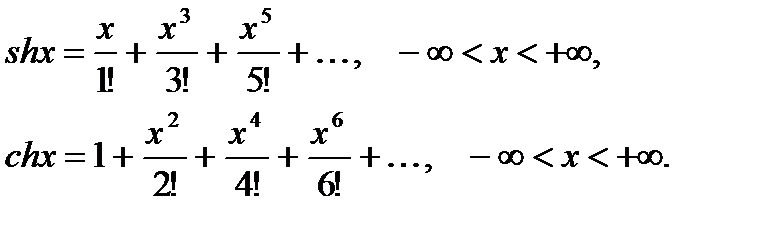 (6.77)
(6.77)
Пример 6.15. Вычислить 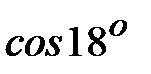 с точностью до
с точностью до 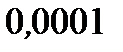 , пользуясь рядом Тейлора для c
, пользуясь рядом Тейлора для c 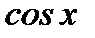 вокруг точки
вокруг точки 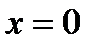 .
.
Решение:Имеем
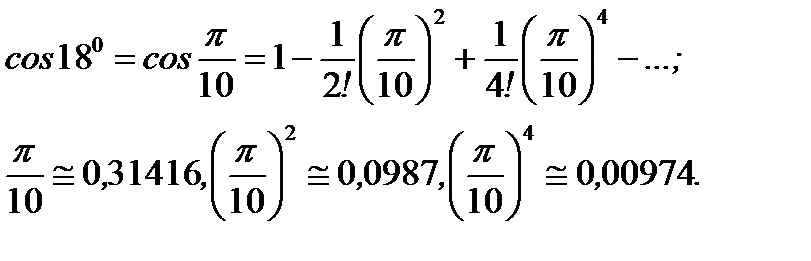
Здесь достаточно взять три члена разложения, так как 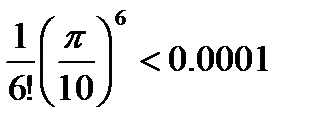 . Тогда
. Тогда

Ответ: 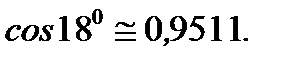
Пример 6.16. Найти 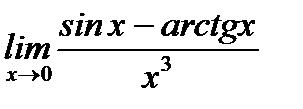 .
.
Решение: Имеем
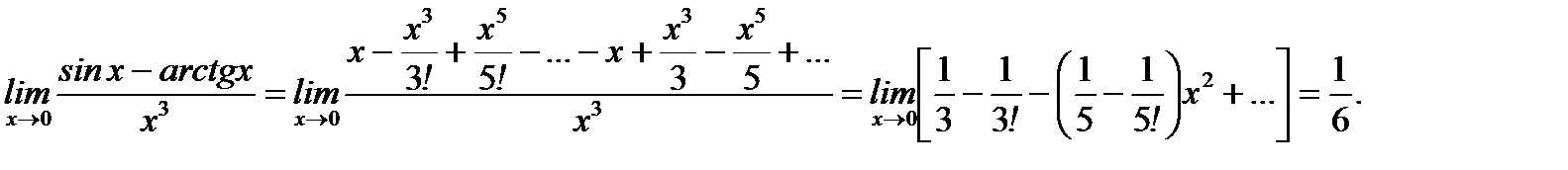
Ответ: 
Пример 6.17. Вычислить  с точностью до 0,001.
с точностью до 0,001.
Решение:Пользуясь разложением 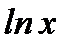 в ряд Тейлора вокруг точки
в ряд Тейлора вокруг точки 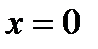 , находим
, находим
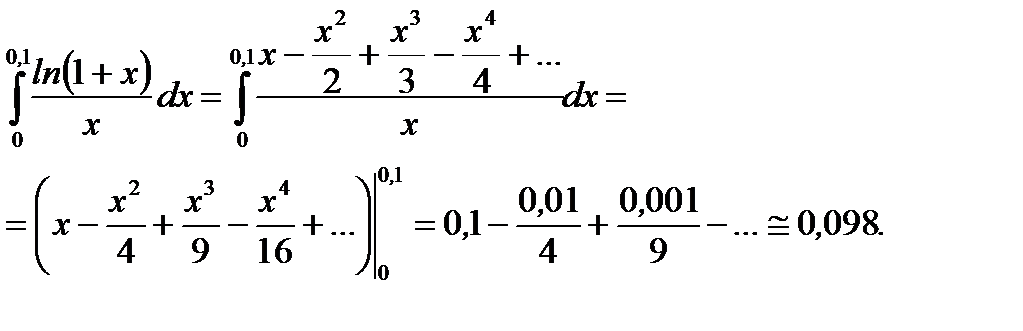
Ответ: 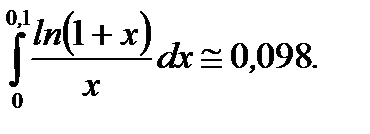
Дата добавления: 2018-11-25; просмотров: 1789;
