Примеры исследования рядов на сходимость или расходимость.

Пример 6.18. Исследовать на сходимость ряд

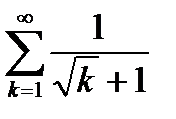. (6.78)

Решение: сначала проверим необходимое условие сходимости ряда

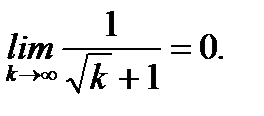
Теперь сравним ряд (6.78) с расходящимся рядом 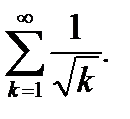По первому признаку сравнения имеем

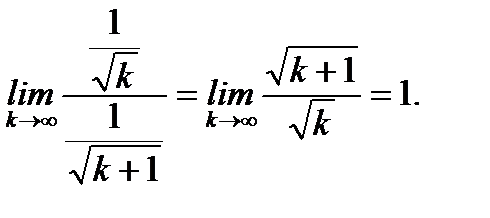
Так как единица конечное число, то из расходимости ряда 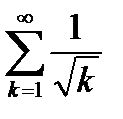следует расходимость

исходного ряда (6.78).

Ответ:Исходный ряд расходится.

Пример 6.19. Исследовать на сходимость ряд

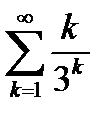.(6.79)

Решение:Проверим необходимое условие сходимости, пользуясь правилом Лопиталя

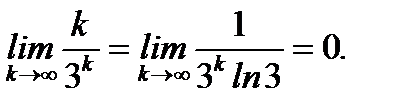
Теперь пользуемся достаточным признаком Даламбера

Так как 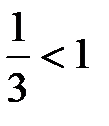, то по признаку Даламбера ряд (6.79) сходится.

Ответ:Исходный ряд сходится.

Пример 6.20. Исследовать на сходимость ряд .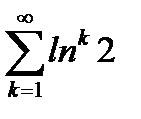

Решение:Применим достаточный признак Коши

Так как 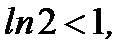то по признаку Коши исходный ряд сходится.

Ответ:Исходный ряд сходится.

Пример 6.21. Исследовать на сходимость ряд

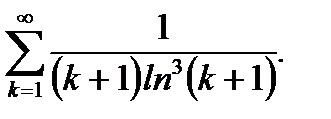(6.80)

Решение:Применим интегральный признак Коши – Маклорена

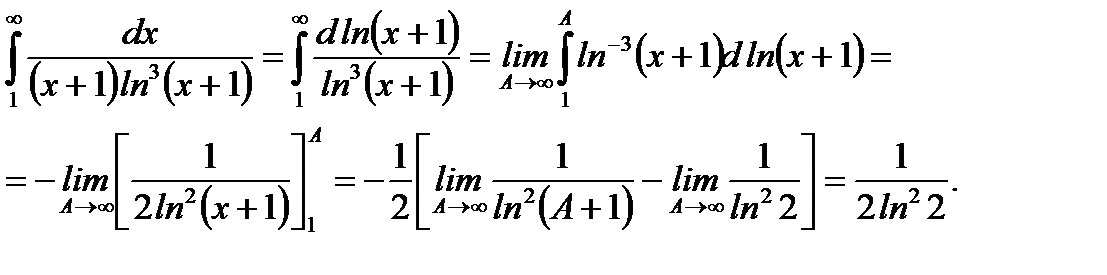
Так как 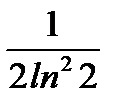конечное число, то несобственный интеграл 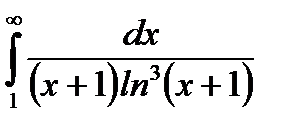сходится. По признаку Коши – Маклорена ряд (6.80) сходится.

Ответ:Исходный ряд сходится.

Пример 6.22. Исследовать на сходимость ряд с произвольными членами

. (6.81)

Решение:Применим достаточный признак Дирихле. Заметим, что последовательность 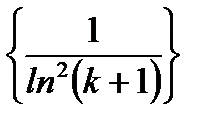монотонно убывая, стремится к нулю, а последовательность частичных сумм 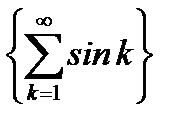ряда 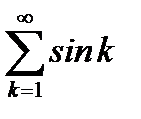ограничена

.

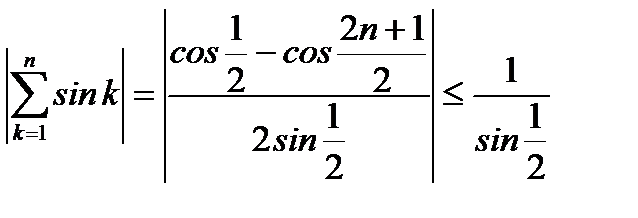По признаку Дирихле исходный ряд (6.81) сходится.

Ответ:Исходный ряд сходится.

Пример 6.23. Найти радиус абсолютной сходимости ряда

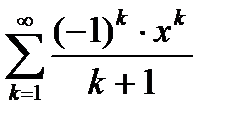(6.82)

и исследовать его сходимость на концах области сходимости.

Решение:по формуле Даламбера

.

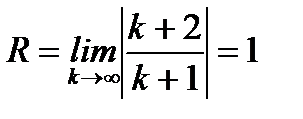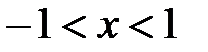Тогда ряд (6.82) сходится при или . При 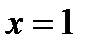имеем ряд ,

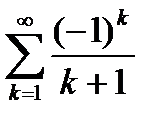который сходится по достаточному признаку Лейбница. При 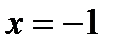имеем ряд 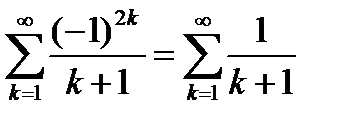, который расходится по интегральному признаку Коши – Маклорена. На самом деле, имеем

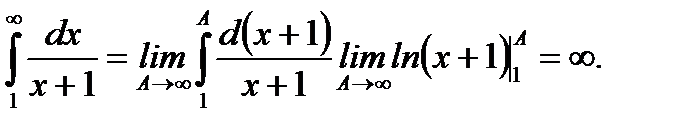
Ответ: 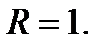Ряд сходится при

Пример 6.24. Найти радиус абсолютной сходимости ряда Тейлора для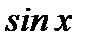

.

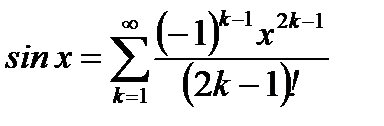Решение:По формуле (6.61) имеем

.

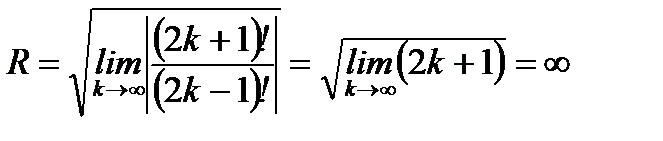Ответ: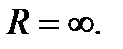

Пример 6.25. Исследовать на равномерную сходимость функциональный ряд

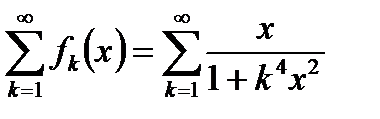при .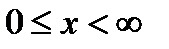

Решение:Так как 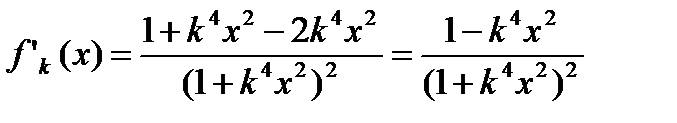, то . Легко убедиться, что в этой точке 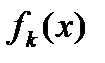имеет максимум и .

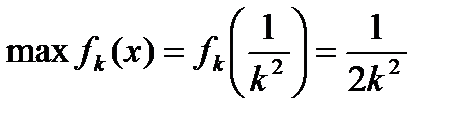Составим сходящийся ряд . Очевидно, что 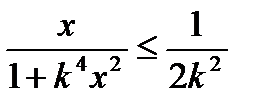и ряд 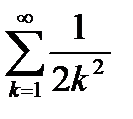является мажорантом для исходного функционального ряда. Тогда по достаточному признаку Вейерштрасса исходный ряд равномерно сходится.

Ответ:Исходный ряд равномерно сходится.

Пример 6.26. Найти сумму ряда

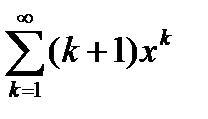. (6.83)

Решение:По формуле Даламбера для нахождения радиуса абсолютной сходимости степенного ряда имеем

.

Значит ряд (6.83) сходится при 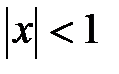. Заметим, что дифференцируя почленно степенной ряд 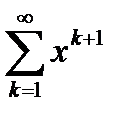внутри своей области сходимости 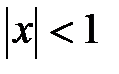, получим ряд (6.83). Но 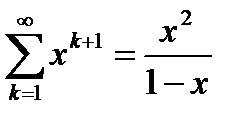по формуле суммы всех членов бесконечно убывающей геометрической

прогрессии. Следовательно, имеем

.

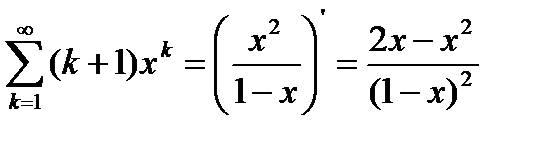Ответ: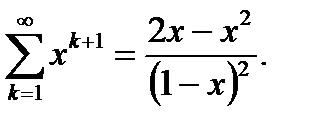

Пример 6.27. Найти область абсолютной сходимости ряда

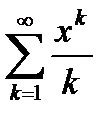. (6.84)

Решение:Найдем радиус абсолютной сходимости ряда (6.84) по формуле Даламбера

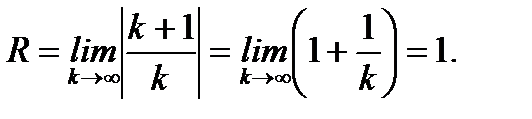
Следовательно, интервал абсолютной сходимости ряда (6.84) определяется неравенством 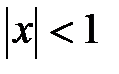. Исследуем сходимость ряда (6.84) на концах интервала. При 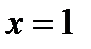из (6.84) получаем гармонический ряд 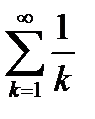, который, как известно, расходится. При 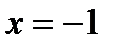из (6.84) получаем знакочередующийся ряд 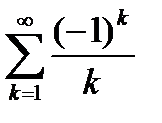, который абсолютно не сходится, но сходится условно по признаку Лейбница. Таким образом, область сходимости ряда (6.84) определяется неравенством .

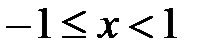Ответ:Исходный ряд абсолютно сходится при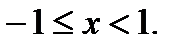

Ряды Фурье.

Определение 6.16.Функция f(x) называется периодической, если есть постоянное число 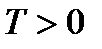такое, что 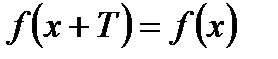для любого 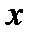из области определения функции 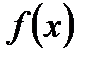. При этом 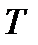называется периодом функции 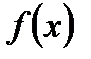. Периодические функции играют исключительную роль в биологических, химических, физических, экономических явлениях и в технике. Достаточно вспомнить любые ритмы в жизни животных, человека, растений, астрономии. Труднее назвать непериодические явления, чем периодические.

Оказалось, как заметил Фурье, многие периодические функции можно представить в виде бесконечной суммы вида (тригонометрический ряд):

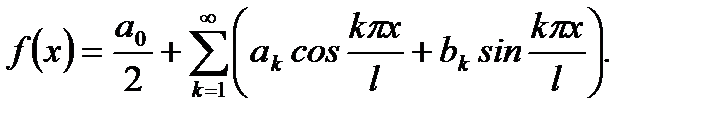(6.85)

Эта сумма называется рядом Фурье, а коэффициенты 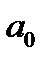, 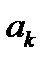и 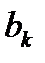вычисляются для функции с периодом 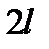по формулам

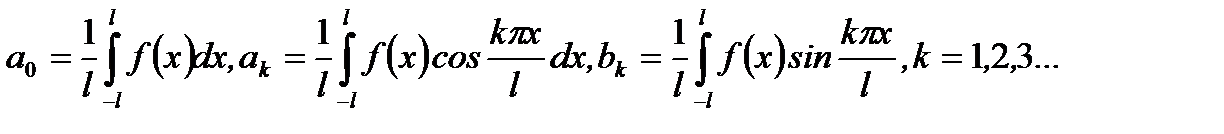(6.86)

Если функцию можно представить в виде бесконечного ряда (6.85), т.е. разложить в ряд Фурье, то такое разложение единственно.

В целях простоты изложения теоретических вопросов разложения функции в ряд Фурье предположим, что период рассматриваемой функции 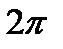. Тогда для такой функции ряд (6.85) принимает вид:

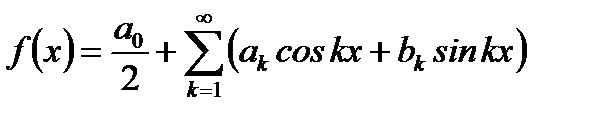, (6.87)

где

(6.88)

При вычислении коэффициентов Фурье полезно иметь ввиду, что если под интегралом в симметричных пределах от 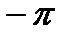до 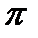стоит четная функция, то интеграл в два раза больше интеграла в пределах от 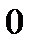до 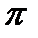, а если нечетная функция, то он равен нулю. Ниже рассмотрим эти два случая.

1. функция четная.

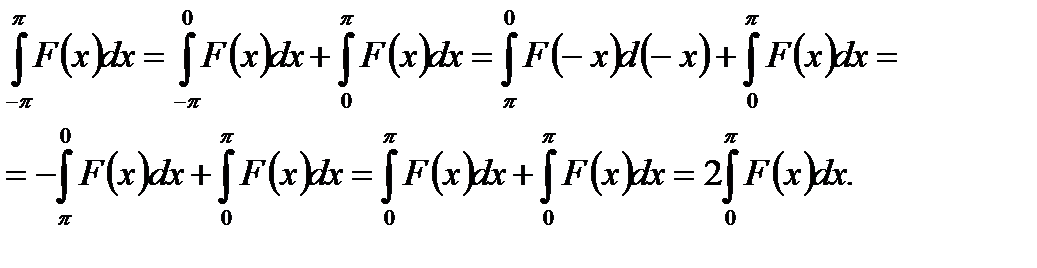(6.89)

2. 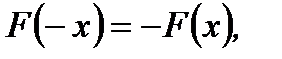функция нечетная.

(6.90)

Пример 6.28. Разложить в ряд Фурье функцию 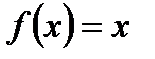на

Решение: 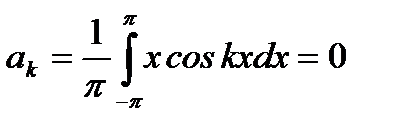, так как под интегралом стоит нечетная функция 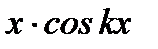, а интеграл от нечетной функции на отрезке, симметричном относительно начала координат, равен нулю (см. (6.90)). Аналогично 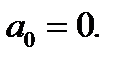При вычислении коэффициентов 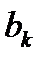нужно учитывать (6.89). Итак, имеем

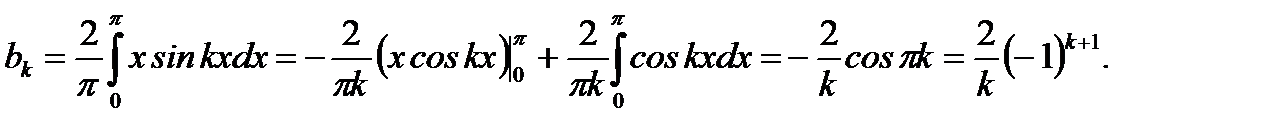(6.91)

Тогда, согласно (6.87), получим

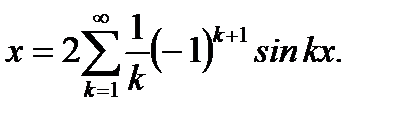
Ответ: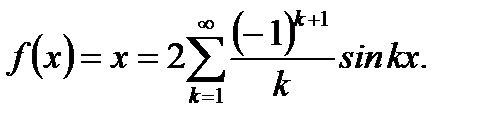

На вопрос, какую функцию можно разложить в ряд Фурье, отвечает теорема Дирихле.

Пусть функция 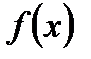удовлетворяет условиям:

1. равномерно ограничена, то есть

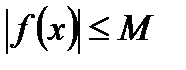при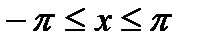

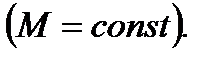
2. имеет не более, чем конечное число точек разрыва, и все они первого рода (т.е. в каждой точке разрыва 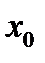функция 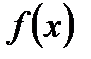имеет конечный левый предел 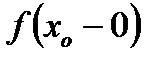и конечный правый предел .