Область сходимости функционального ряда.
Определение 6.10. Формально написанная сумма
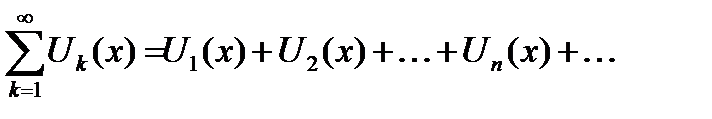 (6.45)
(6.45)
бесконечного числа членов функциональной последовательности 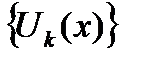 называется функциональным рядом.
называется функциональным рядом.
Предположим, что члены ряда (6.45) 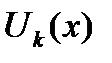 как функции от х, определены на множестве
как функции от х, определены на множестве 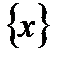 (оно является и множеством определения функционального ряда
(оно является и множеством определения функционального ряда 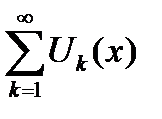 ). Фиксируем произвольную точку
). Фиксируем произвольную точку 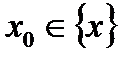 и рассмотрим ряд
и рассмотрим ряд  , являющийся числовым рядом.
, являющийся числовым рядом.
Определение 6.11. Если числовой ряд 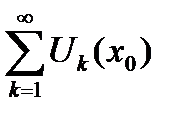 сходится, то говорят, что функциональный ряд
сходится, то говорят, что функциональный ряд 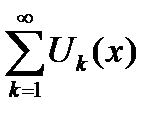 сходится в точке
сходится в точке 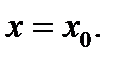
Определение 6.12. Множество всех точек 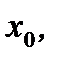 в которых сходится функциональный ряд
в которых сходится функциональный ряд 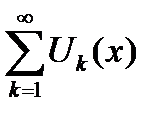 , называется областью сходимости этого функционального ряда. Область сходимости функционального ряда
, называется областью сходимости этого функционального ряда. Область сходимости функционального ряда 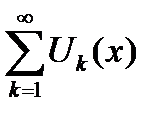 может либо совпадать с областью определения данного ряда, либо составлять часть области определения данного ряда, либо вообще являться пустым множеством.
может либо совпадать с областью определения данного ряда, либо составлять часть области определения данного ряда, либо вообще являться пустым множеством.
Если функциональный ряд 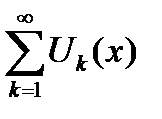 сходится на некотором множестве
сходится на некотором множестве 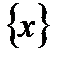 , то это означает, что
, то это означает, что 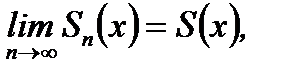 где предельная функция
где предельная функция 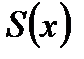 последовательности частичных сумм
последовательности частичных сумм  функционального ряда также определена на множестве
функционального ряда также определена на множестве 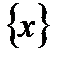 и называется суммой этого ряда.
и называется суммой этого ряда.
Пример 6.9. Найти область абсолютной сходимости функционального ряда
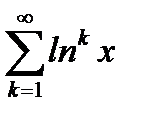 . (6.46)
. (6.46)
Решение. Составим ряд из модулей
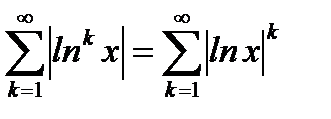 , (6.47)
, (6.47)
являющимся для произвольного 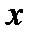 из области определения общего члена ряда (6.46) рядом с положительными членами. Воспользуемся признаком Даламбера и потребуем, чтобы ряд (6.47) сходился. Имеем
из области определения общего члена ряда (6.46) рядом с положительными членами. Воспользуемся признаком Даламбера и потребуем, чтобы ряд (6.47) сходился. Имеем
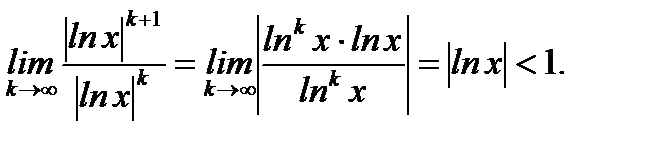
Отсюда  . Крайние точки
. Крайние точки 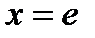 и
и 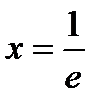 нужно проверить по отдельности, подставляя эти значения в функциональный ряд (6.46). Итак, при
нужно проверить по отдельности, подставляя эти значения в функциональный ряд (6.46). Итак, при 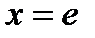 и
и 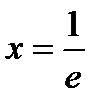 из (6.46) получаем следующие числовые ряды
из (6.46) получаем следующие числовые ряды 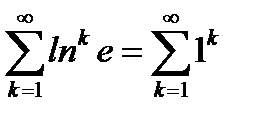 и
и 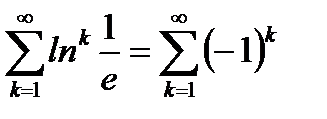 , которые, как известно (см. пункт 6.3), расходятся. Окончательно получаем, что
, которые, как известно (см. пункт 6.3), расходятся. Окончательно получаем, что 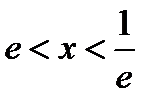 является областью сходимости функционального ряда (6.46).
является областью сходимости функционального ряда (6.46).
Ответ:Область сходимости исходного ряда определяется неравенством 
Пример 6.10. Найти область абсолютной сходимости функционального ряда
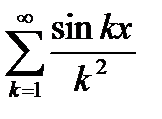 ,
,
общий член которого определен для всех  .
.
Решение. Рассмотрим ряд из модулей 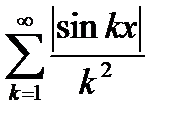 . Так как
. Так как 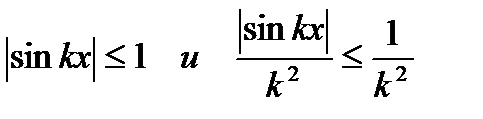 , а ряд
, а ряд 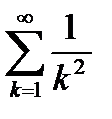 сходится, то по первому признаку сравнения, исходный ряд (6.47) абсолютно сходится для всех
сходится, то по первому признаку сравнения, исходный ряд (6.47) абсолютно сходится для всех 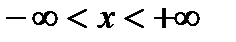 .
.
Ответ:Исходный ряд абсолютно сходится для всех 
Определение 6.13. Функциональный ряд 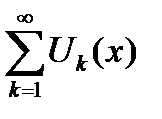 называется равномерно сходящимся на
называется равномерно сходящимся на
множестве 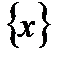 к своей сумме
к своей сумме 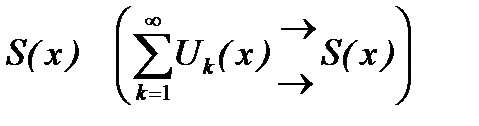 , если последовательность его частичных сумм
, если последовательность его частичных сумм 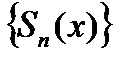 сходится равномерно на множестве
сходится равномерно на множестве 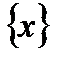 к предельной функции
к предельной функции 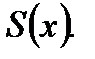
Заметим, что в символической форме определение 6.13 имеет вид
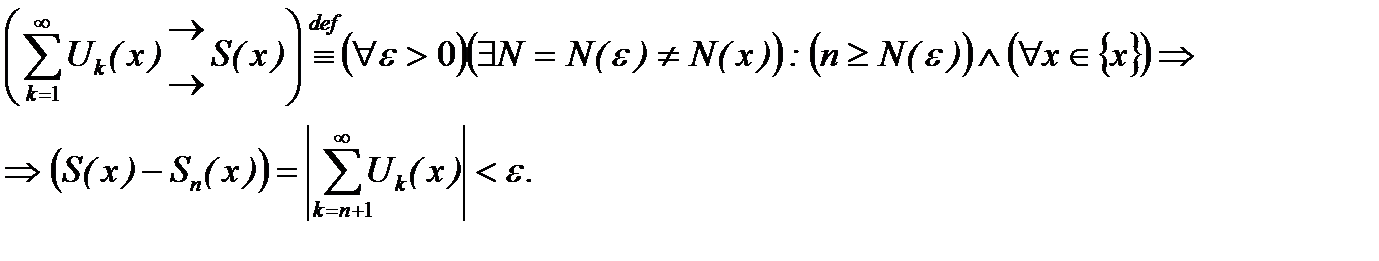 (6.48)
(6.48)
Теорема 6.19.(теорема Коши о необходимом и достаточном условии равномерной сходимости функционального ряда).
Для того, чтобы функциональный ряд 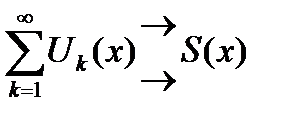 на множестве
на множестве  необходимо и достаточно, чтобы
необходимо и достаточно, чтобы
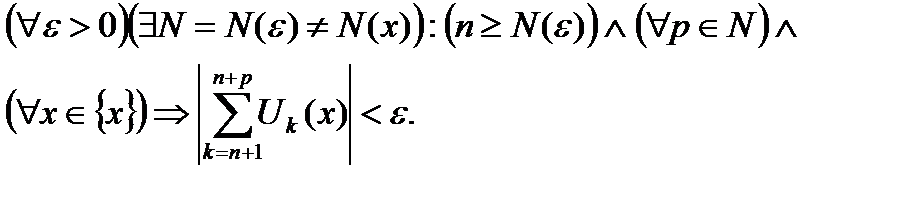
Теорема 6.20. (достаточный признак Вейерштрасса равномерной сходимости функционального ряда).
Если общий член функционального ряда 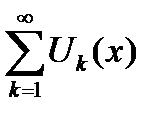 определен на множестве
определен на множестве 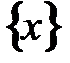 и если существует сходящийся числовой ряд
и если существует сходящийся числовой ряд 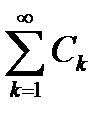 с положительными членами такой, что для всех
с положительными членами такой, что для всех 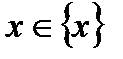 и для любого номера
и для любого номера 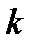 справедливо неравенство
справедливо неравенство 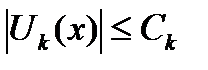 , то функциональный ряд
, то функциональный ряд  сходится равномерно на множестве
сходится равномерно на множестве 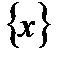 .
.
Доказательство. По условию теоремы ряд 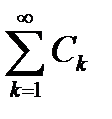 сходится. Согласно критерию Коши это означает, что
сходится. Согласно критерию Коши это означает, что
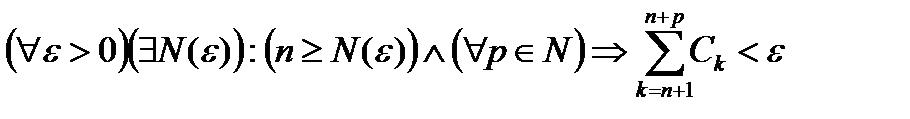 .
.
Составим 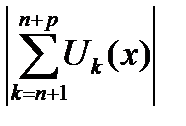 и используем условие теоремы
и используем условие теоремы  . Имеем
. Имеем
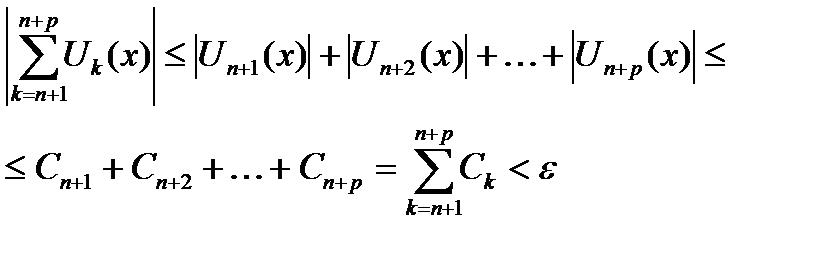 (6.49)
(6.49)
для всех 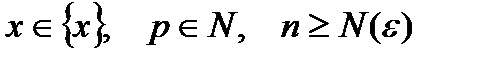 . Тогда, согласно критерию Коши, функциональный ряд
. Тогда, согласно критерию Коши, функциональный ряд 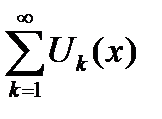 сходится равномерно на множестве
сходится равномерно на множестве 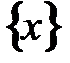 .
.
Теорема доказана.
Замечание 6.4.Сходящийся числовой ряд 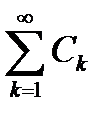 называется мажорантом для функционального ряда
называется мажорантом для функционального ряда 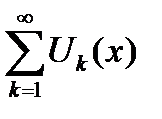 .
.
Пример 6.11. Исследовать на равномерную сходимость ряд
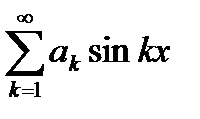 . (6.50)
. (6.50)
Решение. Так как  для
для  , то
, то 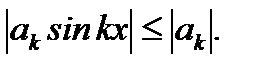 Если
Если 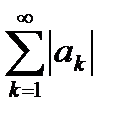 сходится, то он является мажорантом для функционального ряда (6.50) и, следовательно, по признаку Вейерштрасса, функциональный ряд (6.50) сходится равномерно.
сходится, то он является мажорантом для функционального ряда (6.50) и, следовательно, по признаку Вейерштрасса, функциональный ряд (6.50) сходится равномерно.
Ответ:Исходный ряд сходится равномерно.
Ниже некоторые важные свойства равномерно сходящихся функциональных рядов сформулируем в виде теорем.
Теорема 6.21. Если все члены функционального ряда 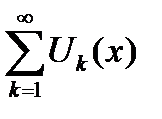 непрерывны на сегменте
непрерывны на сегменте
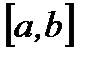 и если ряд
и если ряд 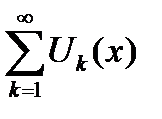 сходится к своей сумме
сходится к своей сумме 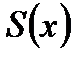 равномерно на сегменте
равномерно на сегменте 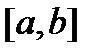 , то и сумма этого ряда
, то и сумма этого ряда 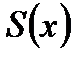 непрерывна на сегменте
непрерывна на сегменте 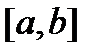 и имеет место соотношение
и имеет место соотношение

Замечание 6.5. Из теоремы (6.20) следует, что в равномерно сходящемся функциональном ряде можно местами поменять знаки суммы и предела.
Теорема 6.22. Если все члены функционального ряда 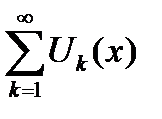 непрерывны на сегменте
непрерывны на сегменте 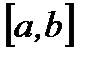 и функциональный ряд
и функциональный ряд 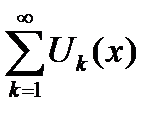 сходится к своей сумме
сходится к своей сумме 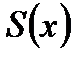 равномерно на сегменте
равномерно на сегменте 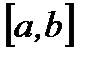 , то указанный ряд
, то указанный ряд 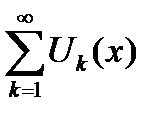 можно интегрировать на сегменте
можно интегрировать на сегменте 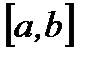 почленно, то есть
почленно, то есть
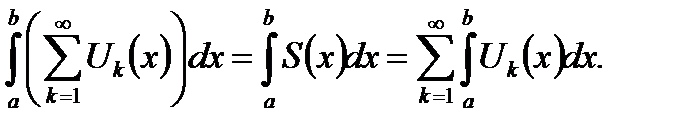 (6.51)
(6.51)
Доказательство. Так как с учетом условий теоремы имеем
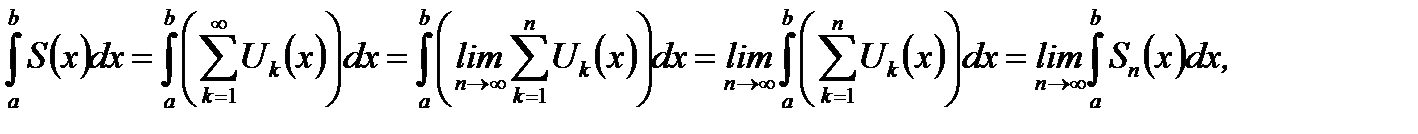
то фактически требуется доказать
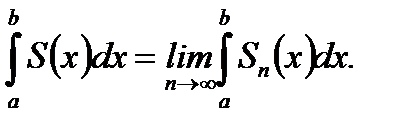 (6.52)
(6.52)
Оценим величину по модулю 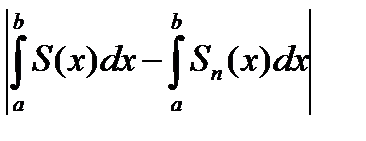 , имея в виду непрерывность функций
, имея в виду непрерывность функций 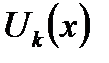 и
и 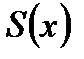 (см. теорему 6.21), и пользуясь свойствами определенного интеграла (см. часть 1). Итак
(см. теорему 6.21), и пользуясь свойствами определенного интеграла (см. часть 1). Итак
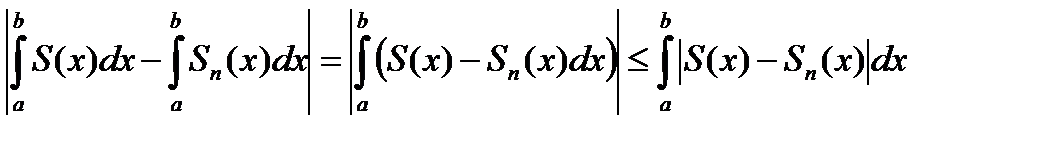 .(6.53)
.(6.53)
По определению равномерной сходимости функционального ряда 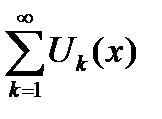 к своей сумме
к своей сумме 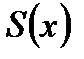 имеем
имеем
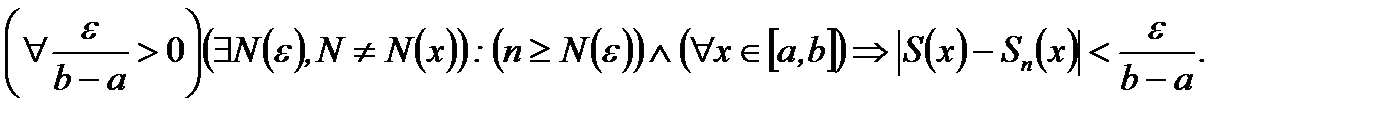 (6.54)
(6.54)
Тогда согласно (6.54) из (6.53) получим, что для  и для
и для 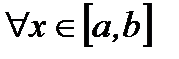 удовлетворяется неравенство
удовлетворяется неравенство
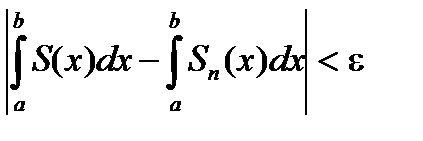 .
.
А последнее означает, что
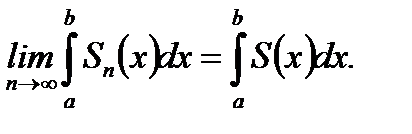
Теорема доказана.
Замечание 6.6. Из теоремы (6.22) следует, что при интегрировании равномерно сходящегося функционального ряда 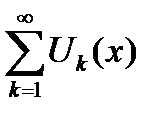 можно поменять местами знаки суммы и
можно поменять местами знаки суммы и
интеграла.
Теорема 6.23.Если функции 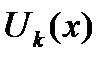 имеют производную на сегменте
имеют производную на сегменте 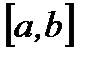 (на концах а и b существуют односторонние производные) и если ряд из производных
(на концах а и b существуют односторонние производные) и если ряд из производных 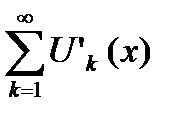 сходится равномерно на сегменте
сходится равномерно на сегменте 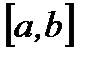 , а сам функциональный ряд
, а сам функциональный ряд 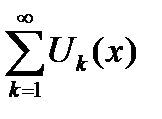 сходится хотя бы в одной точке
сходится хотя бы в одной точке 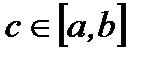 , то функциональный ряд
, то функциональный ряд 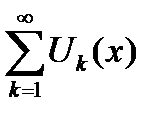 сходится равномерно на сегменте
сходится равномерно на сегменте 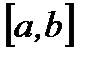 к некоторой сумме
к некоторой сумме 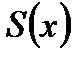 и этот ряд можно дифференцировать почленно на сегменте
и этот ряд можно дифференцировать почленно на сегменте 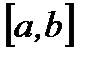 , то есть
, то есть
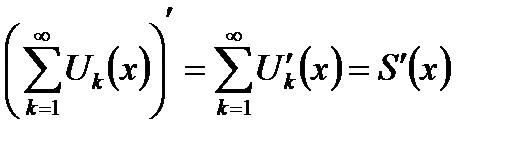 . (6.55)
. (6.55)
Пример 6.12. Пользуясь равномерной сходимостью функционального ряда, вычислить 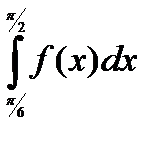 , если
, если
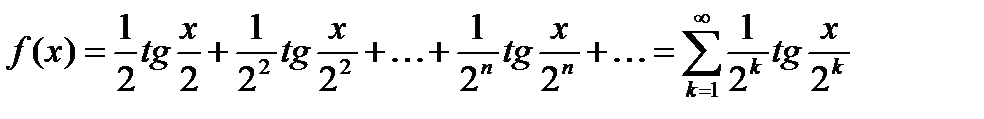 . (6.56)
. (6.56)
Решение.Так как 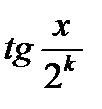 для
для 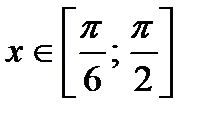 удовлетворяет условию
удовлетворяет условию 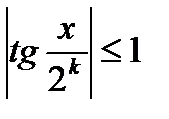 , то
, то  . Тогда сходящийся числовой ряд
. Тогда сходящийся числовой ряд 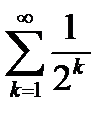 является мажорантом для функционального ряда (6.56) и последний сходится к
является мажорантом для функционального ряда (6.56) и последний сходится к 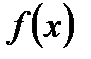 равномерно. По теореме (6.22) ряд (6.56) можно интегрировать почленно, то есть
равномерно. По теореме (6.22) ряд (6.56) можно интегрировать почленно, то есть
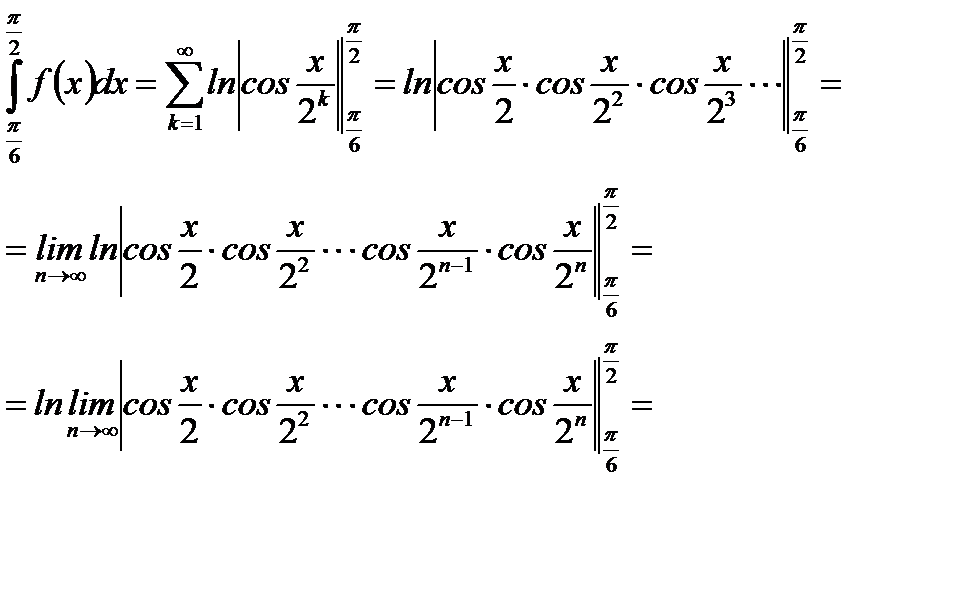
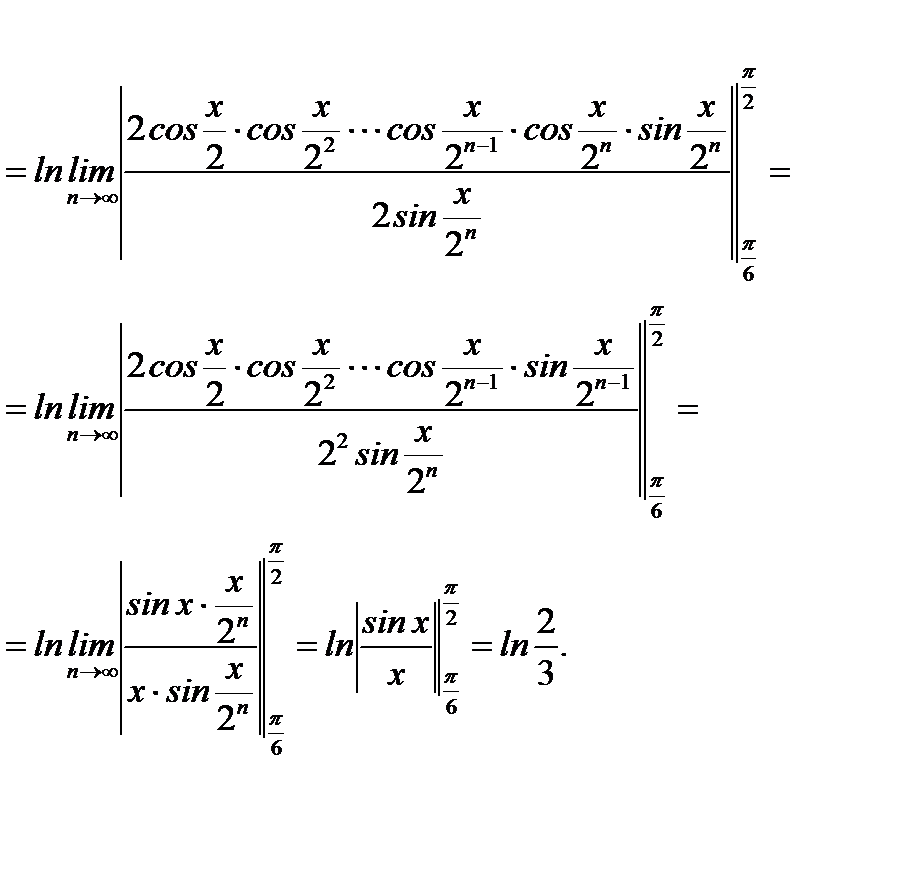
Ответ: 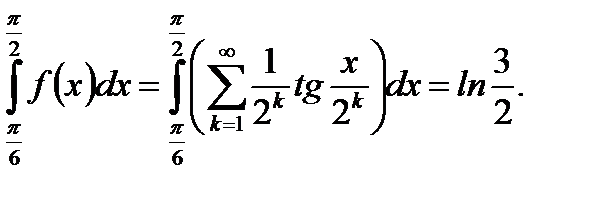
Дата добавления: 2018-11-25; просмотров: 1230;
