Знакопеременные ряды. Абсолютная и условная сходимость
Определение.Числовой ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные члены.
Теорема.Пусть 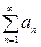 – знакопеременный ряд. Если ряд
– знакопеременный ряд. Если ряд 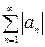 , составленный из абсолютных величин его членов, сходится, то данный ряд
, составленный из абсолютных величин его членов, сходится, то данный ряд 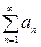 также сходится.
также сходится.
В этом случае знакопеременный ряд называется абсолютно сходящимся.
Если же знакопеременный ряд 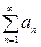 сходится, а ряд
сходится, а ряд 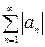 расходится, то ряд
расходится, то ряд 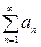 называется условно сходящимся. Сумму условно сходящегося ряда путём перестановки его членов можно сделать равной любому заданному числу.
называется условно сходящимся. Сумму условно сходящегося ряда путём перестановки его членов можно сделать равной любому заданному числу.
Для ответа на вопрос об абсолютной сходимости ряда 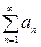 к ряду
к ряду 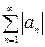 можно применять все признаки, используемые для рядов с положительными членами.
можно применять все признаки, используемые для рядов с положительными членами.
Определение.Знакочередующимсяназывается ряд, в котором любые два соседних члена имеют разные знаки, т.е. ряд:
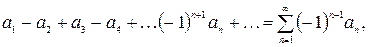 (2)
(2)
или
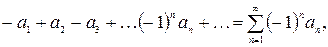 (3)
(3)
где все 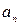 – положительные действительные числа.
– положительные действительные числа.
Признак Лейбница
Знакочередующийся ряд (2) или (3) сходится, если выполняются условия:
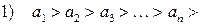 (4)
(4)
(абсолютные величины членов ряда монотонно убывают);
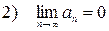 (общий член ряда стремится к нулю при
(общий член ряда стремится к нулю при 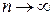 ).
).
Пример 6.Исследовать на сходимость ряд 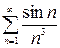 .
.
Решение. 1. Проверим, сходится ли данный знакопеременный ряд абсолютно. Для этогоисследуем на сходимость ряд, составленный из абсолютных величин членов данного ряда:
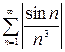 .
.
Так как
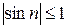 ,
,
то
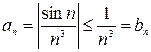 .
.
Поскольку ряд  , являющийся рядом Дирихле с
, являющийся рядом Дирихле с 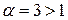 , сходится, то на основании первого признака сравнения, так как сходится больший ряд, то сходится и меньший ряд
, сходится, то на основании первого признака сравнения, так как сходится больший ряд, то сходится и меньший ряд 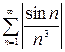 . А значит, исходный ряд сходится абсолютно.
. А значит, исходный ряд сходится абсолютно.
Пример 7.Исследовать на сходимость ряд 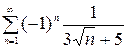 .
.
Решение. 1. Проверим, сходится ли данный ряд абсолютно. Для этогоисследуем на сходимость ряд, составленный из абсолютных величин членов данного ряда:
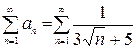 .
.
Сравним данный ряд с рядом Дирихле 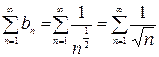 , который расходится, так как
, который расходится, так как 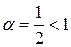 .
.
Так как
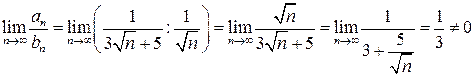 ,
,
то по второму признаку сравнения ряд 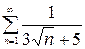 также расходится.
также расходится.
Следовательно, исходный ряд не является абсолютно сходящимся.
2. Используя признак Лейбница, выясним, является ли данный знакочередующийся ряд условно сходящимся. Для этого проверим условия (4):
1) 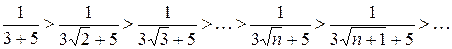
Очевидно, что данное неравенство верно для любого 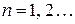
2) 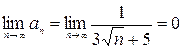 .
.
Таким образом, для данного знакочередующегося ряда выполняются условия признака Лейбница, откуда следует, что исходный ряд сходится условно.
3.5. Функциональные ряды: основные определения
Определение. Ряд, членами которого являются функции, называется функциональным, т.е. это ряд вида
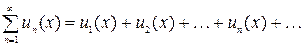 (5)
(5)
 Придавая аргументу
Придавая аргументу 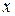 определенное значение, мы получим числовой ряд.
определенное значение, мы получим числовой ряд.
Определение.Функциональный ряд 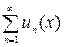 называется сходящимся в точке
называется сходящимся в точке 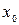 , если сходится соответствующий ему числовой ряд
, если сходится соответствующий ему числовой ряд 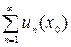 .
.
Определение. Множество всех тех значений 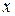 , при которых функции
, при которых функции 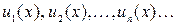 определены и функциональный ряд (5) сходится, называется областью сходимости функционального ряда.
определены и функциональный ряд (5) сходится, называется областью сходимости функционального ряда.
Определение. Функциональный ряд 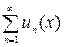 называется абсолютно сходящимся в области
называется абсолютно сходящимся в области 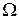 , если в этой области сходится ряд, составленный из модулей его членов, т.е. сходится ряд
, если в этой области сходится ряд, составленный из модулей его членов, т.е. сходится ряд 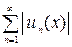 .
.
Определение.Функциональный ряд 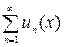 называется условно сходящимся в области
называется условно сходящимся в области  , если в этой области ряд, составленный из модулей его членов, расходится, а сам ряд сходится.
, если в этой области ряд, составленный из модулей его членов, расходится, а сам ряд сходится.
Замечание. Исследуя функциональный ряд на абсолютную сходимость можно применять признаки Даламбера или Коши. Именно, если
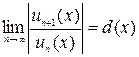
или
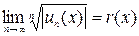 ,
,
то для определения области абсолютной сходимости функционального ряда (5) следует решить функциональное неравенство 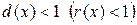 , а для определения области расходимости – функциональное неравенство
, а для определения области расходимости – функциональное неравенство 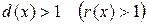 . При этом для изучения поведения ряда в граничных точках получаемой области, т.е. в точках, описываемых уравнением
. При этом для изучения поведения ряда в граничных точках получаемой области, т.е. в точках, описываемых уравнением 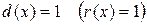 , требуется исследовать соответствующие числовые ряды, получаемые подстановкой граничных точек в функциональный ряд (5).
, требуется исследовать соответствующие числовые ряды, получаемые подстановкой граничных точек в функциональный ряд (5).
Пример 8.Найти область сходимости функционального ряда
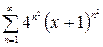 .
.
Решение.Исследуем ряд на абсолютную сходимость. Для этого рассмотрим ряд, составленный из абсолютных величин членов данного ряда
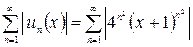 .
.
По признаку Коши
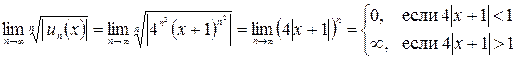 .
.
Таким образом, интервал абсолютной сходимости ряда:
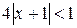 ;
;
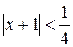 ;
;
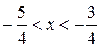 .
.
Исследуем сходимость ряда на концах интервала.
При 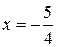 получим ряд
получим ряд
 ,
,
который расходится, так как общий член ряда не стремится к нулю, т.е. не выполняется необходимое условие сходимости ряда.
Аналогично, при 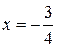 , получим расходящийся ряд
, получим расходящийся ряд
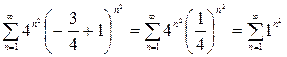 .
.
Следовательно, согласно последнему замечанию
ряд 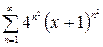 при
при 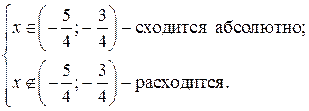
Пример 9.Найти область сходимости функционального ряда
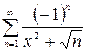 .
.
Решение. 1) Исследуем ряд на абсолютную сходимость. Зафиксируем 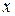 и рассмотрим ряд, составленный из абсолютных величин членов данного ряда
и рассмотрим ряд, составленный из абсолютных величин членов данного ряда
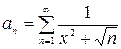 .
.
Сравним ряд из абсолютных величин с рядом Дирихле 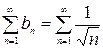 , который расходится, т.к.
, который расходится, т.к. 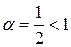 . Применим второй признак сравнения. Для этого вычислим:
. Применим второй признак сравнения. Для этого вычислим:
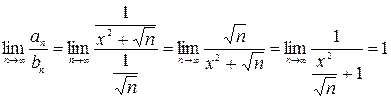 .
.
Так как получили независящий от 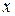 и отличный от нуля предел, то при любом
и отличный от нуля предел, то при любом 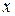 расходится и ряд
расходится и ряд 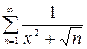 .
.
Следовательно, ряд 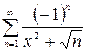 при любом
при любом 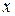 не является абсолютно сходящимся рядом.
не является абсолютно сходящимся рядом.
2) Исследуемый ряд при всех 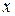 является знакочередующимся рядом. Используя признак Лейбница, выясним, является ли данный ряд условно сходящимся. Для этого проверим условия (4):
является знакочередующимся рядом. Используя признак Лейбница, выясним, является ли данный ряд условно сходящимся. Для этого проверим условия (4):
а) 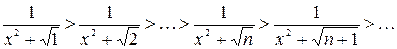
Очевидно, что данное неравенство верно для любого 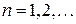 и
и 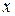 .
.
б) При всех 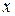 выполняется
выполняется
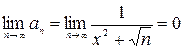 .
.
Таким образом, для данного знакочередующегося ряда при любом 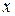 выполняются условия признака Лейбница. Следовательно, ряд
выполняются условия признака Лейбница. Следовательно, ряд 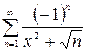 сходится условно при всех
сходится условно при всех 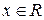 .
.
Степенные ряды
Определение.Степенным рядомназывается функциональный ряд вида
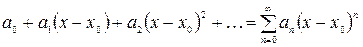 , (6)
, (6)
где 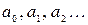 – постоянные числа, называемые коэффициентами ряда.
– постоянные числа, называемые коэффициентами ряда.
Если 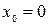 , то степенной ряд примет вид:
, то степенной ряд примет вид:
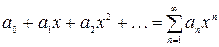 (7)
(7)
Теорема (Абеля).Если степенной ряд (6) сходится в точке 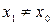 , то он абсолютно сходится в каждой точке
, то он абсолютно сходится в каждой точке 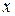 , для которой
, для которой 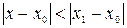 .
.
Следствие.Если степенной ряд (6) расходится при некотором значении 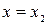 , то он расходится и при всех значениях
, то он расходится и при всех значениях 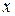 , для которых
, для которых 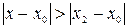 .
.
Из теоремы Абеля и её следствия следует, что для степенного ряда (6) возможны три случая:
1) ряд сходится только в точке 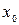 ;
;
2) ряд сходится при всех 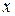 ;
;
3) существует число 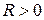 такое, что при всех
такое, что при всех 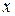 из интервала
из интервала 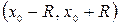 ряд сходится абсолютно, а при всех
ряд сходится абсолютно, а при всех 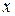 , для которых
, для которых 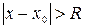 , ряд расходится.
, ряд расходится.
Определение. Радиусом сходимости ряда (6) называется число 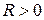 , такое, что при
, такое, что при 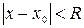 ряд сходится, а при
ряд сходится, а при 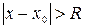 расходится. Интервал
расходится. Интервал 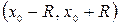 в этом случае называется интервалом сходимостиряда (6).
в этом случае называется интервалом сходимостиряда (6).
Замечание 1. Если числовой ряд (6) сходится на всей числовой оси, то полагают 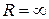 ; если он сходится только при
; если он сходится только при 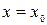 , то
, то 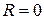 .
.
Замечание 2. На концах интервала вопрос о сходимости или расходимости данного ряда решается путём исследования соответствующих числовых рядов, получающихся при подставлении граничных значений в исследуемый ряд.
Для отыскания интервала и радиуса сходимости степенного ряда можно пользоваться одним из следующих способов:
1) Если среди коэффициентов ряда 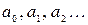 нет равных нулю, т.е. ряд содержит все целые положительные степени разности
нет равных нулю, т.е. ряд содержит все целые положительные степени разности 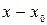 , то для вычисления радиуса сходимости
, то для вычисления радиуса сходимости 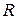 степенного ряда можно применять формулы:
степенного ряда можно применять формулы:
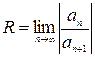 (8)
(8)
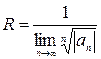 (9)
(9)
2) Во всех случаях интервал сходимости можно находить, применяя непосредственно признак Даламбера или признак Коши к ряду, составленному из абсолютных величин членов исходного ряда, т.е. к ряду
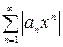 или
или 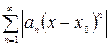
.
Пример 10.Найти область сходимости ряда 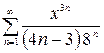 .
.
Решение. Так как среди коэффициентов ряда есть нулевые, то найдем интервал сходимости, применяя признак Даламбера к ряду, составленному из абсолютных величин членов исходного ряда, т.е к ряду
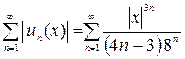 .
.
Имеем:
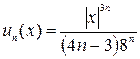 ;
; 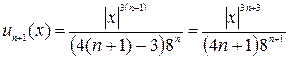 ;
;
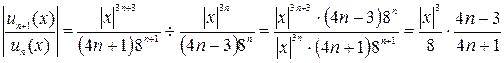 .
.
Тогда
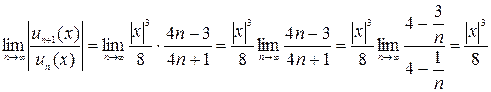 .
.
По признаку Даламбера ряд сходится, если 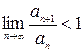 . Значит, интервалом абсолютной сходимости данного ряда будет интервал:
. Значит, интервалом абсолютной сходимости данного ряда будет интервал:
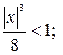
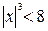 ;
;
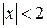 ;
;
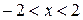 .
.
Исследуем сходимость ряда на концах интервала.
При 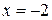 , получим числовой ряд
, получим числовой ряд
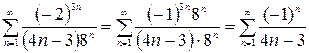 .
.
1. Исследуем ряд 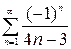 на абсолютную сходимость. Для этогоисследуем на сходимость ряд, составленный из абсолютных величин членов данного ряда:
на абсолютную сходимость. Для этогоисследуем на сходимость ряд, составленный из абсолютных величин членов данного ряда:
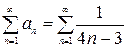 .
.
Сравним его с гармоническим рядом 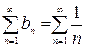 , который расходится.
, который расходится.
Так как
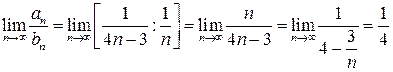 ,
,
т.е. 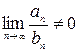 . Следовательно, на основании второго признака сравнения ряд
. Следовательно, на основании второго признака сравнения ряд 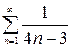 также расходится.
также расходится.
Следовательно, исходный ряд не является абсолютно сходящимся.
2. Используя признак Лейбница, исследуем ряд 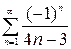 на условную сходимость. Для этого проверим условия (4):
на условную сходимость. Для этого проверим условия (4):
1) 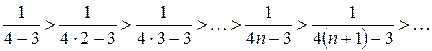
Очевидно, что данное неравенство верно для любого 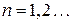
2) 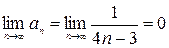 .
.
Таким образом, для данного знакочередующегося ряда выполняются условия признака Лейбница, откуда следует, что исходный ряд сходится условно.
При 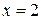 получим ряд
получим ряд
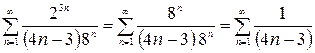 ,
,
расходимость которого доказана выше.
Следовательно, 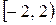 – область сходимости ряда;
– область сходимости ряда;
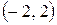 – область абсолютной сходимости ряда.
– область абсолютной сходимости ряда.
Пример 11. Найти область сходимости ряда 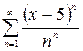 .
.
Решение. Так как ряд содержит все целые положительные степени разности 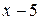 и все коэффициенты ряда содержатся в степени
и все коэффициенты ряда содержатся в степени 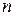 , то для вычисления радиуса сходимости
, то для вычисления радиуса сходимости 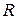 степенного ряда воспользуемся формулой (9).
степенного ряда воспользуемся формулой (9).
Так как 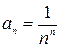 , то согласно формуле (9) находим
, то согласно формуле (9) находим
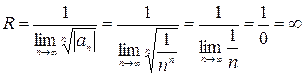 .
.
Таким образом, исследуемый ряд сходится абсолютно на всей числовой оси.
Ряды Тейлора
Мы рассматривали степенные ряды вида
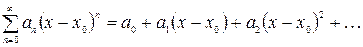
или
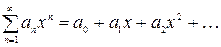
Каждый из таких рядов в своей области сходимости сходится к некоторой функции, сумме степенного ряда. Для приложений важно уметь данную функцию 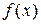 разлагать в степенной ряд, т.е. функцию
разлагать в степенной ряд, т.е. функцию 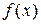 представлять в виде суммы степенного ряда.
представлять в виде суммы степенного ряда.
Как известно, для любой функции 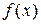 , определённой в окрестности точки
, определённой в окрестности точки 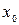 и имеющей в ней производные до
и имеющей в ней производные до 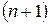 -го порядка включительно, справедлива формула Тейлора:
-го порядка включительно, справедлива формула Тейлора:
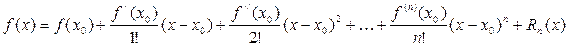 , (10)
, (10)
где 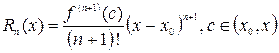 – остаточный член в форме Лагранжа. Число
– остаточный член в форме Лагранжа. Число 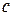 можно записать в виде
можно записать в виде 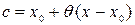 , где
, где 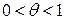 .
.
Формулу (10) кратко можно записать в виде
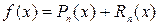 ,
,
где 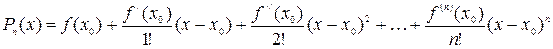 – многочлен Тейлора.
– многочлен Тейлора.
Если функция 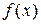 имеет производные любых порядков ( т.е. бесконечно дифференцируема ) в окрестности точки
имеет производные любых порядков ( т.е. бесконечно дифференцируема ) в окрестности точки 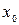 , то в формуле Тейлора мы можем использовать сколь угодно много членов. Тогда формула (10) примет вид:
, то в формуле Тейлора мы можем использовать сколь угодно много членов. Тогда формула (10) примет вид:
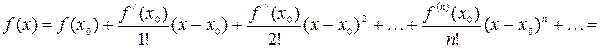
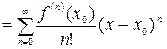 . (11)
. (11)
Определение. Ряд в разложении (11), называется рядом Тейлора для функции 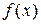 , а коэффициенты этого степенного ряда
, а коэффициенты этого степенного ряда
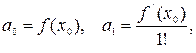
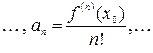
называются коэффициентами Тейлора.
Если в ряде Тейлора положить 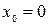 , то получим разложение функции по степеням
, то получим разложение функции по степеням 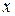 в так называемый ряд Маклорена:
в так называемый ряд Маклорена:
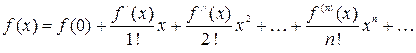
Замечание. В ряд Тейлора можно разложить любую бесконечно дифференцируемую в окрестности точки 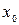 функции
функции 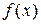 . Это является необходимым условием разложения функции
. Это является необходимым условием разложения функции 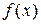 в ряд Тейлора. Но отсюда ещё не следует, что он будет сходиться к данной функции
в ряд Тейлора. Но отсюда ещё не следует, что он будет сходиться к данной функции 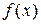 ; он может оказаться расходящимся или сходящимся, но не к функции
; он может оказаться расходящимся или сходящимся, но не к функции 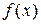 .
.
Теорема.Для того чтобы при некотором значении 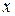 имело место разложение (11), необходимо и достаточно, чтобы при этом значении
имело место разложение (11), необходимо и достаточно, чтобы при этом значении 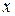 остаточный член формулы Тейлора (10) стремился к нулю при неограниченном возрастании
остаточный член формулы Тейлора (10) стремился к нулю при неограниченном возрастании 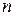 , т.е. чтобы
, т.е. чтобы
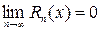 .
.
Способы разложения функции в ряд Тейлора
1. Непосредственное разложение
Для разложения функции 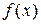 в ряд Тейлора нужно:
в ряд Тейлора нужно:
а) найти все производные до порядка 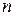 включительно:
включительно:
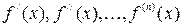 ;
;
б) вычислить значения производных в точке 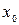 ;
;
в) составить ряд 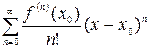 ;
;
г) найти радиус сходимости степенного ряда 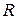 и интервал сходимости
и интервал сходимости 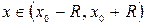 ;
;
д) доказать, что остаточный член ряда 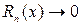 при
при 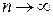 ,
, 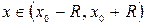 ;
;
е) Таким образом, 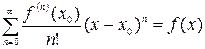 при
при 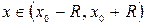 .
.
2. Косвенное разложение
В этом случае используют уже известные разложения и, применяя метод подстановки, получают разложения для других рядов.
Приведём разложения основных элементарных функций в ряд Маклорена:
1. 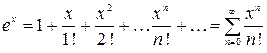 ,
, 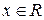 ;
;
2. 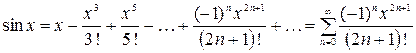 ,
, 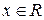 ;
;
3. 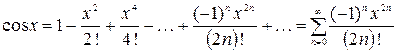 ,
, 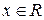 ;
;
4. 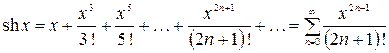 ,
, 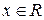 ;
;
5. 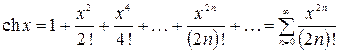 ,
, 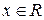 ;
;
6. 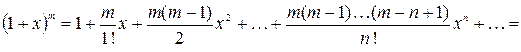
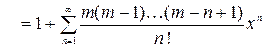 ,
, 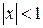 ;
;
В частности,
а) 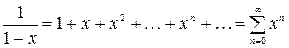 ;
;
б) 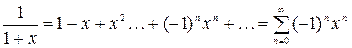 ;
;
7. 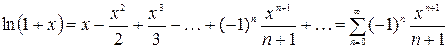 ,
, 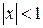 ;
;
8. 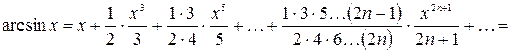
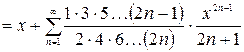 ,
, 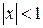 ;
;
9. 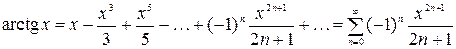 ,
, 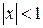 .
.
Пример 12.Разложить в ряд Маклорена функцию 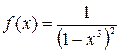 , пользуясь косвенным методом.
, пользуясь косвенным методом.
Решение. Заменяя 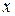 на
на 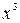 в разложении 6, получим:
в разложении 6, получим:
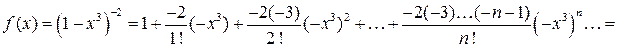
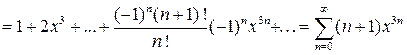 ,
, 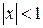 .
.
Пример 13.Разложить функцию 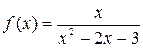 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 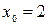 (по степеням
(по степеням  ).
).
Решение. Разложим функцию 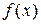 на сумму простейших дробей:
на сумму простейших дробей:
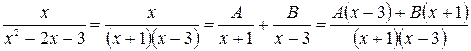 .
.
Найдём 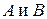 :
:
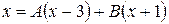
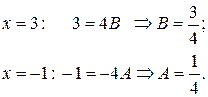
Таким образом,
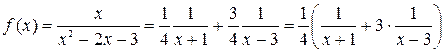 .
.
Разложим дроби 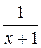 и
и 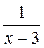 в ряд Тейлора по степеням
в ряд Тейлора по степеням  , используя разложения 6а) и 6б) :
, используя разложения 6а) и 6б) :
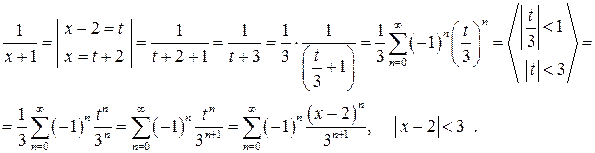
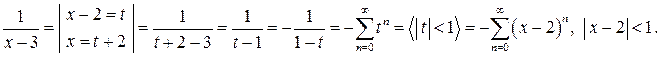 Следовательно, разложение функции
Следовательно, разложение функции 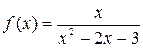 в ряд Тейлора по степеням
в ряд Тейлора по степеням 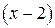 имеет вид:
имеет вид:
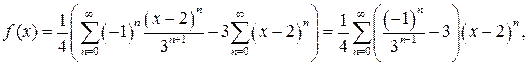 где
где
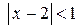 – интервал сходимости.
– интервал сходимости.
Дата добавления: 2017-04-20; просмотров: 12613;
