Примеры числовых рядов.

Пример 6.1. Исследуем на сходимость ряд

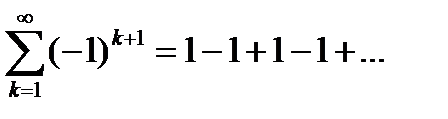. (6.13)

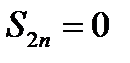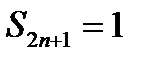Так как , а , то не существует 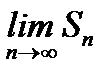. То есть ряд 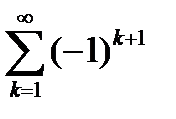расходится.

Ответ:Исходный ряд расходится.

Пример 6.2. Исследуем на сходимость ряд

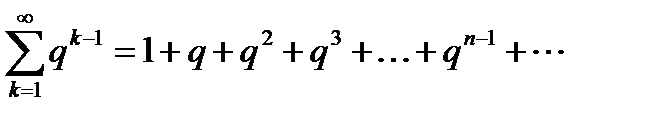, (6.14)

члены которого составляют геометрическую прогрессию со знаменателем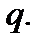

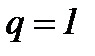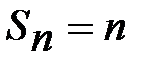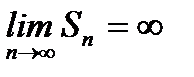1. Если , то , и ряд (6.14) расходится.

2. Если 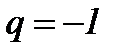, то ряд (6.14) совпадает с выше рассмотренным расходящимся рядом (6.13), то есть расходится.

3. Если 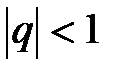, то

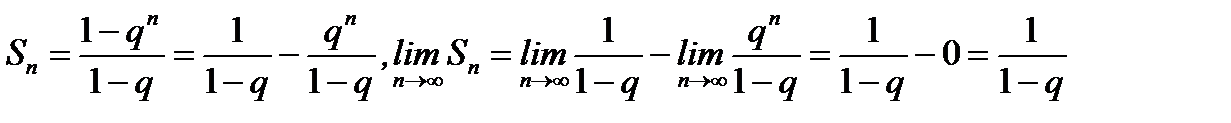
и, следовательно, исходный ряд (6.14) сходится, причем .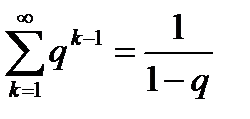

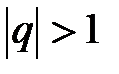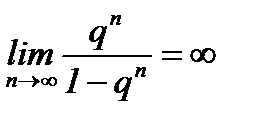4. Если , то и ряд (6.14) расходится.

Ответ: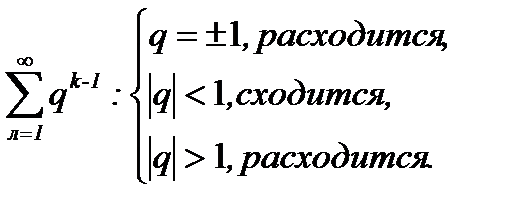

Пример 6.3. Пользуясь критерием Коши (см. теорему 6.1), исследуем на сходимость числовой ряд

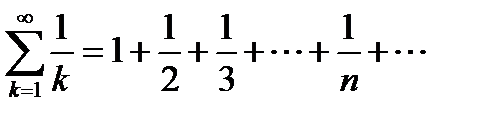, (6.15)

который в математике известен под названием гармонического ряда.

Заметим, что необходимое условие сходимости данного ряда выполняется, так как 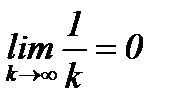. Докажем, однако, что этот ряд расходится. Для этого воспользуемся критерием Коши. А именно докажем, что, например, для 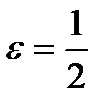не существует такого номера 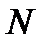, чтобы при 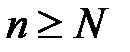и для 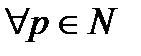имело бы место неравенство

.

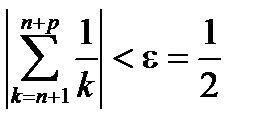На самом деле, например, при р = п имеем оценку

.

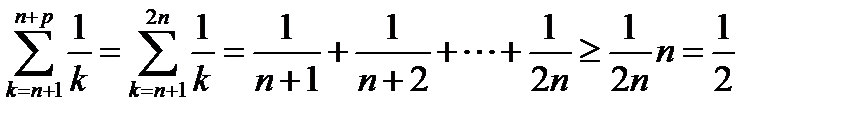Следовательно, в силу критерия Коши ряд (6.15) расходится.

Ответ:Гармонический ряд расходится.

Пример 6.4. Исследуем на сходимость ряд

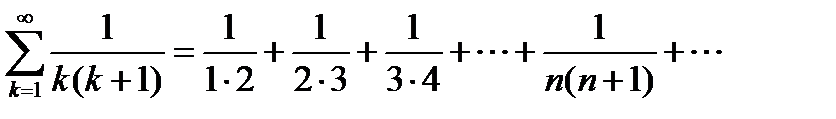. (6.16)

Пользуясь очевидным соотношением

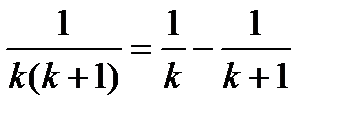(6.17)

п-ую частичную сумму 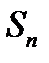данного ряда можно представить в виде

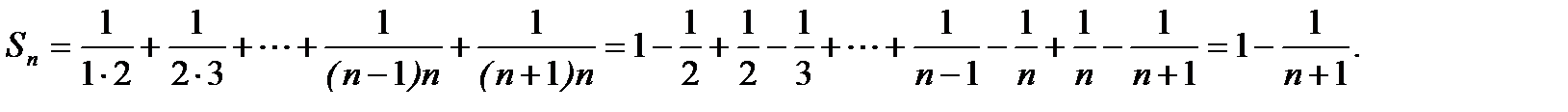
Тогда 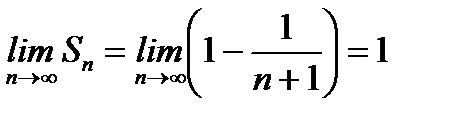и ряд (6.16) сходится, при этом .

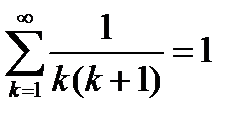Ответ:Исходный ряд сходится и сумма ряда равна единице.