Интервальный и дискретный вариационный ряд. Графическое представление статистических рядов.

Пусть имеется выборка значений некоторого признака X объёмом n = 50:

9,19 11,5 10,7 12,6 13,0 12,3 7,46 8,92 8,80 11,6 11,9 10,9 5,82 8,89 9,19 11,5 10,7 12,6 13,0 12,3 7,46 8,92 8,80 11,6 11,9 10,9 5,82 8,89 9,32 8,30 8,76 8,01 15,5 12,3 9,46 9,11 12,1 12,5 9,33 11,0 10,1 9,61 13,7 15,0 12,2 13,1 11,7 10,4 11,5 9,02 9,23 7,16 12,0 10,6 6,39 6,97 9,03 6,84 8,29 10,5 11,7 7,05 12,1 9,53

Требуется, разбивая её на k = 6 групп, составить:

1. интервальный вариационный ряд и построить гистограмму частот;

2. дискретный вариационный ряд и построить полигон частот.

Поступаем следующим образом.

1. Вводим данные в диапазон А1:А50, выделяем его и щелчком ЛКМ по кнопке располагаем варианты в порядке возрастания.

2. из полученного ряда находим значения minX = a1 = 5,82; maxX = a50 = 15,5. Их можно получить также встроенными функциями МИН и МАКС соответственно, диалоговое окно МИН показано на рис. 1:

Рис. 1

3. По формуле =a50-a1 находим размах выборки ΔX = 9,68

4. Оценивая шаг 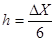, получаем 1,613333. Округляем (только в большую сторону) и принимаем h = 1,7

5. По формуле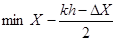

Оцениваем крайнее левое значение первого интервала, что даёт 5,56. округляем до 5,6 и убеждаемся, что так округлить можно: 5,6+6*1,7 = 15,8>15,5.

6. В диапазоне B1:B7 задаём арифметическую прогрессию, с первым членом 5,6 разностью (шагом) 1,7 предельным значением 15,8:

Рис. 2

7. С помощью встроенной функции СЧЕТЕСЛИ подсчитываем число вариантов, принадлежащих промежутку (5,6 7,3) и записываем результат в ячейку C1:

Рис. 3

Двойные кавычки в поле «Критерий» обязательны.

8. Аналогично подсчитываем и записываем в ячейку C2 число вариантов принадлежащих промежутку (5,6, 9]:

Рис. 4

Продолжая вычисления, приходим к последовательности (рис 5.)

Рис. 5

9. Вводим в ячейку D1 формулу =(B1+B2)/2 и, копированием её, задаём в диапазоне D1:D6 середины интервалов. В ячейку E1 вводим 6, а в ячейку E2 – формулу =C2-C1. Копируя её в ячейки E3:E6, получаем последовательность частот:

Рис. 6

Таким образом, интервальный вариационный ряд выборки записывается в виде

Граничное значение 10,7 отнесено к левому интервалу. Дискретный вариационный ряд задан в диапазоне D1:E6.

10. Графическим редактором «Мастер диаграмм» проводим построение гистограммы частот диапазона E1:E6

Рис. 7

Интервалы указываются на вкладке Ряд (подписи оси X):

Рис.8

11. Полигон частот строим командами Диаграмма ® Нестандартные ® Гистограмма | область:

Рис. 9

В командах Диаграмма ® Нестандартные ® Графики (2 оси) он имеет классический вид:

Рис. 10

Имеются и другие возможности геометрических представлений статистических распределений, включая построение в одной системе координат и полигона, и гистограммы, но на них останавливаться не будем.