Задания/примеры к практической части
1.
Путем проведения экспертного опроса и обработки его результатов методом непосредственной оценки упорядочить дисциплины, изучаемые во втором семестре 3-го курса, по убыванию сложности. Каждому эксперту парное сравнение дисциплин производить по 9-ти бальной шкале, используя степенную калибровку. Сопоставление каждой дисциплине ее численной оценки каждым экспертом произвести, используя модель равномерного сглаживания. Определить относительный коэффициент согласованности мнений экспертов с использованием распределения Стьюдента.
2.
Путем проведения экспертного опроса и обработки его результатов методом ранжирования упорядочить дисциплины, изучаемые во втором семестре 3-го курса, по убыванию сложности. Каждому эксперту произвести нестрогое ранжирование с выставлением стандартизированных рангов для эквивалентных, с точки зрения эксперта, альтернатив. Определить согласованность мнений экспертов и проверить статистическую значимость ранжировки при помощи коэффициента конкордации.
3.
Решение задачи линейного упорядочивания с использованием модели Ушакова для выбора одного из трех кандидатов на вакантную должность аналитика.
В результатеих парного сравнения получена матрица А. Затем матрицы Р = АТ и 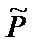 .
.
-  Þ
Þ 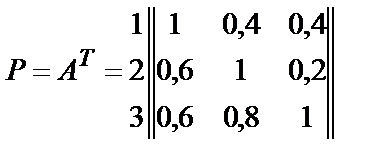 Þ
Þ  .
.
Для нахождения финальных вероятностей решим систему алгебраических уравнений
- 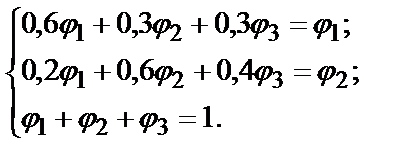
В результате решения системы уравнений получим:
- j 1 = 12/28, j 2 = 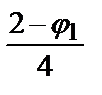 = 11/28, j 3 = 5/28.
= 11/28, j 3 = 5/28.
Следовательно, для замещения вакантной должности аналитика необходимо выбрать первую кандидатуру.
4.
Рассмотрим пример решения задачи линейного упорядочивания с использованием модели "спортивного" типа.
| 1 2 3 4 5 |
| 1 2 3 4 5 |
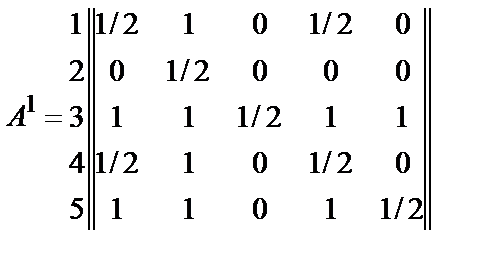

Вектор - столбцы для этих двух функций имеют вид
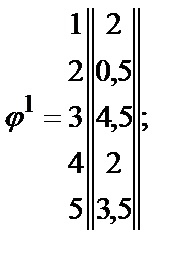
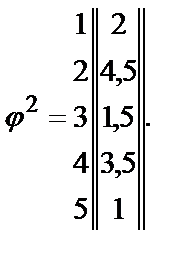
Если определить j = j 1 + j 2 , то можно получить вектор - столбец jТ, позволяющий упорядочить альтернативные варианты jТ = 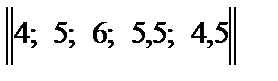 . Отсюда вывод, что функциональная клавиатура более предпочтительна для технического устройства, обеспечивающего диалог оператора АРМ с ЭВМ.
. Отсюда вывод, что функциональная клавиатура более предпочтительна для технического устройства, обеспечивающего диалог оператора АРМ с ЭВМ.
Пусть, например, был проведен экспертный опрос для выбора наиболее значимых параметров, определяющих качество корабельной ЭВМ. В процессе подготовки экспертизы были выявлены следующие параметры: емкость оперативной памяти, емкость памяти на сменных носителях, быстродействие, разрядность, наработка на отказ, среднее время восстановления, цена, обозначаемые в дальнейшем х1 – х7.
В результате ранжирования данных параметров 12 экспертами получена таблица 1.
Таблица 1.
Результаты ранжирования
| Эксперты | Параметры | ||||||
| х1 | х2 | х3 | x4 | x 5 | x 6 | х7 | |
| 5,5 | 5,5 | ||||||
| 6,5 | 6,5 | ||||||
| 5,5 | 5,5 | 2,5 | 2,5 | ||||
| 3,5 | 3,5 | ||||||
| 2,5 | 2,5 | ||||||
| 1,5 | 1,5 | ||||||
| 2,5 | 2,5 | ||||||
| 2,5 | 2,5 | ||||||
| 2,5 | 2,5 | ||||||
| Сумма рангов ri | 63,5 | 78,5 | 35,5 | 47,5 | |||
| Итоговый ранг |
Таким образом, наиболее важным параметром при выборе корабельной ЭВМ является обеспечение высокой безотказности, а наименее важным – наличие большой емкости памяти на сменных носителях (внешней памяти). Однако, т.к. при ранжировании используется шкала порядка, то нельзя сказать, насколько одна альтернатива предпочтительней другой.
5.
Пусть, например, десять экспертов с одинаковыми bk = 1 оценивают среднее время наработки на отказ радиотехнической аппаратуры корабельной АСУ. В результате оценки получены следующие значения Ti в часах: Т1 = 40; Т2 = 42; Т3 = 38; Т4 = 44; Т5 = 37; Т6 = 34; Т7 = 46; Т8 = 45; Т9 = 33; Т10 = 42.
Результирующая оценка, рассчитанная как среднее арифметическое данных 10 оценок:
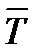 = 40,1 ч; s 2= 18,29 ч 2; s = 4,28 ч.
= 40,1 ч; s 2= 18,29 ч 2; s = 4,28 ч.
Задав уровень значимостиa = 0,05, по таблицам распределения Стьюдента определим значение t для числа степеней свободы m – 1 = 9. Тогда t = 2,26.
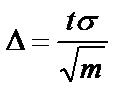 = 3,06 ч.
= 3,06 ч.
Таким образом: 37,04 < Т < 43,16 ч.
В данном примере относительный (нормализованный) коэффициент согласованности мнений экспертов меньше 0,1: 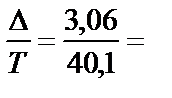 0,076 < 0,1.
0,076 < 0,1.
6.
Допустим, руководство предприятия должно выбрать вариант планового решения об уровне выпуска и реализации продукции с учётом конъюнктуры рынка:
| План производства и реализации продукции | Конъюнктура рынка | ||
| П1 | П2 | П3 | |
| Вероятности состояния спроса | |||
| q1 = 0,2 | q2 = 0,5 | q3 = 0,3 | |
| Размер прибыли аij , млн. ден.ед. | |||
| С1 | 7,2 | 8,7 | 6,5 |
| С2 | 8,8 | 7,3 | 9,4 |
| С3 | 6,4 | 5,4 | 7,4 |
Критерии выбора стратегии
Проведем анализ стратегий производства при неопределенной рыночной конъюнктуре. Для выбора наилучшей стратегии поведения на рынке товаров и услуг существуют различные критерии, среди которых можно назвать критерии: Байеса, Лапласа, Вальда, Сэвиджа, Гурвица и максимакса. Предпочтительнее будет выбрать то решение, которое будет оценено как наиболее полезное по нескольким критериям.
Критерий Байеса используется, если в результате исследований известны вероятности всех состояний Природы (qj). При этом, если учтены все из n возможных состояний, тогда
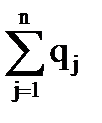 = 1.
= 1.
В этом случае в качестве показателя, который необходимо максимизировать, берется среднее значение выигрыша
B = 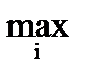
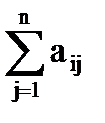 × qj.
× qj.
Определим наилучшую стратегию по критерию Байеса:
7,2 × 0,2 + 8,7 × 0,5 + 6,5 × 0,3 = 7,74 ,
8,8 × 0,2 + 7,3 × 0,5 + 9,4 × 0,3 = 8,23 ,
6,4 × 0,2 + 5,4 × 0,4 + 7,4 × 0,3 = 6,2.
Наилучшая стратегия С2 дает максимальный средний «выигрыш» в размере 8,23 млн. ден.ед.
Критерий Лапласа применяется в случае наибольшей неопределенности обстановки. При этом все n состояний Природы принимаются равновероятными, т.е. вероятность каждого из состояний qj = 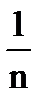 . Согласно этому критерию «недостаточного основания» находится максимальный «средний» выигрыш.
. Согласно этому критерию «недостаточного основания» находится максимальный «средний» выигрыш.
L = 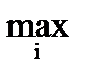
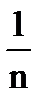
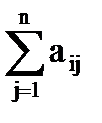 .
.
Определим наилучшую стратегию по критерию Лапласа:
(7,2 + 8,7 + 6,5) /4 = 7,5,
(8,8 + 7,3 + 9,4) /4 = 8,5,
(6,4 + 5,4 + 7,4) /4 = 6,4.
Наилучшая стратегия С2 дает максимальный средний «выигрыш» в размере 8,5 млн. ден.ед.
7.
Пример. Допустим, руководство предприятия рассматривает два альтернативных варианта решения (А1 и А2) при двух возможных сценариях (В1 и В2) развития ситуации во внешней среде. Оценки последствий решений в виде ожидаемой прибыли (в млн. ден.ед) представлены следующей матрицей игры
| В1 | В2 | |
| А1 | ||
| А2 |
Определим нижнюю a и верхнюю β цену игры:
| В1 | В2 | ai = minj aij | ||
| А1 | a = maxi ai | |||
| А2 | ||||
| βj = maxi aij | ||||
| β = minj βj | a ¹ β |
Поскольку нижняя цена игры не равняется верхней, игра решается в смешанных стратегиях.
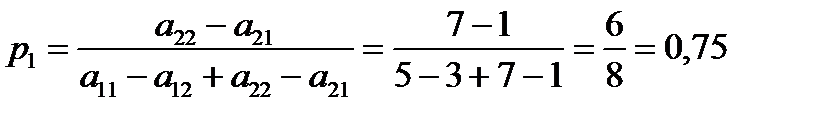 ,
,
р2 = 1 – р1 = 1 – 0,75 = 0,25
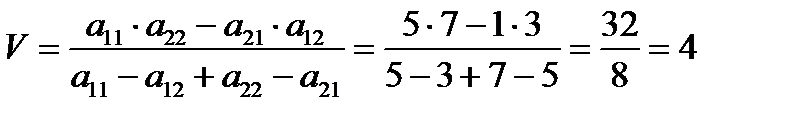 .
.
Таким образом, для получения гарантированной прибыли, равной 4 млн. ден.ед., необходимо чередовать возможные решения с частотой ( вероятностью) 0,75 для С1 и 0,25 для С2. Или распределить свои ресурсы между решениями С1 и С2 в пропорции 3:1 (0,75:0,25 = 3:1).
8.
Задача. Партию товара, затраты на которую составили 200 ден.ед., фирма планирует продать с прибылью. Однако существует риск, что слишком высокая продажная цена замедлит, а то и вовсе остановит реализацию товара, и фирма вместо прибыли получит одни убытки. По мнению экспертов фирмы, вероятность продажи товара по цене выше 400 ден. ед. вообще равна нулю.
В то же время снижение продажной цены ради ускорения процесса реализации тоже должно иметь какие-то разумные пределы. Продажа данной партии товара, например по цене ниже 200 ден. ед., приносит фирме прямые убытки.
Определить оптимальный уровень продажной цены за данную партию товара на предстоящих торгах.
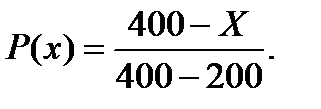 Решение. Поскольку продавать данный товар по цене ниже 200 ден. ед. не выгодно, а по цене выше 400 ден. ед. невозможно, определим вероятность продажи всей партии товара по цене Х в интервале 200-400 ден. ед. Это можно сделать по формуле
Решение. Поскольку продавать данный товар по цене ниже 200 ден. ед. не выгодно, а по цене выше 400 ден. ед. невозможно, определим вероятность продажи всей партии товара по цене Х в интервале 200-400 ден. ед. Это можно сделать по формуле
Вероятность же того, что вся партия может оказаться непроданной, найдем как Q(x) = 1 – P(x).
Величины P(x) и Q(x) можно трактовать не только как вероятности, но и как доли проданной и непроданной продукции.
Возможную прибыль от реализации всей партии по цене Х определим как Х – 200.
Проделав с помощью приведенных формул соответствующие расчеты, получим следующую таблицу.
| Запрашиваемая цена (х) | Вероятность того, что партия будет | Размер прибыли, ден. ед. | |
| продана Р(х) | не продана Q(х) | ||
| 0,75 | 0,25 | ||
| 0,5 | 0,5 | ||
| 0,25 | 0,75 | ||
На основе этих данных построим дерево решений и с его помощью найдем оптимальное решение, касающееся уровня запрашиваемой цены на предстоящих торгах.
Дерево решений изображено на рис. 1. Пункт принятия решений на нем обозначен квадратом. Из него выходят пять дуг (ветвей), соответствующих пяти вариантам запрашиваемой цены: 200, 250 и т. д. На концах выходящих из квадратной вершины ветвей стоят круглые вершины, изображающие узлы возникновения неопределенностей (поскольку, приняв то или иное решение, мы еще не знаем, что оно нам даст).
Из каждого узла неопределенности выходят по две ветви, соответствующие двум возможным исходам: товар будет продан (П) и товар не будет продан (Н). Возле каждой ветви проставляются соответствующие вероятности. На самых концах финальных ветвей проставляется ожидаемая прибыль или убытки от того, что партия товара будет продана или не будет.
| 2 0 0 -50 0,75 50 0,25 -50 0,5 100 0,5 -50 0,25 150 0,75 -50 2 200 3 -50 |
| 0 0 |
| -50 |
Рис. 1. Дерево решений по определению цены продажи
Величину убытков для всех вариантов решений примем условно на уровне 25 % от затрат, допустив, что товар обесценится на четверть, если не будет продан на ближайших торгах. В каждой реальной ситуации их находят, сообразуясь с конкретными обстоятельствами.
После построения дерева решений начинается его обратный анализ. Идя по ветвям дерева справа налево и попадая в круглые вершины, проставим рядом с ними математические ожидания прибыли, которая рассчитывается следующим образом:
М(х1) = 0 * 1 – 50 * 0 = 0,
М(х2) = 50 * 0,75 – 50 * 0,25 = 25,
М(х3) = 100 * 0,5 – 50 * 0,5 = 25,
М(х4) = 150 * 0,25 – 50 * 0,75 = 0,
М(х5) = 200 * 0 – 50 * 1 = -50.
Двигаясь далее влево, дойдем до квадратной вершины – узла принятия решения, рядом с которым проставим максимальную величину из тех, что стоят на концах выходящих из него ветвей. В нашей задаче таких величин две (обе равны 25) и они соответствуют решениям о назначении цены продаж на уровне 250 и 300.
Для принятия окончательного решения необходимо проверить, нет ли между двумя наибольшими значениями результатов третьего, с еще большим значением прибыли. Сделаем проверку для цены в 275 ден. ед.:
Р(275) = (400-275)/(400-200) = 0,625 , Q(275) = 1-0,625 = 0,375 ,
прибыль составит 275 – 200 = 75, убытки равны 50.
Отсюда М(275) = 75 * 0,625 – 50 * 0,375 = 28,125.
Таким образом, приняв решение о цене продажи в 275 ден. ед., можно обеспечить более высокий результат, чем при ценах в 250 или 300 ден. ед.
Для уточнения сделаем еще одну проверку в окрестностях цены, равной 275 ден. ед., и найдем, что отклонения от нее как в большую, так и в меньшую сторону снижают ожидаемую прибыль. Так, для цен в 270 и 280 ден. ед. прибыль получится равной 28 ден. ед.
Значит, окончательное оптимальное решение – остановиться на цене в 275 ден. ед.
Возможно построение с самого начала более подробной модели дерева решений с более мелким шагом изменения цены продаж, например в 25 или 5 ден. ед. Тогда оптимальное решение было бы получено сразу, без дополнительных проверок. Однако в таком случае само дерево оказалось бы более громоздким, что дало бы менее экономичный путь нахождения оптимального решения. Поэтому целесообразнее строить дерево с более крупным шагом, а потом провести проверку в нужном месте с более мелкой градацией цены продаж.
Дата добавления: 2018-06-28; просмотров: 543;
