Основные принципы метода анализа иерархий

1. Принцип идентичности и декомпозиции.Предусматривает структурирование проблем в виде иерархии или сети.

2. Принцип сравнительный суждений (парных сравнений). Предполагает, что элементы задачи (альтернативы и критерии) сравниваются попарно с позиции их воздействия на общую характеристику.

3. Принцип синтеза приоритетов. Предполагает формирование набора локальных приоритетов, которые выражают относительное влияние множества элементов на элемент примыкающего сверху уровня.

Этапы МАИ

Этап 1.Построение иерархической структуры задачи многомерного выбора.

В общем случае простейшей трехуровневой иерархии структура имеет вид Рис.1

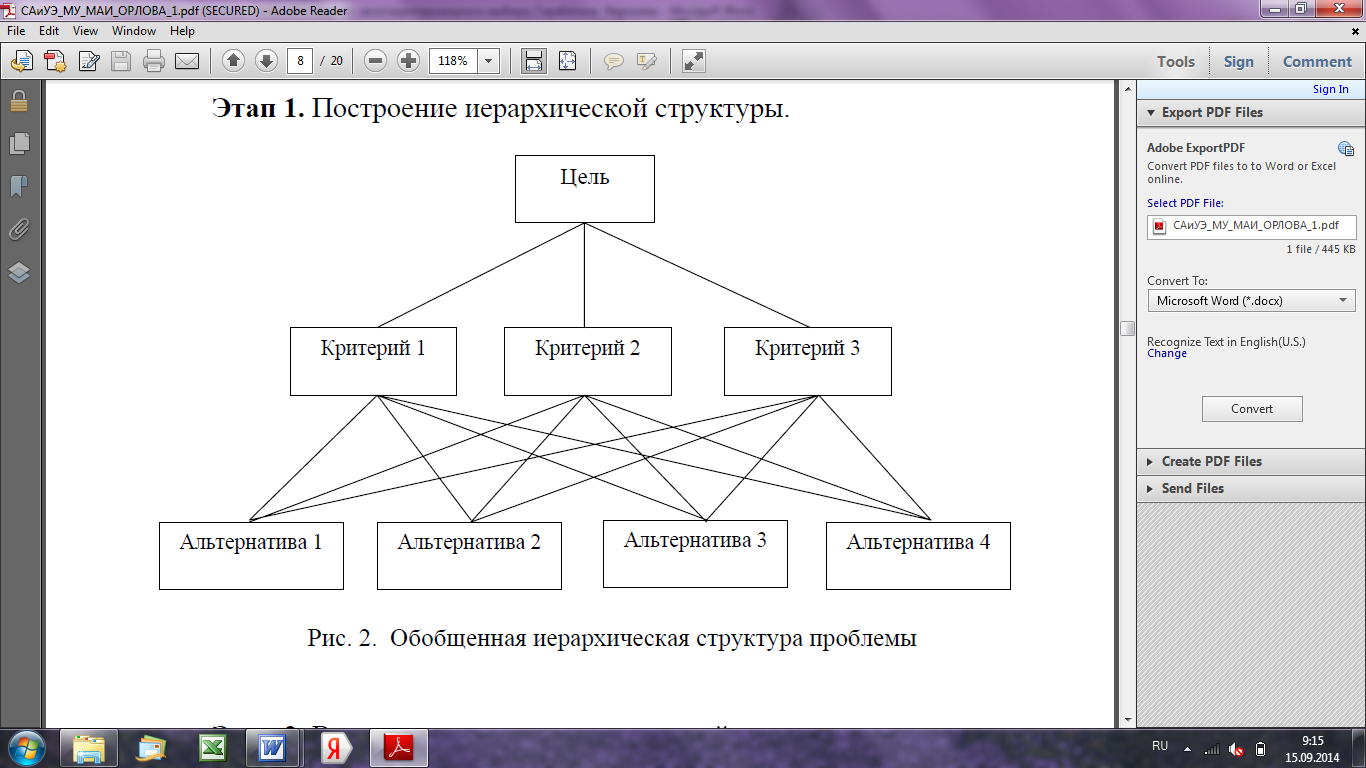
Рис. 1. Обобщенна иерархическая структура проблемы

Этап 1.Структуризация.

Структуру решаемой задачи можно представить в виде иерархической структуры, показанной на Рис. 2.

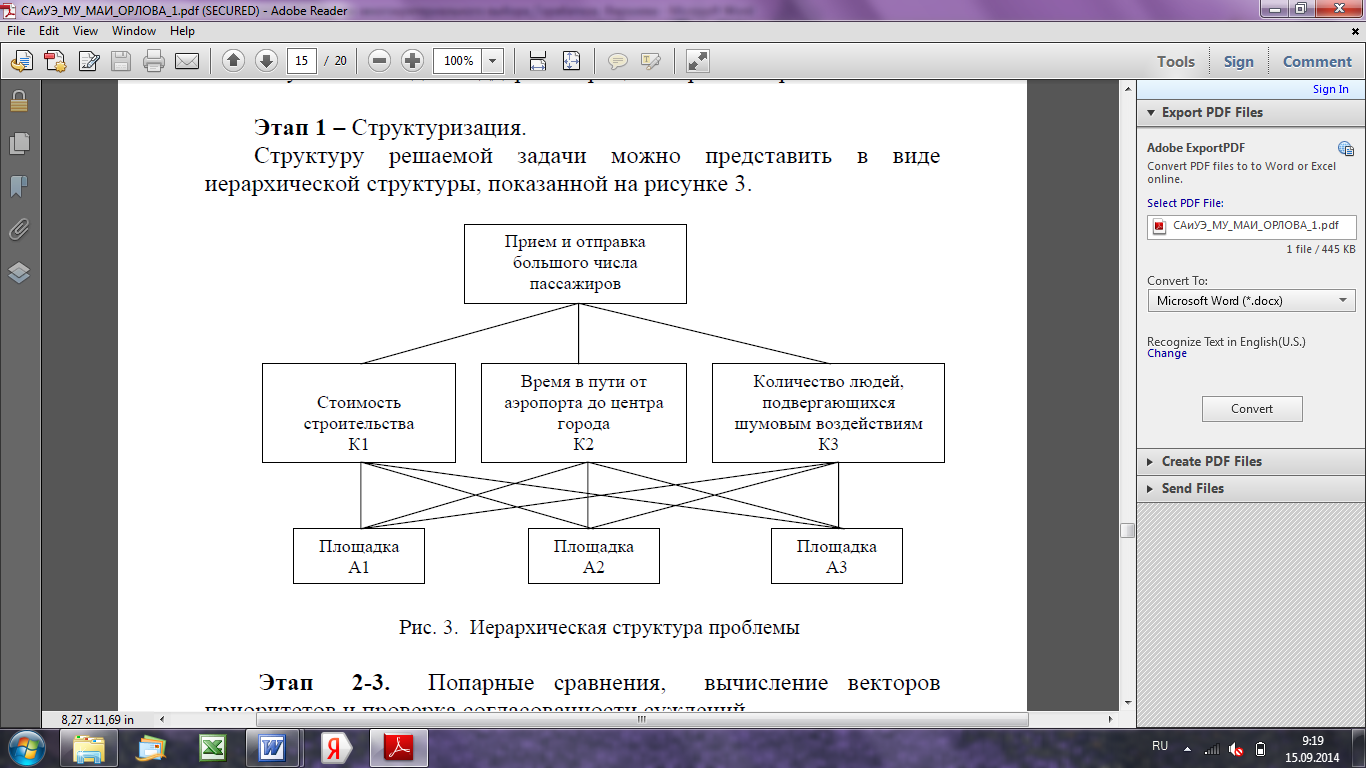
Рис. 2. Иерархическая структура проблемы

Этап 2.Выполнение попарных экспертных сравнений элементов каждого уровня иерархий.

Рассмотрим элементы С₁, С₂, …, С_n некоторого зафиксированного уровня иерархи. Мы хотим определить веса ѡ₁, ѡ₂, …,ѡ_n влияния этих элементов на некоторый элемент вышестоящего уровня. Основным инструментом оценки влияния является матрица чисел по шкале отношений 1, …, 9 (табл. 1), представляющих суждения о парных сравнениях. Для представления приоритетов в МАИ выбран собственный вектор, принадлежащий наибольшему собственному значению указанной матрицы А. Обозначим через 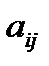число (бал), соответствующее значимости (предпочтения) элемента С_i по сравнению с элементом С_j данного уровня иерархии по влиянию С_i, С_j на фиксированный элемент вышестоящего уровня (например К1 на Рис. 2):

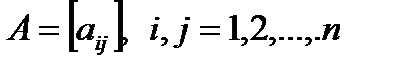. (4)

Матрица А с содержательной точки зрения будет согласованной по оценкам при введении условия

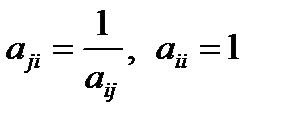. (5)

С математической точки зрения это условие наделяет матрицу А свойством обратносимметричной матрицы. На главой диагонали матрицы А стоят 1.

Если оценки попарных сравнений известны точно, т.е. основаны на экспериментальных измерениях, то

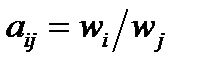, (6)

т.е. веса влияния элементов известны.

Например, если взвешиваются два предмета: С₁=3052 и С₂=2442. Тогда отношение 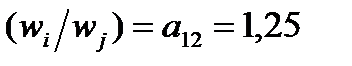означает, что предмет С₁ в 1,25 раз тяжелее предмета С₂.

Этап 3. Определение вектора приоритетов.

В качестве вектора приоритетов для каждого уровня иерархии принят нормализованный главный собственный вектор матрицы попарных сравнений.

Этап 4. Определение максимальных собственных значений и степени согласованности матриц парных сравнений.

Прежде чем перейти к синтезу оптимальной альтернативы с учетом всех элементов второго и третьего уровней иерархии, нужно убедиться в достаточном уровне согласованности всех матриц суждений А_с.1, А_с.2, А_с.2, А_с.4. Для этого нужно вычислить максимальные собственные значения 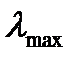этих матриц.

Этап 5. Определение индексов согласованности и отношений согласованности для матриц суждений.

В общем случае под согласованностью понимается то, что при наличии основного (базового) массива необработанных данных все другие данные логически могут быть получены из них. Или другими словами, отношения элементов всей матрицы А не должны быть противоречивыми.

Этап 6. Синтез приоритетов уровней.

В математической теории иерархий разработан метод оценки воздействия уровня на соседний вышестоящий уровень путем композиции соответствующего вклада (приоритетов) элементов данного уровня по отношении к каждому элементу соседнего верхнего уровня. Композиция распространяется снизу-вверх. В принципе, можно рассматривать также распространение композиции сверху-вниз.

Этап 7. Выбор оптимально альтернативы.

Алгоритм оптимального выбора прост:

.

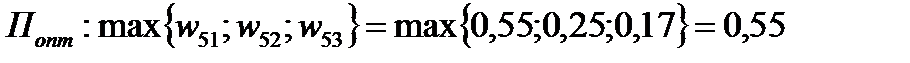Таким образом, алгоритм оптимального многокритериального выбора приводит к выбору площадки П₁ для строительства аэропорта, так как ей соответствует наибольшее значение компоненты вектора общего приоритета

.

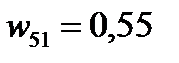Достоинством метода анализа иерархий является направленность на сравнение реальных альтернатив. Метод может применятся в тех случаях, когда эксперты не могут дать абсолютной оценки альтернатив по критериям, а пользуются более слабыми сравнительными измерениями.