Операции, выполняемые над нечеткими множествами
1. Проверка тождества нечетких множеств. Два нечетких множества А и В равны (тождественны), если степень принадлежности любого элемента (х Î Х) нечеткому множеству А равна степени его принадлежности нечеткому множеству В:
(А = В) Û (mА(х) = mВ(х)),"х Î Х .
2. Включение нечетких множеств. Множество А включено в множество В, если степень принадлежности любого элемента (х Î Х) нечеткому множеству А меньше или равна степени его принадлежности нечеткому множеству В:
(А Ì В) Û (mА(х) £ mВ(х)),"х Î Х .
3. Пересечение нечетких множеств. Пересечением нечетких множеств А и В является нечеткое множество (АÇВ), которому любой элемент (х Î Х) принадлежит со степенью принадлежности mАÇВ (х), определяемой соотношением:
(АÇВ) Û mАÇВ(х) = min{(mА(х), mВ(х)},"х Î Х .
4. Объединение нечетких множеств. Объединением нечетких множеств А и Вявляется такое нечеткое множество (АÈВ), которому любой элемент (х Î Х) принадлежит со степенью принадлежности mАÈВ (х), определяемой соотношением:
(АÈВ) Û mАÈВ(х) = max{(mА(х), mВ(х)},"х Î Х .
5. Дополнение нечетких множеств. Дополнением нечеткого множества А является такое нечеткое множество (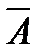 
), которому любой элемент (х Î Х) принадлежит со степенью принадлежности 
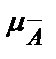(х), определяемой соотношением:
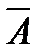( ) Û 
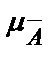(х)=1 – mА(х), "х Î Х .
6. Алгебраическое произведение нечетких множеств. Алгебраическим произведением нечетких множеств А и В является такое нечеткое множество (АВ), которому любой элемент (х Î Х) принадлежит со степенью принадлежности mАВ (х), определяемой соотношением:
(АВ) Û mАВ(х) = (mА(х)×mВ(х),"х Î Х .
7. Алгебраическая сумма нечетких множеств. Алгебраической суммой нечетких множеств А и В является такое нечеткое множество (АÅВ), которому любой элемент (х Î Х) принадлежит со степенью принадлежности mАÅВ (х), определяемой соотношением:
(АÅВ) Û mАÅВ(х) = mА(х) + mВ(х) – (mА(х)×mВ(х),"х Î Х .
Дата добавления: 2018-06-28; просмотров: 547;