ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
Множеством называется совокупность некоторых объектов, объединенных общим признаком.
Для множеств вводятся следующие отношения.
Множество А нестрого включено в множество В (обозначается АÍВ) если для любого элемента хÎА, следует что хÎB. Нестрогое включение не исключает совпадения множеств.
Множество А строго включено в множество В (обозначается АÌВ) если:
1) АÍВ;
2) существует yÎB, такой, что yÏA.
Множество А совпадает с множеством В (А = В), если все элементы множества В являются элементами множества В и все элементы множества В являются элементами множества А, т.е.
(АÍВ и ВÍА) Û (А = В).
Большинство утверждений теории множеств связано с равенством двух множеств и включением одного множества в другое. Поэтому детально разберёмся в методах доказательства этих фактов.
1. Доказательство нестрогого включения АÍВ. Для этого нужно доказать, что любой элемент x, принадлежащий множеству А одновременно является элементом множества В, т.е.
(" x Î А) Þ (x Î В).
2. Доказательство строгого включения АÌВ состоит из двух частей:
1) АÍВ;
2) $ y: y Î B и y Ï A.
3. Доказательство равенства А = В сводится к доказательству двух включений А Í В и В Í А.
Дадим определения операций над множествами, используя способ задания множества характеристическим свойством или формулой теории множеств.
1. Дополнение 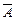 :
: 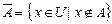 .
.
2. Пересечение 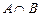 :
: 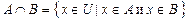 .
.
3. Объединение 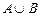 :
: 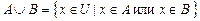 .
.
4. Разность 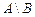 :
: 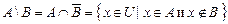 .
.
5. Симметрическая разность 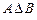 :
: 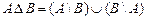 .
.
В доказательствах будем также использовать следующие краткие обозначения, для того чтобы расписать принадлежность элемента множеству, построенному с помощью операций над множествами.
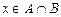 Û
Û 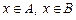 Û
Û 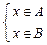
Фигурная скобка и запятая здесь, как и прежде, обозначает выполнение обоих свойств.
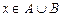 Û
Û 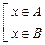
Квадратная скобка означает выполнение хотя бы одного из свойств. Таким образом, доказательство в дальнейшем распадается на два случая, для которых рассуждения проводятся отдельно, каждое в своей строке.
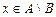 Û
Û 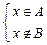
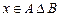 Û
Û 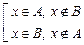
Распишем также, что означает, что элемент не принадлежит множеству, построенному с помощью операций над множествами.
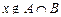 Û
Û 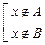
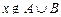 Û
Û 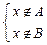
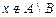 Û
Û 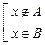
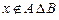 Û
Û 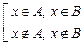
Если из условия следует свойство о принадлежности элемента одному множества (например 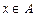 ) и ничего не известно относительно другого (B), которое участвует в формуле доказываемого утверждения, то необходимо рассмотреть оба случая
) и ничего не известно относительно другого (B), которое участвует в формуле доказываемого утверждения, то необходимо рассмотреть оба случая 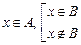 и в обоих случаях вывести (или опровергнуть) требуемое свойство.
и в обоих случаях вывести (или опровергнуть) требуемое свойство.
Утверждение вида 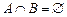 эквивалентно включениям
эквивалентно включениям 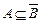 или
или 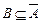 .
.
Дата добавления: 2017-02-20; просмотров: 719;
