Теоретические сведения

Введем следующие обозначения

.

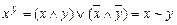Легко проверить, что , .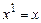

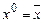Теорема 1.(о разложении булевых функций). Любую булеву функцию можно представить в виде

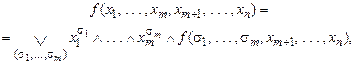(5.1)

где дизъюнкции берутся по всем возможным наборам ( ).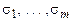

Теорема 2. Всякая булева функция (кроме 0) имеет единственную СДН-форму

.

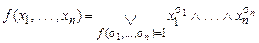С помощью принципа двойственности легко доказать представление функции СКН-формой.

Теорема 3. Всякая булева функция (кроме 1) имеет единственную СКН-форму

.

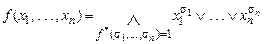С помощью совершенных нормальных форм можно решить проблему выполнимости или опровержимости формулы.

Для того чтобы найти, при каких значениях высказывательных переменных формула является выполнимой, необходимо построить ее СДН-форму. Количество таких наборов равно числу полных элементарных конъюнкций, так как, если одна из них истинна, то истинна и вся формула. Элементарная конъюнкция истинна, когда истинны все её составляющие, следовательно, если переменная входит в неё без отрицания, то она принимает значение 1, а если с отрицанием, то – 0. Аналогично, для решения задачи опровержимости строится СКН-форма.

Совершенные нормальные формы используются также для решения задачи, обратной задаче разрешимости – построение реализации булевой функции, заданной таблицей. Нули функции определяют полные элементарные дизъюнкции, входящие в СКН-форму функции. Такая дизъюнкция строится так, чтобы все составляющие ее переменные или их отрицания обращались в нуль, т.е. если значение переменной 0, то переменная входит в дизъюнкцию без отрицания, если – 1, то – с отрицанием. Соответственно, по единицам булевой функции можно построить ее СДН-форму.

Для вычисления значений булевых функций в общем случае надо использовать сложную рекурсивную процедуру (см. [3], п. 3.2.1.), т.к. надо определить все подформулы вплоть до Х_i или 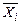. При использовании совершенных форм алгоритм вычисления будет намного проще и эффективнее.

В ЭВМ совершенные формы представляются в виде матрицы размера k´n, состоящей из нулей и единиц, где k – число членов разложения (элементарных конъюнкций или дизъюнкций); n – число пропозиционных переменных. Матрица F представляет собой часть общей таблицы истинности, определяющей булеву функцию f. Для представления СДНФ берутся строки, соответствующие единицам f, а для СКНФ – строки, соответствующие нулям f.

Пусть х – массив пропозиционных переменных. Предположим, х_i получили некоторые значения и необходимо вычислить значение нормальной формы f. Предлагаются следующие правила:

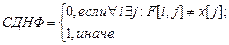
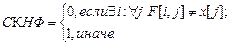
Эффективность данного алгоритма проявляется также в том, что цикл можно прервать, как только будет найдено необходимое значение i или j.

Например, вычислим значение функции f(x₁, x₂) = x₁ ~ x₂ при x₁ = 0; x₂ = 1. Запишем таблицу истинности функции f:

Тогда F_СДНФ = 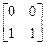; F_СКНФ = 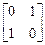. Поскольку ни одна из строк F_СДНФ, которая определяет наборы значений переменных, соответствующие 1 функции, не совпала с заданными значениями х_j, то f (0, 1) = 0.

Тоже самое можно определить и по СКНФ, так как первая строка F_СКНФ совпадает со значениями х_j, то f (0, 1) = 0.

Сформулируем законы булевой алгебры и производные от них формулы в терминах булевых функций.

1. X ÙY º Y ÙX, X ÚY º YÚX.

2. (X ÙY)ÙZ º X Ù(YÙZ), (XÚY)ÚZ º XÚ(YÚZ).

3. XÙX º X, XÚX º X.

4. XÚ(X 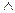Y) º X, X 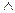(XÚY) º X.

5. X Ù(YÚZ) º (X ÙY)Ú(X ÙZ), XÚ (YÙZ) º (XÚY)Ù(XÚZ).

6. XÙ0 º Л, XÙ1 º X,

XÚ0 º X, XÚ1 º 1.

7. , .

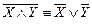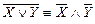8. .

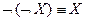9. 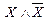º 0.

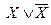10. º 1.

11. .

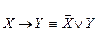12. .

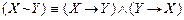13. ,

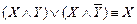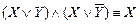
14. ,

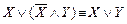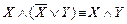
Для преобразования одной совершенной нормальной формы в другую нужно вначале максимально упростить исходную форму, воспользовавшись законами 4, 5, 13, 14. Затем преобразовать упрощенную формулу по свойству взаимной дистрибутивности 5, получив нормальную форму, и развернуть её в требуемую совершенную форму по законам склеивания 13.