Технология выполнения работы.

Рассмотрим возможные подходы к построению программы и используемым типам данных.

1. Множество X,на котором задано бинарное отношение, можно определить статическим одномерным массивом, количество элементов множества – символьной константой. Например,

const int n=5; int X []={1, 2, 3, 4, 5};

Тогда матрица бинарного отношения и матрица срезов элементов могут быть определены как двумерные статические массивы.

Недостатками такого подхода является то, что при изменении исходного множества требуется повторное построение программы, и то, что в строках матрицы срезов будут присутствовать незаполненные ячейки. Количество элементов срезов нужно будет запоминать в одномерном массиве.

2. Избавиться от первого недостатка предыдущего подхода можно, используя динамические массивы для исходного множества и матриц бинарного отношения и срезов. Элементы исходного множества в этом случае можно будет вводить с консоли или из файла, причем количество элементов множества в этом случае является переменным и может быть определено программно.

Однако определение матрицы срезов динамическим массивом не избавляет программу от второго недостатка – использование лишней памяти.

3. Эффективного использования памяти можно достичь, используя контейнерный класс – вектор. Предварительно определение контейнерного класса vector должно быть подключено к тексту программы.

Тип элементов вектора задаётся при описании переменной этого типа. Например, исходное множество X вариантов задания описывается как

vector <int> X ;

Матрица в этом случае определяется как вектор, составленный из векторов. Для краткости и лучшей читаемости программы можно предварительно определить соответствующие типы для множества элементов и матрицы.

typedef vector <int> i_set;

typedef vector <vector <int>> matrix;

Так как размер матрицы бинарного отношения n определён после ввода множества, на котором задано отношение, то можно выделить для неё память и инициализировать элементы матрицы

с помощью инструкций

matrix R(n);

for (i=0; i<n; i++) R[i].resize(n);

Таким образом, выделяется память под n векторов, размерность каждого из которых n, а элементы векторов заполнятся нулями.

В основной программе строится и печатается матрица бинарного отношения (печать матрицы можно оформить в виде функции). Передача матрицы функции в качестве параметра в этом случае осуществляется через ссылку (matrix&).

Затем по матрице бинарного отношения для каждого элемента множества X строиться срез этого элемента, заданный в варианте. Верхние или нижние срезы элементов следует сохранить в соответствующей матрице срезов. Если для представления матрицы используется тип matrix, то для объявления переменной воспользуемся конструктором с инициализацией (например, matrix Gs(n);), который выделит память под n пустых векторов. Заполнение соответствующего вектора будет выполняться при построении среза заданного элемента, причем количество элементов в векторе равно числу элементов в соответствующем срезе.

Построение матрицы срезов оформить в виде функции. Параметрами такой функции должны быть множество, на котором определено бинарное отношение, матрица бинарного отношения и матрица, строящегося верхнего или нижнего среза. Например, объявление функции, строящей верхний срез по матрице бинарного отношения R имеет вид

void v_srez (int* X, matrix& R, matrix& G);

В теле функции необходимо проверить каждую строку (для нижних срезов) или каждый столбец (для верхних срезов) матрицы бинарного отношения. Если элемент матрицы равен 1, то в строку матрицы срезов необходимо записать соответствующий элемент множества X в конец вектора 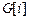(i – номер элемента, для которого строится срез) с помощью функции 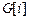.push_back(el). Количество записанных в вектор элементов можно получить с помощью функции 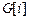.size().

На печать или в файл нужно вывести срезы элементов, указанных в варианте. Вывод среза элемента оформить в виде функции. Параметрами этой функции должны быть номер элемента, срез которого выводится и матрица среза. Например, объявление функции, выводящей верхний срез 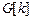k-го элемента имеет вид

void out_v_srez (int k, matrix& G);

Данная функция должна выводить все элементы вектора .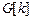

Проверка каждого свойства бинарного отношения выполняется с помощью отдельной функции, выдающей логический результат. Параметром такой функции являются матрица бинарного отношения. Например,

bool refleks(matrix& R);

Так как проверяемое свойство должно быть выполнено для всех элементов или пар элементов или троек элементов, то вначале результату функции присваивается значение true, а затем проверяется нарушение соответствующего свойства. Если условие нарушается хотя бы один раз, то функция возвращает значение false.

Контрольные вопросы

1. Что называется матрицей бинарного отношения и как она строится?

2. Дайте определение верхнего и нижнего среза элемента. Объясните способ задания бинарного отношения верхними или нижними срезами.

3. Как построить верхний и нижний срез элемента по матрице бинарного отношения?

4. Дайте определения свойств бинарного отношения и объясните алгоритмы проверки выполнения свойств по матрице бинарного отношения.