Теоретические сведения
1. Построение эйлерова цикла.
Эйлеровым циклом называется замкнутый маршрут (путь) в графе, проходящий через каждое его ребро (дугу) точно один раз.
Необходимым и достаточным условием существования эйлерова цикла в неориентированном графе является связность графа и чётность степеней всех вершин графа. Если это условие выполнено, то построить эйлеров цикл можно с помощью следующего алгоритма, который полностью повторяет доказательство достаточности теоремы. В алгоритме используются обозначения:
C – вспомогательный стек;
CE – результирующий стек, содержащий эйлеров цикл;
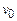 – начальная вершина цикла.
– начальная вершина цикла.
{ 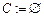 ;
; 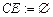 ;
; 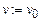 ;
; 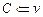 ;
;
while ( 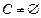 )
)
{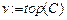 ;
;
if(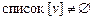 )
)
{ 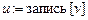 ;
; 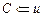 ;
;
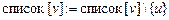 ;
;
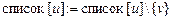 ;
;
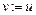 ;
;
}
else { 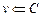 ;
; 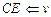 ; }
; }
}
}
Построение цикла начинается с произвольной начальной вершины, которая заносится в промежуточный стек. Далее, пока стек C не пуст, выполняется обработка его верхушки v. Если список вершины, являющейся верхушкой стека, не пуст (что означает наличие ребра, инцидентного v), то вершина списка u заносится в промежуточный стек, а ребро 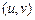 удаляется из графа. В противном случае вершина v переносится из промежуточного стека в результирующий.
удаляется из графа. В противном случае вершина v переносится из промежуточного стека в результирующий.
После окончания работы алгоритма стек CE содержит эйлеров цикл.
2. Построение гамильтонова цикла.
Так как не существует необходимого и достаточного условия гамильтоновости графа, то вопрос о существовании гамильтонова цикла решается после попытки его построения. Для построения такого цикла воспользуемся вариантом алгоритма с возвратом, который использует механизм рекурсии.
Построение цикла начинается с произвольной начальной вершины 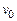 .
.
Обозначим:
x – массив, содержащий гамильтонов цикл;
Dop – массив логических переменных, означающих возможность использования вершины в цикле.
Gamilt ( k )
{ for( 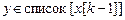 )
)
if ( ( 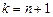 ) Ù (
) Ù ( 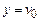 ) )вывод массива x и
) )вывод массива x и 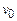 ;
;
else if ( 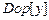 )
)
{ 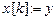 ;
; 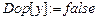 ;
;
Gamilt ( k +1);
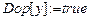 ;
;
}
}
{for( 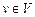 )
) 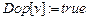 ;
;
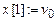 ;
; 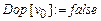 ;
;
Gamilt (2);
}
Данный алгоритм выводит все существующие гамильтоновы циклы графа.
Дата добавления: 2017-02-20; просмотров: 292;
