Пример выполнения работы.
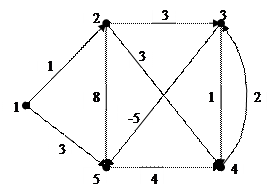 1. Рассмотрим ориентированный граф, заданный следующим входным файлом. Построим графическое представление графа, определяемого этим файлом.
1. Рассмотрим ориентированный граф, заданный следующим входным файлом. Построим графическое представление графа, определяемого этим файлом.
1 2 1
1 5 3
2 3 3
2 4 3
2 5 8
3 4 1
3 5 -5
4 3 2
5 4 4
Матрица весов дуг данного графа имеет вид
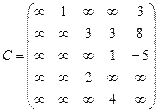 .
.
Пусть 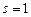 . Вычислим минимальные расстояния от вершины s до всех вершин графа. Выполним один шаг алгоритма Форда-Беллмана подробно, затем результаты работы алгоритма представим в виде таблицы.
. Вычислим минимальные расстояния от вершины s до всех вершин графа. Выполним один шаг алгоритма Форда-Беллмана подробно, затем результаты работы алгоритма представим в виде таблицы.
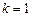
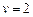
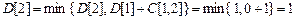
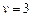
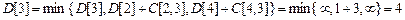
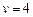
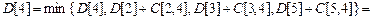

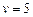
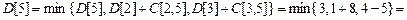
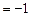
| Номер шага k | D | ||||
| ¥ | ¥ | ||||
| -1 | |||||
| -1 | |||||
| -1 |
Восстановим кратчайший путь от s до вершины 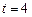 .
.
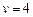 ,
,  , так как
, так как 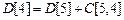
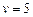 ,
, 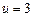 , так как
, так как 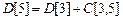
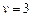 ,
, 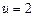 , так как
, так как 
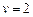 ,
, 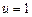 , так как
, так как 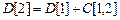
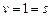 . В результате СТЕК имеет вид
. В результате СТЕК имеет вид
Следовательно, кратчайший путь между вершинами 1 и 4, длина которого равна 3: 1 ® 2 ® 3 ® 5 ® 4.
2. Рассмотрим неориентированный граф, заданный следующим входным файлом. Построим графическое представление графа, определяемого этим файлом.
 |
1 2 3
1 3 1
1 4 7
2 3 3
2 6 6
3 4 4
3 6 5
4 5 7
5 6 2
5 7 10
6 7 8
Перед построением остова 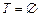 , разбиение содержит 7 компонент, каждая компонента связности содержит одну вершину, т.е.
, разбиение содержит 7 компонент, каждая компонента связности содержит одну вершину, т.е. 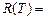
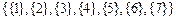 .
.
Упорядочим рёбра в порядке возрастания весов. Результат работы алгоритма Краскала оформим в виде таблицы. Обозначим через:
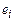 – ребро графа;
– ребро графа;
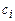 – вес ребра
– вес ребра 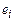 ;
;
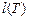 – вес остова.
– вес остова.
Если ребро графа добавляется в остов (его инцидентные вершины принадлежат разным связным компонентам остова), то 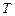 и
и 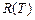 изменятся, а, следовательно, в таблицу записываем изменённые разбиение и вес остова. В противном случае соответствующие ячейки таблицы остаются пустыми.
изменятся, а, следовательно, в таблицу записываем изменённые разбиение и вес остова. В противном случае соответствующие ячейки таблицы остаются пустыми.
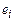
| 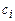
| 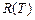
| 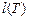
|
| (1, 3) | 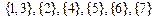
| ||
| (5, 6) | 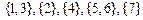
| ||
| (1, 2) | 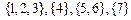
| ||
| (2, 3) | |||
| (3, 4) | 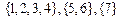
| ||
| (3, 6) | 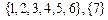
| ||
| (2, 6) | |||
| (1, 4) | |||
| (4, 5) | |||
| (6, 7) | 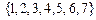
| ||
| (5, 7) |
Таким образом кратчайший остов графа суммарного веса 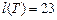 имеет вид
имеет вид
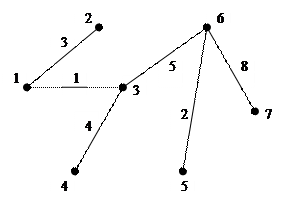 |
Контрольные вопросы
1. Каким образом находится кратчайший путь между двумя фиксированными вершинами?
2. Объясните основную идею алгоритма Форда-Беллмана.
3. Как определяется кратчайшее расстояние до вершины на каждой итерации?
4. Как восстанавливается кратчайший путь по найденным кратчайшим расстояниям?
5. Что называется кратчайшим остовом?
6. Объясните основную идею алгоритма Краскала.
Дата добавления: 2017-02-20; просмотров: 342;
