Пример выполнения работы.

1. Рассмотрим неориентированный граф, заданный следующим входным файлом. Построим графическое представление графа, определяемого этим файлом.

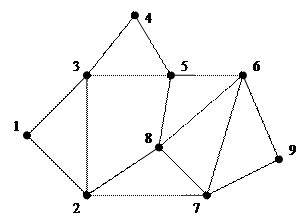1 2

1 3

2 3

2 7

2 8

3 4

3 5

4 5

5 6

5 8

6 8

6 7

6 9

7 8

7 9

Так как степени всех вершин графа чётны и граф является связным, то в нём существует эйлеров цикл. Построим его, выбрав начальной вершину 1 и считая записи в списках инцидентности вершин упорядоченными по возрастанию номеров вершин. Построим в соответствии с алгоритмом стеки C и CE. Серым цветом в стеке С выделены вершины, которые были перенесены из стека C в стек CE. Белым цветом с стеке С отмечены вершины, находящиеся с стеке на момент окончания его заполнения. Так как списки всех вершин на этом этапе пусты, то далее все они переносятся в стек CE по механизму стека (в обратном порядке).

C CE

Таким образом, эйлеров цикл имеет вид:

1 ® 2 ® 3 ® 4 ® 5 ® 6 ® 7 ® 2 ® 8 ® 6 ® 9 ® 7 ® 8 ® 5 ®

3 ® 1.

2. Определим, является ли граф из задания 1 гамильтоновым. Для этого воспользуемся алгоритмом с возвратом, работу алгоритма проиллюстрируем построением дерева решений. Вершинами данного дерева являются вершины графа, ветвями – просматриваемые варианты пути. Дерево будем заполнять в порядке просмотра вершин алгоритмом, варианты пути заполнять слева направо, т.е. ранее присмотренные варианты путей располагаются левее. Построение дерева закончим, найдя 1 вариант гамильтонова цикла или исчерпав все варианты.

Следовательно, граф является гамильтоновым, а гамильтонов цикл имеет вид: 1 ® 2 ® 7 ® 9 ® 6 ® 8 ® 5 ® 4 ® 3 ® 1.