Технология выполнения работы.

Списки инцидентности графа в языке C++ могут быть реализованы вектором, размерность которого равна количеству вершин графа. Каждый его элемент является списком, содержащим номера вершин, смежных с данной. Предварительно определения контейнерных классов vector и list должны быть подключены к файлу.

Если определить вектор, составленный из списков целых элементов, как тип graf, т.е.

typedef vector <list <int>> graf ;

то исходный граф G будет описан graf G;. Такой конструктор создаст пустой вектор.

Если граф взвешенный, то элементами его списков являются записи, содержащие помимо номера смежной вершины веса ребра (дуги), инцидентного этой вершиной.

Ввод графа осуществляется из текстового файла одного из двух видов: «таблица смежности» или «таблица ребер». Такие файлы по-разному формируются и интерпретируются для неориентированных и ориентированных графов: для неориентированного графа задаются ребра графа, а для ориентированного – дуги. То есть, ребро неориентированного графа задается один раз, а соответствующие ему записи автоматически включаются в списки инцидентности обоих его концов.

Файл «таблица смежности» состоит из блоков, соответствующих вершинам графа. Каждый блок имеет следующую структуру:

начальная вершина : список смежных с ней вершин

соответствующие ребрам (дугам) веса

Количество строк с весами ребер равно числу весов, а числ0 весов в каждой такой строке равно числу вершин в первой строке блока. Блоки в таком файле могут располагаться в произвольном порядке, причем, если вершина не является начальной ни для одного ребра (дуги) или ребро уже включено в список инцидентности другого его конца, то соответствующий ей блок отсутствует в файле.

Например, для неориентированного графа

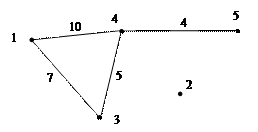
Рис. 2

файл «таблица смежности» имеет вид

1 : 3 4

7 10

3 : 4

4 : 5

а ориентированный граф

Рис. 3

задается «таблицей смежности»

1 : 2 3

2 : 3

3 : 1

Для ориентированных графов могут формироваться как списки вершин, следующих за текущей, так и предшествующих ей вершин.

Файл «таблица ребер» имеет следующую структуру:

начальная вершина конечная вершина вес(а) ребра (дуги)

Также как и для «таблицы смежности» количество элементов в каждой из строк должно быть одинаковым.

Например, файл «таблица ребер» графа, изображенного на рис.2 имеет вид.

1 3 5

1 4 10

3 4 7

4 5 4

Для формирования машинного представления графа необходимо построить список инцидентности для каждой вершины графа. Формирование списка инцидентности может осуществляться по принципу стека (LIFO), когда новая запись включается в начало списка, или по принципу очереди (FIFO), когда новая запись ставится в конец списка.

Определение количества вершин и рёбер (дуг) исходного графа лучше выполнять программно при просмотре текстового файла, здесь же можно проверять правильность заполнения файла. Количество вершин определяется как максимальный номер вершины, записанной в файл. Число рёбер (дуг) подсчитывается как суммарное число вершин для всех списков в исходном файле – для «таблицы смежности» и число строк – для «таблицы рёбер». Проверку текстового файла с одновременным подсчетом количества вершин и ребер (дуг) можно оформить функцией, которая возвращает количество вершин графа, если проверка успешна, и 0 в противном случае.

Если ошибок в файле не обнаружено, то при повторном просмотре файла выполняется формирование списков инцидентности графа. Для этого вначале создаётся нуль-граф на n вершинах с помощью метода G.resize(n). Если граф до этого не создавался пустым конструктором, тогда то же самое можно выполнить с помощью конструктора с инициализацией graf G(n);. В обоих случаях будет создан вектор, состоящий из n пустых списков.

Приведём алгоритмы построения списков инцидентности графа по входным файлам обоих видов. Используемые в алгоритмах обозначения:

nv – начальная вершина ребра (дуги);

kv – конечная вершина ребра (дуги).

1. Файл «таблица смежности».

while( не конец файла )

{ввод nv;

while ( не конец строки )

{ ввод kv;

добавить запись kv в список nv;

добавить запись nv в список kv; (для не-

ориентированного графа)

}

}

2. Файл «таблица ребер».

while( не конец файла )

{ ввод nv, kv;

добавить запись kv в список nv;

добавить запись nv в список kv; (для неориентированно-

го графа)

}

Найденные значения количества вершин и количества ребер (дуг), а также построенные списки инцидентности выводятся на экран (или выходной файл). Вывод списков инцидентности графа на экран или в файл осуществляется в соответствии со структурой аналогичной файлу «таблица смежности». При этом просматривается список каждой вершины, если он не пуст, то выводится: СП, затем в скобках вершина, : , список вершин смежных с ней. Например, выводимая информация имеет вид:

для графа (рис. 2)

СП[1]: 3 4

СП[3]: 1 4

СП[4]: 1 3 5

СП[5]: 4

для графа (рис. 3)

СП[1]: 2 3

СП[2]: 3

СП[3]: 1

Для вывода списка инцидентности или любого другого вида его обработки необходимо просмотреть этот список. Просмотр списка выполняется с помощью итераторов, которые являются аналогами указателей для контейнерных классов. Для этого итератору текущего элемента списка присваивается значение начала списка, а также запоминается итератор конца списка. Пока не достигнут конец списка, выполняются действия по обработке элемента списка и увеличение итератора текущего элемента списка. Обращение к элементу, адресуемому итератором, выполняется так же, как и для указателей, операторами * или ->.

Например, фрагмент программы просмотра и обработки i-го списка графа имеет вид:

list <int> :: iterator pl = G[i].begin(), el = G[i].end();

while (pl!=el) блок обработки элемента;

Так как граф представляет собой массив списков, то для того чтобы вывести его на печать, нужно организовать цикл печати всех списков этого массива.

При работе с графом часто требуется выполнить действия, изменяющие его структуру. К ним относятся:

1. Добавление ребра (дуги) (v_i, v_j) в граф G.

Для этого нужно:

а) добавить запись с вершиной v_j в список инцидентности вершины v_i;

б) для неориентированного графа добавить запись с вершиной v_i в список инцидентности вершины v_j.

2. Удаление ребра (дуги) (v_i, v_j) из графа G (осуществляется аналогично добавлению ребра (дуги)).

3. Удаление вершины v_i из графа G.

Для этого нужно удалить все ребра (дуги) инцидентные вершине v_i (т.е. удалить все записи из списка вершины v_i, а для неориентированных графов – и соответствующие записи из списков смежных с ней вершин).

Часто кроме изменения структуры графа для более эффективной работы алгоритмов требуется сортировка (упорядочение) списков инцидентности.

Выполнить сортировку вершин в списке (для графа без весов) и поиск вершины в списке для удаления ребра (дуги), а следовательно, и вершины, в языке С++ можно, пользуясь абстрактными алгоритмами контейнерных классов. Для этого нужно подключить к файлу определение класса алгоритмов algorithm. Если элементами списков являются записи, то сортировка вершин выполняется одним из алгоритмов сортировки.

Контрольные вопросы

1. Дайте сравнительную характеристику аналитических способов представления графа.

2. Как могут быть представлены списки инцидентности средствами языка C++?

3. Как формируются текстовые файлы, содержащие задание исходного графа?

4. Что такое итератор? Как осуществить вывод на печать построенные списки инцидентности?