Теоретические сведения

1. Построение кратчайшего пути между двумя вершинами.

Для построения такого пути нужно вначале определить кратчайшие расстояния от фиксированной начальной вершины до всех вершин графа, а затем восстановить кратчайший путь от этой вершины до заданной конечной вершины.

Для определения кратчайших расстояний от фиксированной начальной вершины до всех вершин ориентированного графа воспользуемся алгоритмом Форда-Беллмана. Обозначим через C – матрицу весов дуг графа (вес несуществующей дуги в задачах поиска минимума расстояний считаем равным +¥), D – массив кратчайших расстояний от начальной вершины s до всех вершин графа (полагаем ).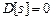

{for( ) ; ;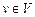

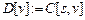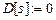for( )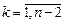

for( )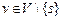

for( )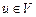

}

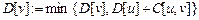
Для произвольного ориентированного графа, не содержащего циклы отрицательного веса, такие кратчайшие расстояния можно вычислить максимум за 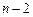итерации. На k-ой итерации алгоритма для каждой из вершин графа, кроме начальной, выполняется пересчёт кратчайших расстояний до неё от начальной вершины. Для этого определяется минимум из текущего значения расстояния до вершины и длин путей через другие вершины графа.

Количество итераций вычисления массива D можно уменьшить, сравнивая массивы в конце текущей и предыдущей

итерации (аналогично, алгоритмам сортировки). Если значения массива D не изменились на данной итерации, то вычисления заканчиваются.

Алгоритм восстановления кратчайшего пути от начальной вершины s до конечной вершины t использует механизм стека. В нём применяются следующие обозначения:

1) СТЕК 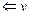– поместить вершину v в стек;

2) СТЕК – извлечь вершину v из стека.

{ СТЕК:=Æ; СТЕК ; ;

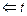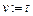while ( )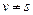

{for( )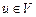

if ( 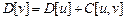)СТЕК ;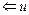

;

}

}

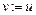Конечная вершина пути заносится в стек, и пока верхушка стека v не совпадёт с начальной вершиной s, будет определяться предыдущая вершина пути u, т.е. вершина, на которой достигается минимум.

2. Построение кратчайшего остова.

Напомним, что остовом называется остовный подграф, который является деревом. Остов, суммарный вес которого минимален, называется кратчайшим остовом.

Для построения кратчайшего остова воспользуемся алгоритмом Краскала. Обозначим через 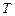– строящийся кратчайший остов, разбиение множества вершин остова на классы эквивалентности по отношению связанности вершин – .

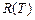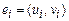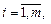
Предварительно рёбра упорядочиваются в порядке возрастания весов. Обозначим , 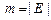. Вначале 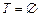, разбиение содержит n компонент связности, каждая компонента связности содержит одну вершину, т.е.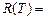 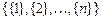. Программно разбиение 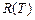можно реализовать как вектор, состоящий из множеств.

{ T:= Æ; ;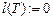

for ( i = );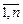

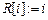for( j = )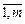

{ ; ;

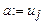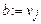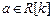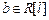if( ( ) Ù ( ) Ù ( ) )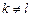

{; ;

;

}

}

}

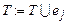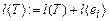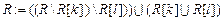Для построения остова просматриваются все рёбра графа. Если вершины, инцидентные данному ребру, принадлежат разным компонентам связности остова (т.е. вершины принадлежат разным множествам разбиения), то ребро добавляется в остов, а его вес суммируется с весом остова. Добавление ребра в остов влечёт за собой пересчёт разбиения его множества вершин, при этом два множества разбиения объединяются. В противном случае, добавления ребра не происходит, так как это повлечёт за собой появление цикла в графе.