Алгоритмы. Предварительные сведения

При анализе алгоритма решения какой-либо задачи: нас в первую очередь будет интересовать его трудоем­кость, под которой мы понимаем время выполнения соот­ветствующей программы на ЭВМ. Ясно, что этот показа­тель существенно зависит от типа используемой ЭВМ.

Чтобы сделать наши выводы о трудоемкости алгорит­мов в достаточной мере универсальными, будем считать, что все вычисления производятся на некой абстрактной вычислительной машине. Такая машина в состоянии вы­полнять арифметические операции, сравнения, пересыл­ки и операции условной и безусловной передачи управления. Эти операции считаются элементарными. Каждая из элементарных операций выполняется за единицу вре­мени и, следовательно, время работы алгоритма равно числу выполненных им элементарных операций.

Память абстрактной вычислительной машины состо­ит из неограниченного числа ячеек, имеющих адреса 1, 2, 3, ..., п, ... Ко всем ячейкам есть прямой доступ.

Остановимся особо на представлении чисел в памяти машины. При анализе алгоритмов наибольший интерес представляет зависимость времени работы алгоритма от числа вершин и (или) ребер графа. Выяснение этой за­висимости удобнее проводить, если отвлечься от величи­ны таких числовых параметров, как веса ребер взвешенного графа. Поэтому будем считать, что любое число, не­зависимо от его величины, можно разместить в одной ячейке и каждая ячейка может содержать только одно число. Сделанное допущение будет оставаться в силе на протяжении этого и следующих пяти параграфов, в кото­рых анализируется трудоемкость конкретных алгорит­мов. В последнем параграфе этой главы мы несколько изменим модель вычислительной машины, приняв, в част­ности, иной способ представления чисел.

Алгоритмы можно описывать в терминах элементар­ных операций. Однако такая запись была бы перегруже­на непринципиальными деталями, заслоняющими основ­ные идеи алгоритма.

Поэтому записывать алгоритмы будем в виде последо­вательности пунктов. Каждый пункт содержит один или несколько операторов (инструкций, правил), которые сле­дует выполнить. Внутри пункта эти инструкции выпол­няются последовательно в том порядке, как они записа­ны. Если некоторый пункт не содержит указаний на переход к другому пункту, то после выполнения всех его инструкций следует перейти к следующему по порядку пункту. Единственное требование, предъявляемое к ин­струкциям, состоит в том, чтобы каждая из них легко выражалась через элементарные операции.

В записи алгоритма некоторые его фрагменты будут сопровождаться комментариями. Комментируемый фраг­мент может быть отдельным оператором или пунктом, а также группой последовательно расположенных операто­ров либо пунктов. Комментарии будем писать в квадрат­ных скобках и помещать в начале или в конце коммен­тируемого фрагмента.

Хотя мы и условились при описании алгоритмов не ограничивать себя каким-либо набором стандартных опе­раторов, все же два таких оператора будут использовать­ся постоянно. Во-первых — это оператор присваивания а: = В. В результате его выполнения переменная а полу­чает новое значение, равное В. Во-вторых — оператор-«конец», выполнение которого означает прекращение вы­числений.

Рассмотрим теперь представление информации в па­мяти машины. Всякую конечную последовательность эле­ментов произвольной природы будем называть списком_г а число элементов списка — его длиной. Элементами мо­гут быть числа, буквы алфавита, векторы, матрицы и-т. п. В той ситуации, когда каждый элемент списка S по­мещается в одной ячейке (например, является числом),этот список будем размещать в п последовательных ячей­ках памяти, где п — длина списка. Через S(k) будем обозначать k-й элемент списка S. Аналогично список S длины п будем размещать в nd последовательных ячей­ках, если для размещения каждого его элемента доста­точно d ячеек. Такое представление списка обычно назы­вается последовательным, и ниже используется только-это представление.

Пусть А = \\A_ij\\ — матрица порядка п и А` = (A₁₁, A₁₂, ..., A_1n, A₂₁, A₂₂, ..., A_2n, ..., A_n1, A_n2 ,..., А_пп)—список ее элементов «по строкам». Принятый нами принцип «одно число — одна ячейка» означает, что матрица порядка п занимает п² ячеек памяти.

Рассмотрим теперь представление графа G в памяти машины. Пусть VG = (v₁, v₂, ..., v_n). Будем пользовать­ся тремя способами представления.

Первый — задание графа матрицей смежности. Если граф G взвешенный и w(x, у) обозначает вес ребра ху, то вместо матрицы смежности используется матрица весов W(G)=W. У этой матрицы W_jj= w(v_i v_j), если v_iv_j € EG. Если же v_iv_j ¢ EG, то полагаем W_ij = 0 или W_ij = ∞ в зависимости от задачи, которую предстоит решить. Из сказанного выше о представлении матрицы в машине следует, что такой способ задания графа требует \G\²ячеек памяти. В предыдущих главах веса предполагались неотрицательными. Теперь снимем это ограничение и бу­дем считать, что весами ребер могут быть любые вещест­венные числа.

Второй способ — задание графа списком ребер E = (е₁, е₂, ..., е_т), где т = \EG\, e_i € EG. Поскольку реб­ро графа можно хранить, используя две ячейки (по одной на каждую концевую вершину), то для хранения все­го списка E достаточно 2т ячеек. Если граф взвешенный, то под каждый элемент списка Е можно отвести три ячейки — две для ребра и одну для его веса, т. е. всего потребуется Зт ячеек.

И, наконец, последний способ, который будет исполь­зоваться,— представление графа списками смежности. При таком способе каждой вершине v_i ставится в соот­ветствие список N_vi вершин, смежных с v_i. Под этот спи­сок достаточно отвести deg v_i + 1 ячеек — по одной на каждый элемент и одну ячейку для обозначения конца списка. Кроме того, формируется список N = (N₁, N₂, ..., N_n), где N_i — номер ячейки, в которой хранится пер­вый элемент списка N_vi. Следовательно, такой способ представления графа требует ∑(deg v + 1) + п =

v € vg

= 2m + 2п ячеек памяти. Если граф G взвешенный, то для каждой вершины v_i, списка N_vi отводится дополни­тельно одна ячейка, содержащая число w(v_i ,v_j).

Хотя представление графа списком ребер является наиболее экономным «по памяти», оно имеет существен­ный недостаток. Чтобы определить, содержит ли граф данное ребро, надо просматривать поочередно элементы этого списка, а это может потребовать около 2т элемен­тарных операций. Если же граф задан списками смежно­сти, вычислительные затраты составят не более п +• 1 та­ких операций. Представление графа матрицей смежности, требующее наибольших затрат памяти, обеспечивает, как принято говорить, «прямой доступ» к ребрам графа. Уз­нать, содержит ли граф ребро v_iv_j можно, вычислив адрес k= in+j и сравнив М (k) с нулем, где М — мас­сив, в котором построчно размещена матрица смежности графа. Сказанное с очевидными изменениями переносит­ся на случай взвешенных и ориентированных графов.

Выбор того или иного задания графа зависит от кон­кретной задачи, которую предстоит решать.

Во всех рассматриваемых в этой главе задачах глав­ной частью исходной информации служит граф. Кроме этого, исходные данные могут включить номера одной или нескольких выделенных вершин. Если, например, за­дача состоит в отыскании цепи, соединяющей две задан­ные вершины графа, то помимо графа необходимо задать ломера этих двух вершин.

После того как всем исходным данным задачи присвоены конкретныезначения и они размещены в памяти ЭВМ, будем называть их входом задачи. Размером (или длиною) входа считается число ячеек, занятых входом. При анализе алгоритма решения любой задачи нас в первую очередь будет интересовать зависимость времени его работы от размера задачи, т. е. от размера входа. Од­нако, как правило, это время зависит не только от размера входа, но и от других параметров задачи, т. е. время работы алгоритма на входах одинаковой длины может быть не одинаковым. Поясним сказанное на простейшем примере. Пусть элементами списка S = (s₁, s₂, ..., s_m) яв­ляются натуральные числа и требуется определить, со­держит ли S число, кратное трем. Очевидный алгоритм решения этой простой задачи состоит в следующем: про­веряем поочередно делимость элементов списка S на 3 до тех пор, пока не встретится число s_p, кратное трем, или же не будут проверены все элементы S. Время вы­полнения р таких проверок равно t = 2p (p делений и р изменений адреса). Следовательно, при неизменной дли­не входа т время работы алгоритма будет изменяться в пределах 2 ≤ t ≤ 2т в зависимости от расположения под­ходящего элемента s_p в списке S. Наихудшим, очевидно, будет случай, когда S не содержит чисел, кратных трем, либо когда s_m — единственное такое число. Один из ос­новных подходов к определению понятия «трудоемкость алгоритма» ориентируется именно на такого рода наи­худший случай.

Определим трудоемкость (или сложность) алгоритма решения данной задачи как функцию f, ставящую в соот­ветствие каждому натуральному числу п время работы f(n) алгоритма в худшем случае на входах длины п. Ина­че говоря, f(n)—максимальное время работы алгоритма по всем входам данной задачи длины п. Анализ эффек­тивности каждого из представленных в последующих па­раграфах алгоритмов заключается в выяснении вопроса: как быстро растет функция f(n) с ростом п? При ответе на этот вопрос обычно используют O-символику.

Будем говорить, что неотрицательная функция f(n) не превосходит по порядку функцию g(n), если сущест­вует такая константа с, что f(n)< cg(n) для всех п ≥ 0; при этом будем писать f(n) = O(g(n)). Часто встречаю­щемуся далее выражению «трудоемкость (сложность) алгоритма есть (равна, составляет) O(g(n))» придается именно этот смысл. В частности, трудоемкость 0(1) означает, что время работы соответствующего алгоритма не зависит от длины входа. Иногда вместо «трудоем­кость алгоритма есть O(g(n))» будем говорить «алгоритм решает задачу за время O(g(n))».

Алгоритм с трудоемкостью О (п), где п — длина входа, называют линейным. Линейный алгоритм ограниченное (константой) число раз просматривает входную информа­цию и для подавляющего большинства «естественных» задач является неулучшаемым (по порядку) в смысле трудоемкости. Поэтому отыскание линейного алгоритма для некоторой задачи часто является своего рода «послед­ней» точкой» в ее алгоритмическом решении.

Алгоритм, сложность которого равна О(п^с), где с — константа, называется полиномиальным. Особая роль полиномиальных алгоритмов выяснится в § 78. Здесь заме­тим, что все задачи, считающиеся трудными для алгорит­мического решения, не имеют в настоящее время полино­миальных алгоритмов. Более того, понятие «полиномиаль­ный алгоритм» является сейчас наиболее распространен­ной формализацией интуитивного представления об эф­фективном алгоритме. Эта формализация, как и любая другая, не свободна от недостатков. Так, например, едва ли кто решится назвать эффективным алгоритм, время работы которого на входе длины п составляет n¹⁰⁰. Тем не менее отмеченный недостаток не столь серьезен, как это может показаться на первый взгляд. На практике дело обстоит таким образом, что появление полиномиального алгоритма решения какой-либо задачи приводит в конце концов к алгоритму, трудоемкость которого оценивается сверху полиномом небольшой степени. В большинстве случаев эта степень не превосходит трех и оценка, как правило, имеет один из следующих видов: О(п³), О(п²), О(п√n), O(nlogn), О(п).

Представленные в последующих параграфах алгорит­мы используют две важные структуры данных. Это — списки, в которых удаление элементов и включение но­вых элементов производится специальным образом.

Список S назовем стеком, если удаление и добавление элементов производится с одного конца. Выполнение этих операций осуществляется с помощью переменной t — адреса (указателя) первой ячейки, занятой последним элементом списка S. Если каждый элемент занимает d ячеек, то для удаления элемента из стека достаточно «передвинуть указатель», т. е. выполнить одну элемен­тарную операцию t := t — d. Включение какого-либо эле­мента а в стек S — это выполнение двух элементарных операций: t:— t + d, S(t):=a. Стек S пуст, если t<l, где l — адрес первой ячейки S.

Пусть, например, каждый элемент стека S = (s₁, s₂, s₃ , s₄ , s₅) занимает одну ячейку. Рассмотрим последователь­ность операций (*, *, s₇, s₈, *, s₉), где «*» означает уда­ление элемента из S, a «s_i»—добавление элемента s_i к S. Тогда S изменяется следующим образом: (s₁, s₂, s₃ , s₄), t = 4; (s₁, s₂, s₃ ), t = 3; (s₁, s₂, s₃ , s₇), t = 4; (s₁, s₂, s₃ , s₇, s₈), t = 5; (s₁, s₂, s₃ , s₇), t = 4; (s₁, s₂, s₃ , s₇, s₉), t = 5.

Список Q называется очередью, если все удаления элементов из этого списка производятся с одного конца Q, а добавления — с другого. Эти операции выполняются с помощью двух указателей l и t. Переменная t имеет тот же смысл, что и в предыдущем случае, а переменная l — это адрес первой ячейки очереди Q. Удаление элемента заключается в выполнении операции l:=l + d, а добав­ление производится точно так же, как и в случае стека. Пусть, например, Q=(q₁ , q₂ , q₃, q₄, q₅) и последователь­ность производимых над Q операций имеет вид (*, q₆ , *, * , q₇, *). Тогда результаты выполнения этих операций выглядят так: (q₂ , q₃, q₄, q₅), l = 2, t = 5; ( q₂ , q₃, q₄, q₅, q₆ ) l = 2, t = 6; (q₃, q₄, q₅, q₆), l = 3, t = 6; (q₄, q₅, q₆), l = 4, t =6; (q₄ , q₅ , q₆,, q₇), l = 4, t = 7; (q₅ , q₆ , q₇), l = 5, t = 7.

Описывая алгоритмы, мы, как правило, не указываем в явном виде механизм изменения стека или очереди. Вместо этого просто пишем «занести х в стек S (в оче­редь Q или «исключить х из стека S (из очереди Q)». Очевидно, что каждая из перечисленных операций вы­полняется за время O(1).

Будем считать, наконец, что вершины графа G, к ко­торому применяется алгоритм, занумерованы числами 1, 2, ..., |G|. Это — имена вершин, и в процессе работы алгоритма они не меняются, хотя при этом вершинам мо­гут присваиваться и другие, дополнительные номера (метки).

Поиск в глубину

В этом параграфе рассматривается один из методов обхода всех вершин и ребер графа. Этот метод, именуемый поиском в глубину (сокращенно ПГ), послужил основой для разработки ряда быстрых алгоритмов на графах. Один из таких алгоритмов — алгоритм выделения двусвязных компонент графа — приводится в § 74. Дадим вначале некоторые определения. Ориентирован­ий граф D — (V, A) назовем ориентированным деревом корнем r € V,если каждая его вершина достижима из и основание графа D — граф D_b — является деревом. В тех случаях, когда недоразумение исключено, ориентированное дерево с корнем r будем называть просто деревом.

Пусть G — неориентированный связный граф, В про­весе поиска в глубину вершинам графа G присваиваютcя номера (ПГ-номера), а его ребра помечаются. В начале ребра не помечены, вершины не имеют ПГ-номеров. Начинаем с произвольной вершины v₀. Присваиваем ей ПГ-номер ПГ(v₀)=1 и выбираем произвольное ребро v₀w Ребро v₀w помечается как «прямое», а вершина w включает (из v₀) ПГ-номер ПГ(w)=2. После этого переводим в вершину w. Пусть в результате выполнения нескольких шагов этого процесса пришли в вершину х, и Пусть k — последний присвоенный ПГ-номер. Далее действуем в зависимости от ситуации следующим образом.

1. Имеется непомеченное ребро ху. Если у вершины уже есть ПГ-номер, то ребро ху помечаем как «обратное» продолжаем поиск непомеченного ребра, инцидентного вершине х. Если же вершина у ПГ-номера не имеет, то полагаем ПГ(y) = k + 1, ребро ху помечаем как «прямое» : переходим в вершину у. Вершина у считается получив­шей свой ПГ-номер из вершины х. На следующем шаге будем просматривать ребра, инцидентные вершине у.

2. Все ребра, инцидентные вершине х, помечены. В этом случае возвращаемся в вершину, из которой х по­лучила свой ПГ-номер.

Процесс закончится, когда все ребра будут помечены : произойдет возвращение в вершину v₀.

Описанный процесс можно реализовать так, чтобы ремя работы соответствующего алгоритма составляло (/EG/ + /G/).

Такой алгоритм (алгоритм A1) мы сейчас рассмотрим. Пусть граф G задан списками смежности, т. е. N_v — список вершин, инцидентных вершине v, и v₀ — исходная вершина, с которой начинается поиск. В процессе работы алгоритма каждая вершина графа ровно один раз включается в список Q и исключается из него. Вершина включается в этот список сразу после получения ПГ-номера, исключается, как только произойдет возвращение из этой вершины. Включение и исключение вершин производятся всегда с конца списка, т. е. Q — стек. Результат работы алгоритма — четыре списка ПГ, F, Т и В: ПГ(v)— ПГ-номер вершины v; F(v)—имявершины, из которой вершина v получила свой ПГ-номер; Т и В— соответственно списки ориентированных «прямых» и «об­ратных» ребер графа G. Эти ребра получают ориентацию в процессе работы алгоритма a1. Именно, если ребро ху помечается из вершины х как «прямое», то в Т заносит­ся дуга (х, у), а если — как «обратное», то эта дуга за­носится в В.

1 ПГ(v):=1, Q(1):= v₀, F(v_o):=0, T:=¢, B:=¢, k:=1,р:=1 [k — последний присвоенный ПГ-номер, р — указатель конца стека Q, т. е. Q(p)— имя последней вершины стека Q].

2. v := Q(p) [v — исследуемая вершина].

3. Просматривая список N_v, найти такую вершину w,что ребро vw не помечено, и перейти к п. 4. Если таких вершин нет, то перейти к п. 5.

4. Если вершина w имеет ПГ-номер, то пометить ребро vw как «обратное» и занести дугу (v, w) в список В. Пе­рейти к п. 3 и продолжить просмотр списка N_v. Иначе k:=k + 1, ПГ(w):=k, F(w):=v, ребро vw пометить как «прямое» и дугу (v, w) занести в список T, р:=р+ 1, Q(p):=w [вершина w получила ПГ-номер и занесена встек Q]. Перейти к п. 2.

5. р := р — 1 [вершина v вычеркнута из Q]. Если р = 0, то конец. Иначе перейти к п. 2.

Корректность алгоритма очевидна. Оценим его трудо­емкость. Каждое включение и исключение вершины из стека Q выполняется за время O(1). Поэтому для всей работы, связанной с изменением стека Q, достаточно вре­мени O (|G|). Каждое выполнение п. 4 требует O (1) вре­мени, и для каждой вершины v € VG этот пункт выпол­няется deg v раз. Поэтому затраты на его выполнение в

целом составят O (∑deg v) = О (|EG|). Суммарное время выполнения п. 3 также составит O(|EG|), если поза­ботиться о том, чтобы каждая вершина списка N_v просма­тривалась только один раз при всех выполнениях данно­го пункта. Этого легко добиться, если, например, ввести такую новую функцию (массив) t, что t(v)—номер пер­вой непросмотренной вершины в списке N_v. Тогда сле­дующий просмотр п. 3 следует начинать с вершины z = N_v(t(v)).

Итак, трудоемкость алгоритма A1 составляет O(|EG|+|G|). Ясно, что это время является наилучшим воз­можным по порядку, так как каждая вершина и каждое ребро графа G должны быть просмотрены хотя бы один раз.

Легко видеть, что требуемый для реализации алго­ритма A1 объем памяти также составляет O(|EG|+|G|).

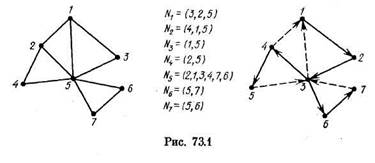
На рис. 73.1 слева изображены граф G и списки смеж­ности, которыми он задан. Справа представлены резуль­таты применения к этому графу поиска в глубину из

вершины v₀ = 1. «Прямые» ребра проведены сплошными линиями, а «обратные» пунктирными. Каждой вершине приписан ее ПГ-номер.

Из способа построения множеств Т и В непосредствен­но вытекают следующие утверждения.

Утверждение 73.1. Дуги множества Т образуют ориентированное остовное дерево с корнем в вершине v₀. Это остовное дерево часто называют остовным глубин­ным деревом (ОГД). Обозначать

его будем также че­рез Т.

Утверждение 73.2. Если ориентированное ребро (х, у) принадлежит В, то ПГ(х)>ПГ(у), т. е. «обрат­ные» ребра всегда ведут к ранее пройденным вершинам.

Поиск в глубину используется в качестве составной тасти во многих алгоритмах. Отметим одну задачу, решение которой можно получить с помощью алгоритма A1 фазу, почти без дополнительных вычислительных за­трат. Это — задача выделения связных компонент графа. Чтобы решить ее за время O(|EG|+|G|), достаточно один раз просмотреть список вершин графа, выполняя следующие действия. Если просматриваемая вершина v_l имеет ПГ-номер, то перейти к следующей. Иначе — положить v₀ = v_l ПГ(v₀) = k + 1, где k — последний присвоенный ПГ-номер, и применить поиск в глубину.Пос­ле его окончания (т. е. выделения компоненты, содержа­щей v_l) продолжить просмотр списка, перейти к верши­не v_l+1. Различать вершины разных компонент можно, например, по их ПГ-номерам, если для каждой компонен­ты запомнить последний ПГ-номер.