Наибольшие паросочетания и задача о назначениях
Задача построения наибольших паросочетаний в графе широко распространена, и для ее решения имеются эффективные алгоритмы. Эти алгоритмы основаны на методе чередующихся цепей, восходящем к Дж. Петерсену.
 |
Пусть М — паросочетание в графе G. Цепь графа G, ребра которой поочередно входят и не входят в М, называется чередующейся относительно М. Цепь длины 1
поопределению также чередующаяся. Ребра цепи называются темными или светлыми, если они входят или, соответственно, не входят вМ. Вершины графа G, инцидентные ребрам изМ, называются насыщенными, все другие вершины — ненасыщенными.
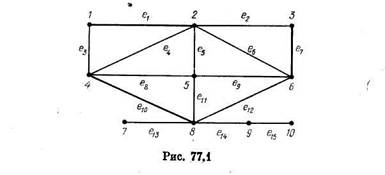
Рассмотрим, например, граф на рис. 77.1. Множество
ребер
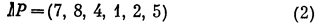 |
является в G паросочетанием;
— чередующаяся относительно М цепь; e1 = {1, 2}, e10 = {4, 8} — темные ребра Р; e3 ={1, 4}, e5 = {2, 5}, e13 ={7, 8} — светлые ребра Р; {1, 2, 3, 4, 6, 8} и {5, 7, 9, 10} — множества насыщенных и ненасыщенных вершин соответственно.
Очевидно, что если в графе G существует чередующаяся относительно паросочетания М цепь, соединяющая две несовпадающие ненасыщенные вершины, то можно построить в G паросочетание с большим числом ребер, чем в М. В самом деле, в такой цепи число темных ребер на единицу меньше числа светлых. Удалив из М все темные ребра иприсоединив все светлые, получим новоепаросочетание, вкотором число ребер на единицубольше. По этой причине чередующуюся относительно паросочетания М цепь, соединяющую две различные ненасыщенные вершины, будем называть увеличивающей относительно М цепью в графе G.
Итак, отсутствие увеличивающих относительно М цепей необходимо, если паросочетание М наибольшее. Это условие оказывается и достаточным. Именно, верна
Теорема 77.1. Паросочетание М в графе является наибольшим тогда и только тогда, когда в этом графе нет увеличивающих относительно М цепей.
Необходимость условия теоремы, как выше отмечалось, очевидна. Достаточность докажем от противного. Пусть М1 также является паросочетанием в G и| М1| > |М|. Рассмотрим граф Н, образованный ребрами, входящими в сумму М и М1 по модулю 2, т. е. в (М UMi)\ \(М П Mi). Так как произвольная вершина v этого графа инцидентна не более чем одному ребру каждого из паросочетаний М иMi, то ее степень не больше чем 2. Если deg v = 2, то одно из инцидентных вершине v ребер входит в М, другое — в М1. Поэтому любая связная компонента графа Н является либо циклом, содержащим одно и то же число ребер из М и из М1, либо чередующейся относительно М цепью. Но |М1|>|М|, следовательно, среди этих компонент обязательно есть чередующаяся относительно М цепь, крайние ребра которой (первое и последнее) входят в М1. Тогда крайние вершины этой цепи не насыщены паросочетанием М, что противоречит условию теоремы.
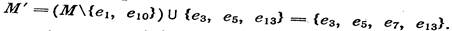 |
Для иллюстрации снова обратимся к графу G на рис. 77.1. Чередующаяся относительно паросочетания (1) цепь (2) соединяет ненасыщенные вершины 5 и 7. Следовательно, можно построить паросочетание М' с большим числом ребер:
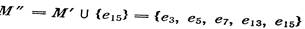 |
Паросочетание М' также не является наибольшим: (9, 10)—увеличивающая относительно М' цепь. Паросочетание
— наибольшее, α1 (G) — 5.
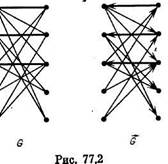 Таким образом, теорема 77.1 подсказывает следующую стратегию поиска наибольшего паросочетания: набрав с произвольного паросочетания М, строить последовательность М1 = М, М2, М3, ...., в которой паросочетание Mk+1 получается из Мк с помощью только что расcмотренного изменения вдоль некоторой увеличивающей цепи. Поскольку |Мк+1| = |Мк| +1, то для получения наиболыпего паросочетания потребуется не более |G|/2 итераций (т. е. переходов от Mh к Mh+1). В качестве М можно взять, например, произвольное ребро графа или, что лучше, некоторое максимальное паросочетание, так что исходное паросочетание всегда имеется в нашем распоряжении. Поэтому разработка эффективного алгоритма, основанного на указанной стратегии, сводится к построению процедуры, которая быстро находит увеличивающую цепь в графе, либо выявляет ее отсутствие. Ограничимся случаем двудольного графа, хотя такая процедура (а значит, и эф-зективный алгоритм отыскания наибольшего паросочета-[ия) известна и в случае произвольного графа. Итак, Пусть G = (X, У, Е) — двудольный граф и М — паросочетание в этом графе. Поставим в соответствие графу G и паросочетанию М вспомогательный ориентированный двудольный граф G =(Х, У, А), полагая А=А1 U А2 где A1 = {{y, х): x € X, y € Y, xy € M), А2={(х, у): х € = X, у € У, ху € EG\M}. Иными словами, чтобы получить граф G, достаточно придать ориентацию «от У к X» всем ребрам графа G, входящим в паросочетание М, и «от X к У» всем остальным ребрам этого графа. На рис. 77.2 изображены граф G с паросочетанием М (выделено жирными линиями) и граф G.
Таким образом, теорема 77.1 подсказывает следующую стратегию поиска наибольшего паросочетания: набрав с произвольного паросочетания М, строить последовательность М1 = М, М2, М3, ...., в которой паросочетание Mk+1 получается из Мк с помощью только что расcмотренного изменения вдоль некоторой увеличивающей цепи. Поскольку |Мк+1| = |Мк| +1, то для получения наиболыпего паросочетания потребуется не более |G|/2 итераций (т. е. переходов от Mh к Mh+1). В качестве М можно взять, например, произвольное ребро графа или, что лучше, некоторое максимальное паросочетание, так что исходное паросочетание всегда имеется в нашем распоряжении. Поэтому разработка эффективного алгоритма, основанного на указанной стратегии, сводится к построению процедуры, которая быстро находит увеличивающую цепь в графе, либо выявляет ее отсутствие. Ограничимся случаем двудольного графа, хотя такая процедура (а значит, и эф-зективный алгоритм отыскания наибольшего паросочета-[ия) известна и в случае произвольного графа. Итак, Пусть G = (X, У, Е) — двудольный граф и М — паросочетание в этом графе. Поставим в соответствие графу G и паросочетанию М вспомогательный ориентированный двудольный граф G =(Х, У, А), полагая А=А1 U А2 где A1 = {{y, х): x € X, y € Y, xy € M), А2={(х, у): х € = X, у € У, ху € EG\M}. Иными словами, чтобы получить граф G, достаточно придать ориентацию «от У к X» всем ребрам графа G, входящим в паросочетание М, и «от X к У» всем остальным ребрам этого графа. На рис. 77.2 изображены граф G с паросочетанием М (выделено жирными линиями) и граф G.
Обозначим через ХM и Ум множества ненасыщенных вершин, входящих, соответственно, в X и У. Справедливость следующего утверждения очевидна.
Утверждение 77.2. В графе G увеличивающая относительно паросочетания М цепь существует тогда и толъко тогда, когда в графе G существует (s, t)-путь, у которого s € Хм, t € Ум .
Пусть Р — (s, t)-путь в графе G, s € Хм, t € Ум, P — соответствующая увеличивающая цепь в графе G и М1 — паросочетание, полученное изменением М вдоль цепи Р. Тогда вспомогательный граф G1 для графа G и паросочетания М1 можно получить из графа G заменой каждой дуги пути Р на обратную. Эта операция вместе с поиском пути Р составляет итерацию приводимого алгоритма. Предполагается, что граф G задан списками смежности.
Алгоритм A8s построения наибольшего паросочетания в двудольном графе.
1. Построить какое-либо максимальное паросочетание М в графе G.
2. По графу G и паросочетанию М построить граф G.
3. Пусть в графе G Х- = {х: х € X, d-(x)=0}, Y+ = {у: y € Y, d+(y)=0} [в графе G X- U У+ — множество вершин, не насыщенных текущим паросочетанием]. Выполнить в графе G поиск в ширину (алгоритм A6) из множества Х-.
4. Если в результате поиска в ширину ни одна из вершин множества У+ не получила метки, то перейти к п. 5. Иначе перейти к п. 6.
5. Пусть Т={(у1 ,x1), (у2 ,x2), ...,(уk ,xk)} — множество всех дуг, выходящих из множества У. Положить М* = { у1x1, у2x2, ..., ykxk} [M* — наибольшее паросочетание]. Конец.
6. Пусть P — (s, t)-путь в графе G такой, что s € X-", t € Y+. Изменить граф G, заменив в нем каждую дугу (а, b) пути Р на дугу ( b, а). Перейти к п. 2.
Утверждение 77.3. Алгоритм A8 строит наибольшее паросочетание в двудольном графе G = (X, У, EG) за время O(|EG| min{|X|, |У|}).
To, что алгоритм корректен и построенное им паросочетание является наибольшим, следует из теоремы 77.1 и утверждения 77.2. Очевидно также, что число итераций алгоритма (т. е. выполнений п. 2—5) не превосходит величины min{|X|, |У|}, поскольку на каждой итерации, кроме последней, величины |Х-| и |У+| уменьшаются на единицу.
Согласно утверждению 76.2 п. 3 выполняется за время O(|EG|). Легко показать, что эта же оценка трудоемкости справедлива и для остальных шагов алгоритма. Таким образом, время выполнения отдельной итерации составляет O(|EG|), а алгоритма в целом — O(|EG| min{|X|, |У|}).
Вместе с наибольшим паросочетанием алгоритм A8 фактически находит и наименьшее вершинное покрытие в графе G. В результате последнего выполнения п. 3 алгоритма будет установлено отсутствие пути из Х- в У+ в графе G. Следовательно, только часть вершин этого графа будет иметь метки после окончания поиска в ширину из Х-. Обозначим через X' и У’, соответственно, множества непомеченных вершин доли X и помеченных вершин доли У. Положим Z = X' U Y'. Будем считать, что в графе G нет изолированных вершин.
Утверждение 77.4. Множество Z является наименьшим вершинным покрытием графа G.
Утверждение достаточно доказать для связных графов. Пусть (а, b)— произвольная дуга графа G. Если a € Y, b € X, то эти вершины либо обе помечены, либо нет. В обоих случаях дуга (а, b) инцидентна вершине множества Z. Пусть а € X, b € Y. Тогда, если вершина а не помечена, то a € Z. Если же а помечена, то и вершина b помечена и, следовательно, b € Z. Итак, всякая дуга графа G инцидентна некоторой вершине множества Z, т. е. Z — покрытие графа G. Кроме того, легко видеть,
что \Z\ = \Т\, где Т — множество всех дуг графа G, ведущих из множества Y. Множеству Т в графе G соответствует наибольшее паросочетание. Поэтому из теоремы 32.2 следует, что вершинное покрытие Z является наименьшим.
Использованный здесь метод чередующихся цепей играет важную роль и при решении более общих задач. Одну из них мы сейчас рассмотрим.
Пусть G — (X, Y, EG)—полный двудольный взвешенный граф, |X| = |Y|=n. Требуется найти в графе G совершенное паросочетание, вес которого минимален. Легко видеть, что это — упоминавшаяся ранее задача о назначениях (см. гл. IV, § 30).
Совершенное паросочетание минимального веса назовем для краткости оптимальным решением.
Задача о назначениях обладает двумя простыми свойствами:
1. Поскольку для каждой вершины любое совершенное паросочетание содержит в точности одно ребро, инцидентное этой вершине, то множество оптимальных решений не изменится, если веса всех ребер, инцидентных какой-либо вершине, увеличить (уменьшить) на одно и то же число.
2. Если веса всех ребер графа неотрицательны и вес некоторого совершенного паросочетания равен нулю, то оно является оптимальным решением.
Пусть, как обычно, w(x, у)—вес ребра ху. Будем считать, что w(х, у) ≥ 0 для каждого ребра ху € EG. Из первого свойства следует, что случай, когда имеются ребра отрицательного веса, сводится к нашему. Кроме того, это свойство позволяет, затратив О (п2) операций, перейти к взвешенному графу, у которого каждой вершине инцидентно ребро нулевого веса и веса всех ребер неотрицательны. Для этого достаточно изменить матрицу весов графа G. следующим образом: сначала вычесть из всех элементов каждой строки минимальный элемент этой строки, а затем то же самое проделать со столбцами. Будем считать, что эта операция уже проделана и граф G обладает требуемыми свойствами.
Пусть A € X, В € Y и α — некоторое число. Будем говорить, что к графу G применяется операция (А, В, α), если сначала из веса каждого ребра, инцидентного вершине из множества А, вычитается α, а затем к весу каждого ребра, инцидентного вершине из В, прибавляется α. Согласно свойству 1 получившийся в результате взвешенный граф имеет то же множество оптимальных решений, что и граф G. Кроме того, ребра вида аb, где а € А, b € В, в преобразованном графе будут иметь те же веса, что и в исходном. Пусть Т = (X, У, U) — двудольный граф M — паросочетание в этом графе. Будем, как и ранее, обозначать через Т = Т(Т, М) ориентированный двудольный граф, полученный из графа Т путем ориентации «от У к X» всех ребер паросочетания М и «от X к У» остальных ребер этого графа.
Будем считать, что граф G задан матрицей весов.
Алгоритм A9 построения совершенного паросочетания минимального веса в двудольном взвешенном графе.
1. Построить граф Т =(Х, У, U), U = {ху: w(x, y)=0).
2. Найти в графе Т максимальное паросочетание М.Пусть ХM ж YM — множества вершин, не насыщенных паросочетанием М и входящих, соответственно, в доли Х и Y
3. 3. Если Хм = YM = ¢ то конец [M — оптимальное решение задачи]. Иначе построить граф T = T(T, М).
4. Применить к графу Т поиск в ширину (алгоритм A6) из множества Хм. Если найден (х,y)-путь Р, х € Хм, y € YM то перейти к п. 5. Иначе перейти к п. 7.
5. Преобразовать граф Т, заменив в нем каждую дугу пути Р на обратную. Пусть Хм = (х: х € X, d-(x) = 0), YM =( y: y € Y, d+(y)=0) [путем изменения М вдоль увеличивающей цепи найдено новое паросочетание в графе Т — (Х, У, U), Хм € Х, YM € Y — подмножества вершин графа Т, не насыщенных новым паросочетанием].
6. Если Хм = YM =¢, то конец [множество всех таких ребер ху, что х € X, у € Y и (у, x)—дуга графа T, составляет совершенное паросочетание минимального веса в исходном графе G]. Иначе перейти к п. 4.
7. Пусть X' € X и Y' € Y — подмножества вершин графа Т, получивших пометки в результате поиска в ширину (в п. 4). Среди ребер графа G, имеющих вид ху, х € Х’ , y € Y — Y’, найти ребро минимального веса. Пусть α — вес этого ребра.
8. Модифицировать веса дуг графа G, применив к нему операцию (Х’, Y', α).
9. Модифицировать граф Т, добавив к нему все такие дуги (х, у), что х € Х, у €Y- Y’, w(x, y)=0, и удалив все такие дуги (х, у), что x € Х-Х’, y € Y’. Перейти к п. 4.
Займемся теперь обоснованием алгоритма A9. Корректность пп. 1—3 не вызывает сомнений. Легко видеть также, что каждый из этих пунктов можно выполнить за время О(п2). Остальные пункты алгоритма рассмотрим более подробно.
Каждое выполнение п. 5 увеличивает на единицу число вершин y € Y, для которых d+(y)= 1. Следовательно, этот пункт выполняется не более п раз. Наша ближайшая цель — показать, что после выполнения пп. 4, 6—9 не более чем п раз подряд обязательно произойдет переход к п. 5, т. е. очередное выполнение п. 4 закончится отысканием пути Р. Рассмотрим подробнее пп. 7—9. После окончания п. 4 и перехода к п. 7 каждая дуга графа Т инцидентна по крайней мере одной вершине множества (X — X') U Y. Это сразу следует из утверждения 77.4. Таким образом, каждое ребро нулевого веса в графе G инцидентно одной из вершин этого множества. С другой стороны, поскольку Хм ≠ ¢, YM ≠ ¢, то X' ≠ Х, Y' ≠ Y. Поэтому из правила выбора величины α в п. 7 следует, что α > 0. После модификации графа G в п. 8 веса всех его ребер останутся неотрицательными (это следует из правила выбора α). В результате последующей модификации графа Т (п. 9) его дуги по-прежнему будут соответствовать ребрам нулевого веса в графе G, причем дуги вида (у, х), х € X, у € Y, будут соответствовать паросочетанию нулевого веса в графе G. Модификация графа Т в п. 9 обладает двумя важными свойствами. Во-первых, удаленные дуги этого графа направлены от непомеченных вершин доли X. Поэтому все вершины, достижимые из Хм в «старом» графе Т, достижимы из этого множества и в «новом» графе Т. Во-вторых, добавленные дуги направлены от помеченных вершин доли X кнепомеченным вершинам доли Y. Таким образом, применение поиска в ширину к модифицированному графу Т (п. 4) приведет к тому, что дополнительно будет помечена по крайней мере одна вершина доли Y. Поскольку |Y| = п, то после выполнения пп. 4, 7—9 не более чем п раз подряд помеченной окажется некоторая вершина множества YM, т. е. будет найден путь Р, и затем последует выполнение п. 5. Как уже было показано, п. 5 (а значит, и п. 6) выполняется не более п раз. Поэтому каждый из пп. 4, 7—9 выполняется не более п2 раз.
Легко видеть, что трудоемкость каждого из пп. 1—9 не превосходит O(п2). Поэтому время работы алгоритма в целом оценивается сверху величиной О(п4).
Как отмечалось выше, после выполнения п. 8 веса всех ребер графа G остаются неотрицательными, и, следовательно, множество оптимальных решений не меняется. Условие окончания Хм = YM = ¢ означает, что в «последнем» графе Т имеется п дуг, направленных от X к У, которым соответствует совершенное паросочетание нулевого веса в «последнем» графе G. Согласно свойству 2 оно является оптимальным решением исходной задачи.
Резюмируем все выше изложенное в виде теоремы.
Теорема 77.5. Алгоритм Ад строит совершенное паросочетание минимального веса в двудольном взве шенном графе G=*(X, Y, EG), |X| =|Y|=n, за время О(п4).
Замечание. Известен алгоритм, решающий эту задачу за время О(п3). В алгоритме A9 оценка О(п4) возникает, по существу, из-за того, что приходится О(п2) раз выполнять операцию (X', Y', α), которая сама требует времени О(п2). Снижение оценки до О(п3) достигается за счет того, что результат этой операции удается получить за время О(п).
 |
Недавно опубликован алгоритм, оценка трудоемкости которого во многих случаях предпочтительнее 0(п3). Эта
Рис. 77.3
Оценка имеет вид О (п2-5 log (пТ)), где Т— наибольший из весов ребер графа.
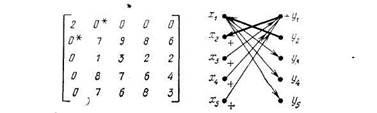
Пример. На рис. 77.3 представлена матрица весов V=|| Wij || двудольного графа G=(X, Y, EG), у которой Vij = w (xi, xj), xi € X, yj € Y. Там же изображен граф G, построенный по максимальному паросочетанию М = (x2y1, x1y2) нулевого веса в графе G. Соответствующие этому паросочетанию дуги графа Т обведены жирными линиями, а элементы матрицы W отмечены звездочками. Перед первым выполнением п. 4 имеем Хм = {х3,, х4 , х5} , YM = {y3,, y4 ,y5}. Поиск в ширину из Хм дает X' = { х2 , х3,, х4 , х5}, Y' = {y1}. Вершины множества X' U Y' будем отмечать значком «+». Поскольку пути из Xм в YM нет, то переходим к пп. 7—9. Находим α = W32 = 1 и выполняем операцию ({ х2 , х3,, х4 , х5},{y1}, 1), т. е. вычитаем 1 из всех элементов в строках 2, 3, 4, 5 и прибавляем это число ко всем элементам первого столбца. В результате к графу Т добавится дуга (х3 , y2). Модиицированная матрица W (т. е. граф G) и граф Т представлены на рис. 77.4.
Применение поиска в ширину к графу Т дает путь = (х3 , y2,, х1 , y5) из Хм в YM. Заменим (выполнение 5) в графе Т дуги (х3 , y2,), (y2 , x1), (х1 , y5)соответственно на дуги (y2 , x3), (x1 , y2), (y5 x1). Новый граф Т также изображен на рис. 77.4. В нем Хм = { х4 , х5}, YM ={y3,, y4 }.
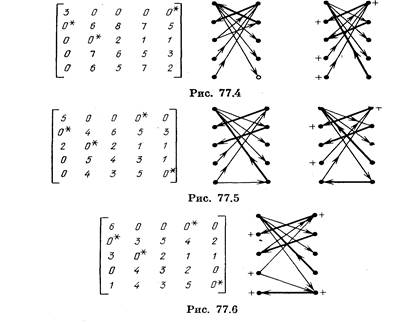 |
Снова выполнив поиск в ширину из Хм, получим X' = {х2 , х4 , х5}, Y' = {y1}. Среди элементов матрицы W, лежащих на пересечении строк с номерами 2, 4, 5 и столбцов с номерами 2, 3, 4, 5, находим минимальный.
Получим α= W55 = 2. Результаты последующего применения к графу G операции ({ х2 , х4 , х5},{y1}, 2) и модифицированный граф Т представлены на рис. 77.5. В этом графе имеется путь Р=(х5, y5 ,х1, у1) из Хм в YM.
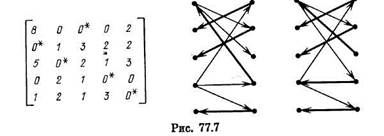 |
«Новый» граф T, полученный в результате выполнения п. 5, также изображен на рис. 77.5. Поиск в ширину в этом графе из множества Хм={х4} дает X' = {х2 , x4}, Y' = {у1}. Находим α = W45 = 1. Результаты последующего выполнения пп. 8, 9 представлены на рис. 77.6. Поиск в ширину из x4 дает X' ={ х2 , х4 , х5}, Y' = {y1 ,у5}.Находим α= W44 = 2. Получаем новые матрицу и граф Т (рис. 77.7). В графе Т имеется (х4 , у3)-путь Р = (х4 , у4, х1 , у3). Изменив этот граф в соответствии с п. 5, получим новый (рис. 77.7), в котором Хм = YM = ¢. Пять его дуг, ведущих «от X к Y», соответствуют ребрам
совершенного паросочетания минимального веса в исходном графе G. Вес этого паросочетания равен 0 + 0 + 1 + + 6 + 3 = 10.
Дата добавления: 2019-07-26; просмотров: 1329;
