Отыскание двусвязных компонент
В этом параграфе мы рассмотрим применение поиска в глубину к выделению 2-связных компонент графа. Здесь дело обстоит не так просто, как в предыдущей задаче. Конечно, можно было бы, удаляя поочередно вершины графа и каждый раз выделяя связные компоненты, найти его точки сочленения и блоки. Такой подход, однако, приводит к алгоритму сложности по крайней мере O(|EG|*|G|)Использование более глубоких свойств ПГ позволяет получить линейный по сложности алгоритм решения этой задачи.
В дальнейшем удобно использовать следующие термины. Пусть D=(V, А)—ориентированное дерево, х, у € V. Назовем х отцом вершины у, а у — сыном вершины х, если дуга (х, у) принадлежит А. Будем говорить, что вершины хиу сравнимы, если одна из них достижима из другой. Если при этом у достижима из х, то х — предок вершины у, а у — потомок вершины х. Подграф графа D, порожденный множеством, состоящим из вершины у и всех ее потомков, будем обозначать через Dv и называть поддеревом с корнем у.
Пусть в графе G проделан поиск в глубину из вершины v0 и получены остовное глубинное дерево Т и множество обратных ребер В.
Следующие три утверждения дают теоретическую основу для разработки эффективного алгоритма выделения двусвязных компонент.
Утверждение 74.1. Если дуга (х, у) принадлежит В, то х является потомком вершины у в Т.
Надо доказать, что вершина х принадлежит поддереву Ту. Предположим противное. Согласно утверждению 73.2 вершина х получает свой ПГ-номер позже, чем у. Поэтому присвоение вершине х ПГ-номера произойдет не раньше, чем будут посещены все вершины дерева Ту и произойдет возвращение в вершину s = F(y). Но возвращение в s не может произойти прежде, чем все вершины множества Ny получат ПГ-номера. Поскольку х € Ny и ПГ-номера к этому моменту не имеет, то получаем противоречие.
 |
Следующие два утверждения показывают, каким образом поиск в глубину «реагирует» на точки сочленения графа.
Утверждение 74.2. Вершина vo является точкой сочленения графа G тогда и только тогда, когда она имеет не менее двух сыновей.
Пусть v0 — точка сочленения графа G. Ясно, что каждый блок графа, включающий вершину v0, содержит по крайней мере одного из ее сыновей.
Пусть теперь s1 , s2, ..., sk — сыновья вершины v0. Рассмотрим поддеревья TSi (i = 1, k). Ясно, что VG— v0 = U VTSi. Для доказательства несвязности графа G — v0 достаточно показать, что в этом графе нет ребер, связывающих вершины различных TSi. Но это сразу следует из утверждения 74.1.
Будем говорить, что х — собственный предок (потомок) вершины у, если х — предок (потомок) у и х ≠ у.
Утверждение 74.3. Вершина v≠v0 является точкой сочленения графа G тогда и только тогда, когда для некоторого сына s этой вершины не существует дуги (х, у) € В такой, что х — потомок (не обязательно собственный) вершины s, а у — собственный предок вершины v.
Пусть v — точка сочленения графа G и G1, G2, ..., Gm, m ≥ 2,— блоки этого графа, содержащие вершину v. Пусть, далее, v' = F(v), т. е. v' — отец вершины v.Не теряя общности считаем, что вершина v' содержится в блоке G1. Каждый из остальных блоков Gi(i = 2, m)должен, очевидно, содержать хотя бы одну вершину, являющуюся сыном вершины v. Пусть, например, s — сын
вершины v и s € G2. Если теперь допустить существование «обратного» ребра ab (т. е. дуги (а, b)€ В) такого, что а — потомок s, а b — собственный предок вершины v,то придем к существованию в графе G простого цикла,содержащего вершины v' и s. Этот цикл образован простой (а,b)-цепью, состоящей из «прямых» ребер и «обратного» ребра ab. Это означает (согласно утверждению 36.3), что вершины s и v' принадлежат одному блоку. Получили противоречие.
Докажем теперь вторую часть утверждения. Пусть вершина s является сыном вершины v, для которого выполняется условие, фигурирующее в формулировке утверждения. Это условие вместе с утверждением 74.1 означает, что если ab—«обратное» ребро и а € Та, то либо b € Та, либо b = v. Последнее означает, что все ребра графа G, связывающие вершины множества VTа с вершинами VG\VTа, инцидентны вершине v, т. е. v-—точка сочленения графа G.
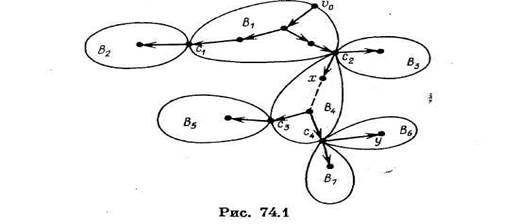
Перейдем теперь непосредственно к разработке алгоритма выделения блоков графа. Чтобы уяснить схему применения ПГ к решению этой задачи, обратимся к примеру.На рис.74.1 изображен граф «с точностью до блоков». ПГ начинается в вершине v0. После нескольких шагов придем в одну из точек сочленения графа, например, в c2. Пусть, далее, выбирается и помечается как «прямое» ребро c2x блока В4. После этого дальнейшая работа ПГ вплоть до возвращения в c2 происходит точно так, как если бы было v0 = c2 и блоков В1, В2, В3 в графе G не было бы вовсе. Поэтому возвращение в Сг из х будет означать, что пройдены все ребра блоков В4 , В5, В6.,В7 .Таким образом, возвращение в c2 произойдет позже, чем возвращения в c3 и c4 из висячих блоков В5, В6.,В7. Эти рассмотрения приводят к следующему важному выводу. Самое первое возвращение в точку сочленения произойдет сразу же после завершения обхода всех ребер некоторого висячего блока Вк. Это же справедливо и по отношению к дальнейшему поведению ПГ в графе, полученном из графа G удалением блока Bh.
Покажем, как использовать сказанное выше в предположении, что у нас есть способ, позволяющий при каждом возвращении из вершины v в F(v) определять, является ли F(v) точкой сочленения. С этой целью заведем стек S, в который будем заносить всякое ребро графа G сразу после получения им пометки «прямое» или «обратное». Таким образом, все ребра добавляются в конец списка S. Пусть в нашем примере возвращение из вершины у в c4 (см. рис. 74.1) является самым первым возвращением в точку сочленения. Тогда к моменту возвращения в c4 ребра блока В6 будут занимать все t последних мест в стеке S, где t — число ребер этого блока. Важно при этом, что ребро c4 у занимает первое среди t указанных мест. Это позволяет, просматривая стек S справа налево, выделить (т. е., например, переместить з отдельный список) все ребра блока В6. Затем эти ребра удаляются из S.
Итак, учитывая сказанное, необходимо уметь в процессе ПГ быстро определять возвращение в вершину, являющуюся точкой сочленения. Утверждения 74.2 и 74.3 дают соответствующие критерии, и нам надо их «алгоритмизировать». С этой целью для каждой вершины v € VG шределим множество P(v). В это множество включим вершину v и каждого ее предка w, для которого существует «обратное» ребро xw такое, что х — потомок вершины v в остовном глубинном дереве Т. Иными словами, множество P(v) состоит из всех предков вершины v, которых можно достичь из v, проходя сначала несколько (возможно, ни одной) дуг дерева Т, а затем одну дугу множества В.
Введем теперь функцию l(v), v € VG, полагая l(v) = min ПГ(x). Например, в графе на рис. 73.1 l(l) = 1, l(2) = 1, l(3) = l,l(4) = 3, l(5) =1, l(6)=3,l(7)=3.
Используя функцию l(v), сформулируем утверждение 74.3 в следующем виде, более удобном для организации вычислений.
Утверждение 74.4. Вершина v≠v0 является точкой сочленения графа G тогда и только тогда, когда существует такой сын s этой вершины, что l(s)≥ ПГ(v).
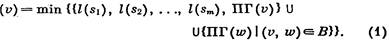 |
Вычислить значение l(v) нетрудно, если известны значения функции l для всех сыновей вершины v. Именно, если s1, s2 , ..., sm — сыновья вершины v, то имеет место формула
Справедливость этого соотношения становится очевидной, если заметить следующее. Множество предков вершины v, достижимых из нее с использованием дуг дерева Т и не более одной дуги из В, состоит из предков v, достижимых таким же способом из вершин s1, s2 , ..., sm и множества вершин, к которым ведут обратные ребра от вершины v.
Используя соотношение (1), функцию l можно вычислять попутно с выполнением обычных операций поиска в глубину. При первом посещении вершины v вместе с присвоением ПГ-номера полагаем l(v) = ПГ(v). В дальнейшем это значение корректируется в соответствии с формулой (1) следующим образом. Всякий раз, когда происходит возвращение в вершину v из некоторого ее сына s, полагаем l(v):=min{l(s), l(v)}. Кроме того, когда некоторое ребро vw помечается как «обратное», полагаем l(v):=min{l(v), ПГ(w)}. К моменту возвращения из v в вершину x=F(v) будет вычислено истинное значение l(v), которое в дальнейшем используется для корректировки l(х). Существенно, что каждая из этих корректировок требует только O(1) дополнительного времени. Поэтому ПГ вместе с вычислением функции l по-прежнему будет выполняться за время O(|EG|+|G|).
Еще одна добавка к «стандартному» поиску в глубину связана с точками сочленения. Для обнаружения точки сочленения достаточно после каждого возвращения в вершину v из некоторого ее сына s сравнить величины l(s) и ПГ(v). Если окажется, что l(s) ≥ ПГ(v), то все ребра стека S, начиная с последнего и кончая sv, удаляются из этого списка. Удаленные ребра составляют один из блоков графа G. Согласно утверждению 74.4 неравенство l(s) ≥ ПГ(v) означает, что либо вершина v — точка сочленения, либо v = v0 и v не является точкой сочленения. Заметим, что второй случай не требует особого рассмотрения. В этом случае удаленные из стека S ребра соответствуют единственному блоку графа, содержащему v0. И, наконец, последняя деталь. Выделение блока графа G мы понимаем как удаление всех ребер этого блока из стека S. Можно считать, что одновременно с удалением из S каждое такое ребро заносится в некоторый другой список, причем множество ребер разных блоков разделены в этом списке, например, символом 0. Процедура построения этого нового списка очевидна, и чтобы не загромождать описания алгоритма, мы не приводимее в явном виде.
Сравнение l(s) с ПГ(v) производится |G| — 1 раз, и, следовательно, суммарное время, затраченное на выполнение сравнений, составляет O(|G|). Каждое ребро графа один раз включается в стек S и один раз исключается из него. Поэтому вся работа, связанная с изменением S, выполняется за время O(|EG|). Таким образом, поиск в глубину вместе с выделением блоков будет выполняться за время O(|EG|+|G|).
Алгоритм A2 поиска в глубину с выделением двусвязных компонент.
1.ПГ(v0):=1, l(vo):=1, S:=¢, F(v0):=0, T:=¢, В:= ¢, k :=1,p:= 1, Q(1):= v0.
2.v:=Q(p).
3.Просматривая список Nv, найти такую вершину w,что ребро vw не помечено, и перейти к п. 4. Если таких вершин нет, то перейти к п. 5.
4. Если вершина w имеет ПГ-номер, то поместить ребро vw как «обратное», занести ребро vw в стек S, l(v): = min{l(v), ПГ(w)} [выполнена корректировка l(v)].Перейти к п. 3 и продолжить просмотр списка Nv. Иначе ребро vw пометить как «прямое», k := k + 1, ПГ(w):=k,l(w):=k, F(w):= v,p:=p + 1, Q(p):= w. Перейти к п. 2.
5. р := р — 1. Если р = 0, то конец. Иначе перейти к п. 6.
6.Пусть x = F(v). Если l(v)> ПГ(x), то перейти к п. 7. Иначе l(x):= {l(x), l(v)} [выполнена корректировка 1{х)]и перейти к п. 2.
7.Удалить из стека S все ребра вплоть до xv [удаленные ребра составляют блок графа G]. Перейти к п. 2.
Пример. На рис. 74.2 изображен граф G и приведены списки смежности его вершин. Этот граф имеет четыре блока В1 , В2 , В3 , В4 и две точки сочленения d и х. Поиск в глубину начинается с вершины α, т. е. vo=α. На рис. 74.3 отражена ситуация, сложившаяся непосредственно перед выделением блока В4. К этому моменту шесть ребер помечены как «прямые» и одно как «обратное». Прямые ребра проведены жирными линиями, а обратное — пунктирной. Тем и другим придана соответствующая ориентация. Помеченные ребра расположены в стеке S в том порядке, в котором они получали пометки. Пара чисел (α, β), приписанная вершине v, имеет следующий смысл: α = ПГ(v), a β — значение l(v), вычисленное к рассматриваемому моменту.
 |
После того, как ребро tx получило пометку «обратное», произошло возвращение в вершину z. При этом сравнение величин ПГ(z)=6 и l(t) = 5показало, что вершина z не является точкой сочленения. Далее при возвращении
из вершины z в х обнаруживается, что l(z) = 5= ПГ(x). Следовательно, все ребра от tx до xz в стеке S составляют блок графа G. Эти ребра —tx, tz, xz — удаляются из S, и тем самым выделен блок В4..
После этого алгоритм работает так, как если бы блока В4. в графе G не было вообще. Ключевые моменты
 |
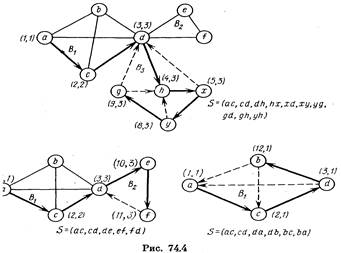 |
дальнейшей работы алгоритма иллюстрируются на рис. 74.4. Каждый из трех графов (вместе с их пометками и стеком S), изображенных на этом рисунке, отражает ситуацию, создавшуюся непосредственно перед удалением очередного блока. Выделение последнего блока, т.е. удаление его ребер из стека S, произойдет при возвращении в вершину v0 = а, для которой ПГ (а) = 1 =l(с). Таким образом, на вершину vo — a алгоритм реагирует» точно так же, как на точку сочленения.
В заключение отметим, что поиск в глубину оказывается полезным и при отыскании 3-связных компонент графа. Известен основанный на поиске в глубину алгоритм, решающий эту задачу за время O(|EG|+|G|).
Минимальный остов
Задача о минимальном остове состоит в отыскании остова минимального веса во взвешенном графе (G, w). Она считается одной из самых «легких» оптимизационных задач на графах. Решение этой задачи можно получить с помощью «жадного» алгоритма, если указать процедуру» которая по любому ациклическому множеству ребер X€ EG и ребру е €EG определяет, содержит ли множество реберX U е цикл графа G. В качестве такой процедуры можно использовать, например, поиск в глубину, поскольку выявление цикла в множестве X U е, где е = ab, равнозначно отысканию (a, b) -цепи в порожденном подграфе G(X). В процессе работы «жадного» алгоритма эта процедура выполняется не более |Е| раз, и, следовательно, затраты времени составят O(|EG|•|G|). Для упорядочения множества EG по неубыванию весов известны алгоритмы сложности O(|EG|log|G|). Таким образом, даже бесхитростная реализация «жадной» стратегии поиска минимального остова приводит (независимо от способа задания графа G) к алгоритму сложности O(|EG|•|G|), т. е. к полиномиальному алгоритму. С этой точки зрения задача о минимальном остове действительно является легкой.
Мы сейчас рассмотрим два алгоритма решения этой задачи, имеющие лучшие оценки быстродействия.
Пусть T = {( T1, V1,), (V2, T2), ...,(Vk, Tk)}-остовный лес взвешенного графа G, Vi и Тi — множества вершин и ребер i-й компоненты леса Т, w(x, у)—вес ребра ху графа G. Оба алгоритма построения минимального остова опираются на следующую простую теорему.
Теорема 75.1. Пусть ребро аb имеет минимальный вес среди всех ребер, у которых ровно один конец содержится в VT1. Тогда среди остовов графа G, содержащих Т U ab, найдется такой, вес которого не более веса любого остова, содержащего Т.
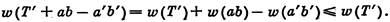 |
Пусть Т' — произвольный остов графа G, содержащий T и не содержащий ребра аb. Добавим это ребро к Т'. Полученный граф будет содержать цикл S (теорема 13.1). Этот цикл включает ребро ab и по крайней мере еще одно ребро а'b', у которого ровно один конец содержится в V1. По условию w(a, b)≤(a', b'). Следовательно,
С другой стороны, граф T’+ab — a’b' является остовом графа G, содержащим Т U ab.
Замечание. Легко показать, что каждый минимальный остов должен содержать по крайней мере одно из ребер минимального веса графа G. Следовательно, всякий алгоритм построения минимального остова должен хотя бы раз просмотреть всю входную информацию, будь то матрица весов, список ребер или списки смежности графа. В противном случае непросмотренное ребро может оказаться единственным ребром минимального ве  са графа, иэто ребро не сможет войти в минимальный остов.
са графа, иэто ребро не сможет войти в минимальный остов.
Теорема сразу подсказывает следующую стратегию построения минимального остова. На первом шаге рассмотрим остовный лес Т1 с n=|G| компонентами. Каждая его компонента состоит из одной вершины, т. е. Vi1 = {vi}. Этот лес, очевидно, содержится в любом остове графа G. Среди ребер, инцидентных vi , выберем ребро минимального веса v1vx1 и присоединим его к Т1. Согласно теореме 75.1 существует минимальный остов, содержащий лес Т2 = Т1 U {v1vx1}, у которого компонента (V12, T12) cодержит две вершины v1 и vx1 и ребро v1vx1k ,а остальные компоненты одновершинные. На следующем шаге будет выбрано и добавлено к Т2 ребро минимального веса среди ребер, соединяющих, {v1 ,vx1} с VG\{v1, vh1} и т. д.
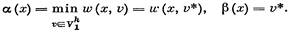 |
Итак, стратегия построения минимального остова совершенно ясна: на каждом шаге присоединяется ребро, минимальное по весу среди ребер, соединяющих уже построенный фрагмент минимального остова с вершинами, еще не включенными во фрагмент. Нам остается только позаботиться об экономной реализации шагов этого провеса. С этой целью свяжем с каждой вершиной х € VG. Две метки α(х) и β(х), смысл которых заключается в следующем. Пусть проделано k шагов и (V1k, T1k) — фрагмент минимального остова, построенный к этому моменту, т. е. это компонента леса, к которой на предыдущих этапах присоединялись ребра минимального веса. Тогда
Таким образом, α (х) — вес минимального по весу ребру, соединяющего вершину х с построенным фрагментом мимального остова, а β(х)—имя второй вершины это-ребра. Метки α(х) и β(х) позволяют быстро находить в каждом шаге ребро минимального веса. Кроме того, после присоединения очередной вершины v к фрагменту ветки легко подкорректировать. Для этого достаточно сравнить «старое» значение α(х) с w(v, x) и выбрать из них меньшее в качестве «нового» значения α(х).
В приводимом ниже описании алгоритма построения минимального остова помимо α(х) и β(х) использованы следующие обозначения: VT, ЕТ — множества вершин и ребер строящегося фрагмента минимального остова; Nx —окружение вершины х; |G| = п. Граф G задан матрицей весов.
Алгоритм A3 построения минимального остова.
1. Положить ЕТ := ¢, VT := {а}, где а — любая вершина из VG. Каждой верщине х ≠ а приписать метки α(х)= w(x, а), если x €Na, иα(x)= ∞, если x ¢ Na, β(x) = а.
2.
 |
[отыскание вершины, «ближайшей» к фрагменту].Выбрать вершину v* € VG\VT согласно условию
3. [увеличение фрагмента]. Пусть v‘= β(v *). Изменить VT и ЕТ, полагая VT := VT U {v*}, ЕТ : = ET U v'v*.
4. Если |VT| = n , то конец. Ребра, находящиеся в множестве ЕТ, составляют минимальный остов.
5. Для каждой вершины v € Nv* ∩ (VG\VT) изменить метки следующим образом. Если α(v)> w(v*, v),то α(v):= w(v*, v), β(v):= v*. Если же а(v) ≤ w(v*, v),то метку вершины v не менять. Перейти к п. 2.
Утверждение 75.2. Алгоритм A3 строит минимальный остов за время O(|G|2).
Так как всякий раз к ЕТ добавляется ребро, один конец которого принадлежит VT, а другой нет, то граф Т = (VT, ЕТ) на каждом шаге является деревом. После завершения работы алгоритма это дерево будет остовным, поскольку алгоритм прекращает работу только если VT = VG.
Докажем минимальность остова Т. Для этого достаточно доказать, что после k-го (k = 1, п— 1) выполнения п. 3 алгоритма граф Тк = (VTh, ETh) содержится в некотором минимальном остове. Доказывать будем индукцией по k. При k = 1 наше утверждение непосредственно следует из теоремы 75.1. Предположим, что оно справедливо для некоторого k > 1, т. е. граф Тк, построенный в результате k выполнений п. 3, содержится в некотором минимальном остове. Учитывая правило выбора ребра е для присоединения к Th, применим теорему 75.1. Получим, что граф Th+1 = Тк U е, построенный в результате (k + 1)-говыполнения п. 3, также содержится в некотором минимальном остове.
Выясним теперь быстродействие алгоритма. Однократное выполнение п. 2 требует времени не более O(|G|). Столько же времени достаточно для обновления меток в п. 5, а п. 3 и п. 4 выполняются за время O(1). Поскольку каждый из пп. 2—5 выполняется п — 1 раз, то оценка трудоемкости алгоритма — O(|G|2).
Пример 1. На рис. 75.1 изображены граф G и последовательность Тi (I = 1, п — 1) фрагментов минимального остова, получающихся после каждой итерации алгоритма. Числа, приписанные ребрам графа G, означают
 |
веса этих ребер. Каждой вершине х, еще не вошедшей в Тi приписана пара чисел [α(x), β(x)], которыми она помечена в результате i-го выполнения п. 5 алгоритма.
Если граф G задан матрицей весов, то всякий алгоритм построения минимального остова в таком графе будет иметь сложность не менее чем O(|G|2), поскольку он, согласно замечанию 1, должен просматривать все элементы матрицы весов. Следовательно, в этой ситуации алгоритм A3 имеет неуменьшаемую по порядку трудоемкость. Если же граф G задан списком ребер либо списками смежности и |EG| существенно меньше чем |G|2, то быстродействие алгоритма A3 далеко от оптимального. Другими словами, алгоритм A3 недостаточно эффективен в применении к «редким» графам, т. е. к графам, слабо насыщенным ребрами.
Рассмотрим еще один алгоритм построения минимального остова, ориентированный на работу именно с такими графами. Этот алгоритм (алгоритм A4), как и предыдущий, опирается на теорему 75.1, однако более полно использует предоставляемые ею возможности. Именно, если в алгоритме A3 ребро присоединяется всякий раз к одной и той же компоненте леса, то в алгоритме A4 ребра присоединяются к каждой компоненте.
Пусть T = {( V1, Т1), ..., (Vp, Tp)} — остовный лес графа G. Назовем ребро аb минимальным по весу для компоненты (Vl ,Tl),1 ≤ l ≤ p, если a € Vl ,b¢ Vl и w(a,b)=min w(x,y). Будем говорить, что М = М(Т) - множество минимальных по весу ребер для леса T, если для каждого l = 1, р множество М содержит хотя бы одно минимальное по весу ребро для компоненты (Vl ,Tl) и, кроме того, М — минимальное по включению множество, обладающее этим свойством.
Утверждение 75.3. Если М — множество минимальных по весу ребер для T={( V1, Т1), ..., (Vp, Tp)}, то граф Т' = Т + М не содержит циклов.
Доказываем от противного. Предположим, что Т содержит цикл S, который не теряя общности будем считать простым. Пусть a1b1 , a2b2 , ... , albl — ребра множества S ∩ М, выписанные в той последовательности, как они расположены в цикле S. Этой последовательности соответствует последовательность компонент (Vk1, Tk1), (Vk2 , Tk2) , ..., (Vkl , Tkl) леса Т, такая, что а1 € Vk1, b1 € Vk2, a2 € Vk2 , b2 € Vk3 , ..., аl € Vkl , bl € Vkl.. Выберем среди ребер аibi ( i = 1, l) максимальное по весу. Пусть это будет ребро а1b1 . Ясно, что а1b1 является минимальным по весу ребром по крайней мере для одной из компонент (Vkl , Tkl) или (Vk2 , Tk2). He теряя общности считаем, что ребро а1b1 — минимальное по весу для (Vk1, Tk1). Тогда w(а1 , b1)=w(аi , bi) и, следовательно, множество M \ а1b1 содержит хотя бы одно минимальное по весу ребро для каждой компоненты леса Т. Последнее противоречит минимальности множества М.
Перейдем теперь к изложению алгоритма A4.Этот алгоритм, так же, как и A3, на первой итерации имеет дело с остовным лесом графа G, состоящим из п=|G| одновершинных компонент. Каждая итерация алгоритма состоит в следующем. Вначале строится множество М минимальных по весу ребер для леса Т, полученного в результате предыдущих итераций. (Важно отметить, что сделать это можно за один просмотр элементов множества EG.). Затем с помощью поиска в глубину выделяются связные компоненты графа Т' = Т + М, который согласно утверждению 75.2 является лесом. После этого начинается следующая итерация с новым лесом Т’ имеющим, очевидно, меньше компонент, чем Т.
В приводимом ниже описании алгоритма A4 используются следующие обозначения. Ребра графа G содержатся в списке Е, т. е. E(i)—пара номеров концевых вершил i-го ребра. Список W содержит веса ребер графа G, т. е. W(i)—вес i-горебра. Чтобы каждый раз строить множество минимальных по весу ребер для текущего леса заюдин просмотр списка Е, используются списки НМР, BMP и КОМП:
НМР (i)—номер минимального по весу ребра для i-йкомпоненты текущего леса;
BMP (i)—вес этого ребра;
КОМП (j)— номер компоненты текущего леса, содержащей вершину j.
Пусть, далее, ЕТ — множество ребер текущего леса Т, а р — число его компонент; Е1 — множество минимальных по весу ребер для текущего леса Т.
Алгоритм A4 построения минимального остова.
1. ЕТ:=¢, КОМП(i):=i, ВМР(i):=∞ для i = 1,n , р:= п. [Пп. 2—8 —построение множества Е1 минимальных по весу ребер для леса Т].
2. k:=1.
3. Пусть E(k) = uv; i:=КОМП(u), j:=КОМП(v) [i и j — номера компонент леса, содержащих вершины и и v соответственно].
4. Если i≠ j, то перейти к п. 5, иначе перейти к п. 7.
5. Если w(u, v)= W(k) < BMP (j), то BMP (j): = w(u, v), HMP(j):=k.
6. Если w(u, v)=W{k)<BMP(i), то ВМР(i): =w(u, v), HMP(i):=k.
7. Если k = |EG|, то перейти к п. 8. Иначе k := k +1 и перейти к п. 3. [К моменту выполнения п. 8 первые р элементов НМР содержат номера ребер, составляющих множество минимальных по весу ребер для Т.]
8. Просмотреть первые р элементов массива НМР и сформировать множество Е1 минимальных по весу ребер для леса Т.
9.ET:=ET U Ei [ЕТ — множество ребер «нового» леса Т'].
10. Выделить с помощью алгоритма поиска в глубину связные компоненты графа Т' = Т + E1 [обновлен список КОМП,получено новое значение р].
11. Если р = 1, то конец [ЕТ — множество ребер минимального остова]. Иначе перейти к п. 2.
Утверждение 75.4. Алгоритм A4 строит минимальный остов за время O(|EG| log |G|).
 |
Нетрудно убедиться, что после каждого выполнения п. 8 множество E1 является множеством минимальных по весу ребер для леса Т, рассматриваемого в этот момент. Поэтому согласно утверждению 75.2 граф Т' = Т + Е1 снова является остовным лесом. Это означает,
что алгоритм строит некоторый остов графа G. Минимальность этого остова доказывается с помощью теоремы 75.1 точно так же, как при обосновании предыдущего алгоритма.
Выясним теперь быстродействие алгоритма A4. Для однократного выполнения каждого из пп. 3—6 достаточно времени O(1) и, следовательно, построение Е1 осуществляется за время O(|EG|). Таких же затрат достаточно и для однократного выполнения пп. 8—11. Таким образом, затраты на переход от Т к Т' = Т + Е1 (т. е. на выполнение одной итерации) составляют O(|EG|) операций. Оценим теперь число итераций алгоритма. Поскольку одно ребро может быть минимальным по весу не более чем для двух компонент леса Т, то на каждой итерации |Е1| ≥ р(Т)/2.А так как Т + Ех — лес,то р(Т+ Е1< <р(Т)/2, т. е. на каждой итерации число компонент уменьшается по крайней мере вдвое. Это означает, что число итераций алгоритма не превосходит log |G|, следовательно, он строит минимальный остов за время O(|EG|log|G|).
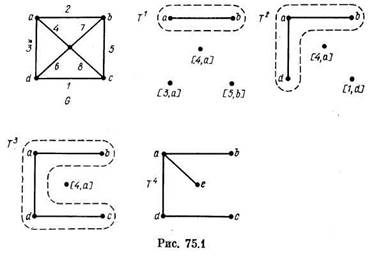
Пример 2. Применим алгоритм A4 к графу, изображенному на рис. 75.2. На первой итерации будет найдено множество Е1 = { а1a2 ,а1a3 ,а4 a7 ,а5 a8 ,а6 a9 ,а9 a10 } минимальных по весу ребер для леса, имеющего одновершинные компоненты. Остовные леса, полученные в результате выполнения 1-й, 2-й и 3-й итераций, изображены на рис. 75.3. Последний из них является минимальным остовом.
Кратчайшие пути
Пусть G=(V, A)—ориентированный взвешенный граф. Задача о кратчайшем пути состоит в отыскании пути минимального веса, соединяющего заданные начальную и конечную вершины графа G при условии, что хотя бы один такой путь существует. Начальную и конечную вершины обозначим соответственно через s и t; (s, t)-путь минимального веса будем называть кратчайшим (s, t)-путем.
Вначале рассмотрим случай, когда веса всех дуг графа неотрицательны, т. е. w(e) ≥ 0 для каждой дуги е € А. В этом случае решение задачи о кратчайшем пути является существенно менее трудоемким, чем в общем случае. Первый эффективный алгоритм построения кратчайшего пути в графе с неотрицательными весами дуг предложил Е. Дийкстра в 1959 г.
На каждой итерации этого алгоритма всякая вершина и графа G имеет метку l(v), которая может быть постоянной либо временной. В первом случае l(v) — вес кратчайшего (s, v)-пути. Если же метка l(v) временная, то l(v)—вес кратчайшего (s, v)-пути, проходящего только через вершины с постоянными метками. Таким образом, временная метка l(v) является оценкой сверху для веса кратчайшего (s, v) -пути, и став на некоторой итерации постоянной, она остается такой до конца работы алгоритма. Кроме l(v), с каждой вершиной v графа G, за исключением s, связывается еще одна метка— θ(v). На каждой итерации θ(v) является номером вершины, предшествующей v в (s, v) -пути, имеющем минимальный вес среди всех (s, v) -путей, проходящих через вершины, получившие к данному моменту постоянные метки. После того как вершина t получила постоянную метку, с помощью меток θ(v) легко указать последовательность вершин, составляющих кратчайший (s, t)-путь.
Перед началом первой итерации алгоритма вершина s имеет постоянную метку l(s)=0, а метки l всех остальных вершин равны ∞ и эти метки временные. Общая итерация алгоритма состоит в следующем. Пусть р — вершина, получившая постоянную метку l(р) на предыдущей итерации. Просматриваем все вершины v € Г(р), имеющие временные метки, с целью уменьшения (если это возможно) этих меток. Метка l(v) вершины Г(p) заменяется на l(p)+w(p, v), если оказалось, что l(v)>l(p)+ w(p, v). В этом случае говорим, что вершина v получила свою метку l из вершины p, и полагаем θ(v) = p. Если же l(v) ≤ l(p)+ w(p, v), то метки θ и l вершины v не изменяются на данной итерации. Алгоритм заканчивает работу, когда метка l(t) становится постоянной. Как уже говорилось выше, l(t)—вес кратчайшего (s, t)-пути, который будем обозначать через Р*. Этот
 |
путь определяется с помощью меток θтак:
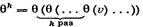 где для любой вершины v € VG.
где для любой вершины v € VG.
Будем считать, что граф G задан матрицей весов либо списками смежности.
Алгоритм A5 Дийкстры поиска кратчайшего пути.
1. Положить l(s): = 0 и считать эту метку постоянной. Положить l(v):=∞ для всех v € VG,
v≠s, и считать эти метки временными. Положить р := s.
2.
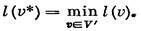 |
Для всех v € Г(p) с временными метками выполнить: если l(v)> l(p)+ w(p, v), то l(p):= l(p) + w(p, v) и θ(v) := p. Иначе l(v) и θ(v) не менять.
3. Пусть V’ — множество вершин с временными метками l. Найти вершину v*, такую что
Считать метку l(v*) постоянной меткой вершины v*.
4. p:=v*. Если p = t, то перейти к п. 5 [l(t)—вес кратчайшего пути]. Иначе перейти к п. 2.
5. P*:=(s, ..., θ3(t), θ2(t), θ(t), t) [P*- кратчайший путь]. Конец.
Прежде чем перейти к обоснованию алгоритма, сделаем три полезных замечания.
Замечание 1. Как легко видеть, алгоритм A5 применим к смешанным и, в частности, к неориентированным графам. Для этого достаточно каждое неориентированное ребро uv графа, имеющее вес w(u, v), рассматривать как пару дуг (и, v) и (v, и) того же веса.
Замечание 2. Если п. 4 модифицировать так, чтобы алгоритм заканчивал работу только после получения всеми вершинами постоянных меток, то он будет строить кратчайшие пути из s в каждую из остальных вершин. Если к тому же вместе с превращением метки вершины v* в постоянную (п. 3 алгоритма) заносить дугу (θ(v*), (v*) в множество А*, то после окончания работы алгоритма граф D=(VG, А*) будет корневым ориентированным остовным деревом. Это дерево называют деревом ратчайших путей из s графа G. Для любой вершины v € VG единственный (s, v)-путь в дереве D является кратчайшим (s, v) -путем в графе G.
Замечание 3. Алгоритм A5, модифицированный так, как указано в замечании 2, можно рассматривать как алгоритм построения дерева D кратчайших путей из вершины s графа G. С этой точки зрения алгоритм A5 аналогичен алгоритму A3 построения минимального остова. Действительно, построение дерева D состоит в последовательном увеличении уже построенного фрагмента путемдобавления некоторой дуги, «выходящей» из этого рагмента. При этом метки l и θ играют такую же роль, как и метки α и β в алгоритме A3.
Утверждение 76.1. Алгоритм A5 строит в графе кратчайший (s, t)-путь за время O(|G|2). Заметим вначале, что метка вершины v (l(v)≠∞) равна весу (s, v)-пути, который построен алгоритмом к тому моменту. Он определяется метками θ, имеющимися в заданный момент. Поэтому для доказательства оптимальности (s, t)-пути, соответствующего постоянной метке l(t), достаточно доказать, что постоянная метка l(v) каждой вершины v равна весу кратчайшего (s, v)-пути. Это утверждение будем доказывать по индукции. Пусть вершина v получила свою постоянную метку на k-й итерации, т. е. после k-говыполнения п. 3. При k = 1 справедливость утверждения очевидна. Предположим, что оно верно для вершин, получивших свои постоянные метки на итерациях 2, 3, ..., k — 1. Обозначим через Р° (s, v)-путь, построенный алгоритмом в результате k итераций, а через Р* — кратчайший (s, v)-путь. По условию w(P°)= l(v). Пусть V1 и V2 — множества вершин, имеющих соответственно постоянные и временные метки перед началом k-йитерации. Рассмотрим две возможные ситуации:
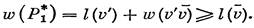 |
а) Путь Р* содержит вершины из V2. Пусть v — первая (считая от s)такая вершина, принадлежащая Р*,а вершина v' предшествует v на пути Р*, т. е. (v', v) € АР*. Согласно выбору v имеем v' € V1. Обозначим через P1* часть пути Р* от s до v. По предположению индукции l(v')— вес кратчайшего (s, v') -пути. Поэтому
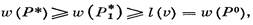 |
Поскольку l(v)—временная метка, а постоянная метка l(v) вершины v выбирается на k-йитерации как наименьшая из временных, то l(v’) ≥ l(v). Объединив это неравенство с (1), получим
т. е. Р° — кратчайший (s, v) -путь.
 |
б) Все вершины пути Р* входят в V1. Пусть v' и v" — такие вершины, что (v', v) € AP* и (v", v) € AP°.Обозначив через Р' часть пути Р* от s до v', согласно предположению индукции имеем w(P') ≥ l(v'). Поэтому,если v' = v", то сразу получаем неравенство
 |
Допустим теперь, что v' ≠ v". Поскольку v получает постоянную метку l(v) из v", а не из v', то
Таким образом, и в случае б) верно неравенство w(P0) ≤ w(P*), т. е. Р° — кратчайший (s, v)-путь.
Оценим теперь трудоемкость алгоритма. Вычислительные затраты максимальны, когда вершина t получает постоянную метку последней и граф G является полным. В этом случае число итераций алгоритма равно |G| — 1, т. е. каждый из пп. 2—4 выполняется |G| - 1 раз. Очевидно, что п. 4 выполняется за время O(1), а для выполнения каждого из пп. 2, 3 достаточно времени O(|G|).
построение пути с помощью меток θ можно осуществить, потратив не более O(|G|) операций. Таким образом, вцелом время построения кратчайшего (s, t) -пути не превосходят O(|G|2).
Пример 1. На рис. 76.1 изображены пятькопий Gk(k — 1,5) графа G, каждая из которых отражает ситуацию, сложившуюся после очередной итерации алгоритма. Около каждой дуги написан ее вес. Вершинам копии Gk (k = 1, 5) приписаны метки, полученные ими в результате выполнения первых k итераций. Некоторые дуги обведены жирными линиями, т. е. отмечены. Добавление такой дуги (а, b) при переходе от Gk к Gk+1 означает, что вершина b получила свою метку l(b) из а и эта метка стала постоянной на (k+1)-йитерации. Вершина t в нашем примере получает постоянную метку последней, и отмеченные дуги Gs образуют дерево кратчайших путей из s.
При решении многих задач возникает необходимость отыскания в невзвешенном графе (s, t)-пути с минимальным количеством дуг. Такой путь, очевидно, можно найти с помощью алгоритма Дийкстры. Для этого достаточно присвоить всем дугам графа G веса, равные 1, и применить алгоритм A5. Проследим работу алгоритма в этой ситуации, обращая особое внимание на последовательность, в которой вершины графа G получают постоянные метки. Очевидно, что вначале постоянные метки l=1 получат все вершины множества Г (s). Затем метка l = 2 будет присвоена концам дуг, выходящих из Г (s). Вообще, постоянную метку l=k получают еще не помеченные вершины, являющиеся концами дуг, исходящих из вершин с метками l= k - 1. Этот процесс обхода (и присвоения меток) вершин графа называют поиском в ширину в графе (на интуитивном уровне поиск в ширину описан в § 9). По окончании поиска в ширину метка l(х) вершины х равна минимальному числу дуг в (s, x)-пути. Как и ранее, сам этот путь определяется метками θ. Осуществление поиска в ширину с помощью алгоритма Дийкстры связано, как мы знаем, с вычислительными затратами O(|G|2).
Рассмотрим алгоритм A6, осуществляющий поиск в ширину за время O(|EG|). В этом алгоритме метки l и θ играют ту же роль, что и в предыдущем, с той, однако, разницей, что метки l не делятся на временные и постоянные. Как только вершина х получает метку l(х)≠∞, эта метка сразу становится постоянной (т. е. окончательной). За счет этого, в частности, достигается экономия времени вычислений по сравнению с алгоритмом Дийкстры.
Особую роль в алгоритме A6 играет список Q. Каждая вершина графа один раз заносится в этот список иодин раз из него вычеркивается. При этом вычеркивается все время первая (на данный момент) вершина этого списка, а только что добавленная вершина всегда является последней в списке, т. е. Q — очередь. Вначале в Q находится единственная вершина s, l(s)=0, а все остальные вершины меток не имеют. Общая итерация состоит в следующем. Выбирается первая вершина х в списке Q. Каждой непомеченной вершине у €Г(х) присваиваются метки l(у)= l(х)+ 1 и θ(y)=x, после чего вершина у становится последней в списке Q, а вершина х удаляется из Q. Алгоритм прекращает работу, как только в Q не останется ни одной вершины. При этом вершины, достижимые из s, будут иметь метки, а недостижимые — нет. Для быстрого выполнения операций вычеркивания и включения элементов в Q используются переменные указатели р и q — адреса первой ипоследней занятых ячеек списка Q соответственно.
Будем считать, что граф G задан списками смежности и Nv — список, содержащий концы всех дуг, исходящих из вершины v.Алгоритм A6 поиска в ширину.
1. Q (1):=s, p:=1, q:=1, l(s):=0.
2. х := Q(p), m := |Г(х)|I [выбрана первая вершина х очереди Q].
[Пп. 3—5 — присвоение меток непомеченным вершинам из Т(х)].
3. k:=1.
4. Если вершина у = Nx(k) имеет метку, то перейти к п. 5. Иначе l(y):= 1(х)+ 1, θ(y):=x, q:=q+1,Q(q):=y [вершина у помечена и включена в очередь Q]и перейти к п. 5.
5. Если k= т, то перейти к п. 6, иначе k:=k + 1 и перейти к п. 4.
6. р := р + 1 [вершина х исключена из Q].
7. Если р> q, то конец [Q = ¢, т. е. все вершины,достижимые из s, получили метки], иначе перейти к п. 2.
Утверждение 76.2. Алгоритм A6 присваивает метки l и θ всем вершинам графа, достижимым из вершины s за время O(|EG|). При этом (s, ..., θ3(x), θ2(x), θ(x), х) — (s, х)-путь с минимальным числом дуг, а l(х)— число дуг в этом пути.
 Основные вычислительные затраты связаны с выполнением п. 3 алгоритма. Суммарное время выполнения этого пункта составляет , поскольку каждый из списков Nv просматривается в точности один раз. Затраты на выполнение других пунктов, очевидно, не превосходят этой величины.
Основные вычислительные затраты связаны с выполнением п. 3 алгоритма. Суммарное время выполнения этого пункта составляет , поскольку каждый из списков Nv просматривается в точности один раз. Затраты на выполнение других пунктов, очевидно, не превосходят этой величины.
Выше отмечалось, что результаты алгоритма A6 (т. е. метки l и θ) те же, что и в алгоритме Дийкстры, если каждой дуге графа G приписать вес, равный 1. Поэтому справедливость второго утверждения следует из утверждения 76.1.
Замечание 4. Иногда требуется искать пути из вершин множества X € VG во все остальные вершины. Для решения этой задачи достаточно слегка модифицировать алгоритм A6 изменив в нем п. 1. Именно, в список Q следует поместить все вершины множества X и положить l(х)=0 для каждой вершины х € Х. На модифицированный таким образом алгоритм A6 будем ссылаться как на поиск в ширину из множества X.
Перейдем теперь к рассмотрению общей ситуации, Будем считать, что в графе G допускаются дуги отрицательного веса. Предлагаемый ниже алгоритм A7 строит в таком графе кратчайшие пути между всеми парами вершин графа при условии, что в графе нет отрицательных контуров (контуров отрицательного веса). Если же такой контур в графе имеется, то алгоритм сообщает об этом и прекращает работу, оставляя задачу отыскания кратчайшего пути нерешенной (см. ниже замечание 6). Будем считать, что граф G, |G|=n, задан матрицей весов W = |Wij|, т. е. Wij = w(i, j), если (i, j) € AG, и Wij=∞ в противном случае. Кроме того, полагаем Wu = 0 для всех i=l, 2, ..., п. Алгоритм основан на следующих соображениях. Пусть i, j, k — три любые вершины графа G, и мы хотим получить (i,j)-путь, кратчайший среди (i,j)-путей, не содержащих внутренних вершин, отличных от k. Очевидно, что для этого достаточно выбрать меньшую из двух величин Wij и Wij+ Wkj, которая и будет весом такого (i,j)-пути. Если зафиксировать k и проделать эту операцию (назовем ее t-операцией, примененной к индексу k) для всех пар (i, j), то получим матрицу W = ||W’ij||. У которой W’ij= min {Wij, Wik + Wkj}. Оказывается (это будет позднее доказано), имея матрицу Ws весов кратчайших путей, проходящих только через вершины множества S € VG, можно получить такую же матрицу для путей, проходящих через множество S U {m}, m¢ S. Для этого достаточно применить t-операцию к индексу т ивсем элементам матрицы Ws. Именно в этом и состоит итерация алгоритма A7, который, начиная с W° = W, строит такую последовательность матриц W°, W1, ..., Wn, что Wm получается из Wm-1 применением t-операции к индексу ти матрице Wm-1. Если в графе G нет отрицательных контуров, то элемент Wijm матрицы Wm при каждом травен весу кратчайшего (i, j)- пути, все внутренние вершины которого принадлежат множеству {1, 2, ..., т}. Таким образом, последняя из этих матриц, Wn, содержит веса кратчайших путей между всеми парами вершин графа. Для того чтобы после окончания работы алгоритма иметь возможность быстро найти кратчайший путь между любой парой вершин, будем на k-йитерации вместе с матрицей Wk строить матрицу Рk = | |Pij||. Вначале полагаем Pij0 = i(i,j= 1, п). Далее, на k-йитерации полагаем Pijk= Pijk-1если Wijk = Wijk-1 и Pijk= Pkjk-1, если Wijk = Wikk-1 + Wkjk-1. Таким образом, Pijk —номер вершины, предшествующей вершине j в текущем (i, j)- пути, т. е. в кратчайшем (i, j)- пути, все внутренние вершины которого содержатся в множестве (1, 2, ..., k). Матрица Рп = || Pijn || играет ту же роль, что и метки θ в предыдущих алгоритмах A5 и A6. С помощью этой матрицы кратчайший (i, j)- путь L(i, j) определяется следующим образом: L(i, j) = (i, ..., j3, j2, j1, j), где j1 = Pijn, j2 = Pij1n, j3 = Pij2n
Алгоритм A7 отыскания кратчайших путей между всеми парами вершин.
1. W0:=W, k:=1, P°:= ||Pij0|| где Pij0=i если Wij ≠ ∞, и Pij0 =0 в противном случае.
2. Выполнить для всех (i, j)=1,n если Wijk-1< Wikk-1 + Wkjk-1, то Wijk = Wijk-1 , Pijk= Pijk-1. Иначе Wijk := Wikk-1 + Wkjk-1, Pijk := Pkjk-1 .
3. Если для некоторого l, 1≤ l ≤ n, то конец [в графе имеется отрицательный контур]. Иначе перейти к п. 4.
4. k:=k+1. Если k = n +1, то конец [Wn= || Wijn || —матрица весов кратчайших путей, определяемых с по мощью матрицы Рп = || Pijn ||].
Замечание 5. Алгоритм будет применим к смешанным графам, если каждое неориентированное ребро заменить на две дуги того же веса (см. замечание 2).При этом следует учесть, что неориентированное ребро отрицательного веса сразу приводит к отрицательному контуру.
Замечание 6. Алгоритм «отказывается» строить кратчайшие пути, когда в графе G имеются отрицательные контуры. В этом случае задача отыскания кратчайшего пути между двумя вершинами (или между всеми парами вершин) остается корректной, но становится очень трудной. Можно показать, что она не менее трудна, чем, например, задача о коммивояжере.
Перейдем теперь к обоснованию алгоритма A7 и оценке его трудоемкости.
Утверждение 76.3. Пусть взвешенный ориентированный мулътиграф L имеет эйлерову цепь, соединяющую вершины а и b. Если в L нет отрицательных контуров, то в нем имеется такой (а, b)-путъ Р, что
w(L) ≥ w(P).
 |
Будем считать, что мультиграф L не является путем (иначе утверждение тривиально). Поэтому он содержит некоторый контур S. Удалив из L все дуги этого контура, получим мультиграф L'. Поскольку w (S) ≥ 0, то w(L) ≥ w(L'). Кроме того, согласно теореме 65.2 полустепени вершин мультиграфа V удовлетворяют соотношениям
Поэтому вершины а и b принадлежат одной его слабой компоненте L", и последняя содержит эйлерову (а, b)-цепь. Продолжая подобным образом, получим требуемый (а, b)-путь.
Утверждение 76.4. Если в графе нет отрицательных контуров, то при всех k, i, j = 1, п. Wijk — вес кратчайшего (i, j)-пути, все внутренние вершины которого содержатся в множестве {1, 2, ..., k}.
Доказываем индукцией по k. При k = 1 справедливость утверждения очевидна. Предположим, что оно справедливо для 2, 3, ..., k— 1, и рассмотрим Wijk. Пусть Р° — кратчайший (i,j)-путь, все внутренние вершины которого принадлежат множеству {1, 2, ..., k}. Если Р° не включает вершину k, то Wijk = Wijk-1 и, согласно предположению индукции, w(P°) = Wijk-1 = Wijk. Допустим теперь, что Р° содержит вершину k. Обозначим через P10 и P20 части пути Р° от i до k и от k до j соответственно. Предположим, что один из этих путей, например P10, не является кратчайшим, и пусть Р' — кратчайший (i, k)-путь, все вершины которого содержатся в множестве {1, 2, ..., к - 1}. Рассмотрим мультиграф L, получающийся из графа Р' U P20 заменой каждой дуги, входящей одновременно в Р' и P20, двумя экземплярами этой дуги. Очевидно, что L не содержит отрицательных контуров. Поэтому, согласно утверждению 76.3, L содержит такой (i, j)-путь Р, что w(L) ≥ w(P) и, следовательно, w(P°) = w(P10) + w(P20) > w(P') + w (P20) = w(L) ≥ w(P). Это неравенство противоречит минимальности Р°.
 |
Таким образом, пути P10 и P20 являются кратчайшими среди, соответственно, (i, k)- и (к, j)-путей, все внутренние вершины которых принадлежат множеству {1,2,...,k-1). Поэтому, воспользовавшись предположением индукции, получим
Теорема 76.5. Время работы алгоритма A7 не превосходит O(|G|3). Если граф G не содержит отрицательных контуров, то Wijn — вес кратчайшего (i, j)-пути в графе G для всех i, j = 1, п, п=|G|. Если же такие контуры в графе имеются, то существуют такие числа т. иl,что Wllm <0.
Справедливость первого утверждения теоремы очевидна, поскольку каждая из не более чем |G| итераций выполняется за время O|G|2.
Второе утверждение теоремы непосредственно следует из утверждения 76.4.
Допустим теперь, что граф G содержит отрицательные контуры. Пусть m — такой наименьший индекс, что для некоторой вершины l в графе G имеется отрицательный контур S, содержащий только l и некоторые вершины множества (1, 2, ..., m). Ясно, что контур S включает вершину т. Тогда при любых i,j = 1, п число Wijm-1 равно весу кратчайшего (i, j)-пути, все внутренние вершины которого принадлежат множеству {1, 2, ..., m—1}. Доказательство этого факта дословно повторяет доказательство утверждения 76.4. Контуру S соответствуют (l, m)-путь P1 и (т, 1)-путь P2, такие, что P1U P2 = S. Поскольку внутренние вершины путей P1 и P2 принадлежат множеству {1, 2, ..., m-1}, то w(P1)≥ Wmlm-1 , w(P2) ≥Wlmm-1. Следовательно, Wmlm-1 + Wlmm-1≤ w (Р1) + w(P2) = w(S), т. е. Wllm = min {0, Wmlm-1 + Wlmm-1}< 0.
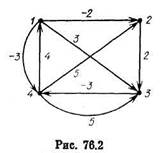 |
Пример 2. Ниже приведены результаты выполнения каждой из четырех итераций алгоритма для графа, изображенного на оис. 76.2:

Найдем, например, с помощью матрицы Р4 кратчайший (2 1)-путь: P214 = 4, P244 = 3, P
Дата добавления: 2019-07-26; просмотров: 645;
