Теоретические сведения
Бинарным отношением между элементами множеств А и В называется любое подмножество R Í A´B. Если множества A и B совпадают А = В, то R называют бинарным отношением на множестве А. Всюду далее будут рассматриваться такие отношения. Если (x, y)ÎR, то это обозначают еще xRy и говорят, что между элементами x и y установлено бинарное отношение R.
Способы задания бинарных отношений.
1. Матричное задание. Пусть А – конечное или счетное множество А = {xi}. Тогда бинарное отношение R задаётся матрицей R = {rij}, элементы которой определяются соотношением:
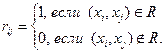
2. Задание с помощью графа.
Для конечного или счетного множества А отношение можно задавать с помощью графа Г(R), который является геометрическим образом бинарного отношения. Граф – фигура состоящая из точек (вершин) соединенных линиями (дугами). Вершины графа соответствуют элементам множества А, то есть xi, а наличие дуги, соединяющей вершины xi и xj, означает, что (xi, xj)ÎR. Чтобы подчеркнуть упорядоченность пары на дуге ставится стрелка.
3. Задание верхними и нижними срезами – универсальный способ задания бинарного отношения для любых множеств. Верхний срез GR(x) отношения R в точке x ÎА
GR(x) = { yÎA | (y, x)ÎR }.
Нижний срез HR(x) отношения R в точке xÎА
HR(x) = { yÎA | (x, y)ÎR }.
Запишем кратко свойства бинарных отношений и условия, которым должна удовлетворять матрица бинарного отношения, удовлетворяющего этому свойству.
1) Рефлексивность. Бинарное отношение рефлексивно, если
.
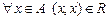Следовательно, матрица рефлексивного бинарного отношения R на главной диагонали содержит только единицы.
2) Антирефлексивность. Бинарное отношение антирефлексивно, если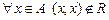 
.
Следовательно, матрица антирефлексивного бинарного отношения R на главной диагонали содержит только нули.
3) Симметричность. Бинарное отношение симметрично, если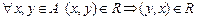 
.
Матрица симметричного бинарного отношения R симметрична относительно главной диагонали, причём на главной диагонали могут находиться любые допустимые значения. То есть у матрицы такого бинарного отношения не должно быть различных симметричных элементов (симметрия здесь и всюду далее рассматривается относительно главной диагонали) вне главной диагонали, так как элемент главной диагонали всегда совпадает сам с собой.
4) Асимметричность. Бинарное отношение асимметрично, если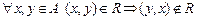 
.
Матрица асимметричного бинарного отношения R не должна содержать симметричных единиц, включая главную диагональ, то есть на главной диагонали должны находиться нули.
5) Антисимметричность. Бинарное отношение асимметрично, если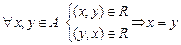 
.
Матрица антисимметричного бинарного отношения R также не содержит симметричных единиц вне главной диагонали, но на главной диагонали могут находиться произвольные допустимые значения.
6) Транзитивность. Бинарное отношение транзитивно, если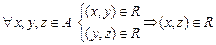 
.
Данное свойство не формулируется в терминах симметричных относительно главной диагонали элементов, в нём рассматриваются различные тройки элементов матрицы, имеющие индексы, соответствующие условию транзитивности. Если первые два элемента тройки равны 1, то третий не может быть 0.
7) Негатранзитивность. Бинарное отношение R негатранзитивно, если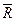 
транзитивно, т.е.
.
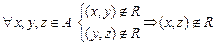Аналогично свойству транзитивности, если первые два элемента тройки равны 0, то третий не может быть 1.
8) Полнота. Бинарное отношение полно, если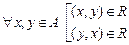 
.
У матрицы полного бинарного отношения не может быть симметричных нулей, включая главную диагональ.
9) Слабая полнота. Бинарное отношение слабо полно, если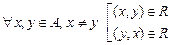 
.
Аналогично предыдущему свойству, у матрицы слабо полного бинарного отношения не может быть симметричных нулей вне главной диагонали, а элементы главной диагонали могут быть произвольными.
Дата добавления: 2017-02-20; просмотров: 879;