Пример выполнения работы.

1. Даны множества; 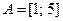, , 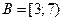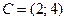. Найти:

a) ;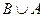

b) ;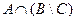

Даны множества; 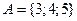, , 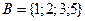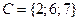. Найти:

c) ;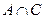

d) .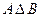

Решение.

a) 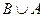= [1; 7)

b) 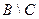= [4; 7) 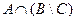= [4; 5]

c) 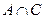= Æ

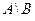d) = {4} 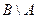= {1; 2} 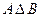= {1; 2; 4}

2. Доказать тождество AÇ(B \ C) = (AÇB) \ (AÇC).

Решение.

a) I способ. Докажем два нестрогих включения.

1) Прямое включение AÇ(B \ C) Í (AÇB) \ (AÇC).

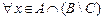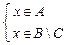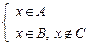Þ 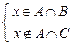Þ Þ Þ Þ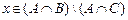

2) Обратное включение (A ÇB) \ (AÇC) Í AÇ(B \ C).

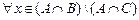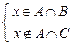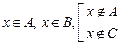Þ Þ Þ Þ 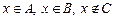, так как в 1-м случае имеем противоречие 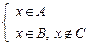Þ Þ 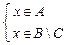Þ Þ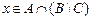

b) II способ.

(AÇB) \ (AÇC) = 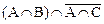= = 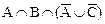= = = = 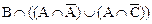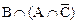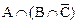AÇ(B \ C)

3. Доказать включение множеств

(A₁ Ç A₂) D (B₁ Ç B₂) Í (A₁ D B₁) È (A₂ D B₂).

Решение.

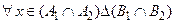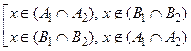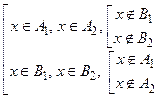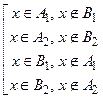Þ Þ

Þ 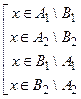Þ Þ Þ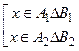

Þ Þ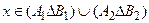

4. Доказать, что A Í B Ç C Û A Í B и A Í C.

Решение.

1) Докажем прямое следование, т.е. AÍBÇC Þ AÍB и AÍC.

Пусть справедливо включение 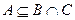, покажем, что AÍB и

AÍC.

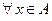
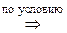
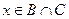
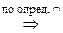
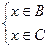
Что и означает выполнение обоих включений .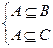

2) Докажем обратное следование AÍB и AÍC Þ AÍBÇC.

Пусть выполнены оба включения 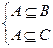, покажем, что AÍBÇC.

.

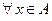
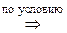
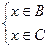
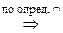
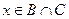Следовательно .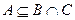

Контрольные вопросы

1. Дайте определения операций дополнения, пересечения, объединения, разности и симметричной разности множеств. Приведите примеры выполнения операций.

2. Сформулируйте отрицание принадлежности элемента множествам, построенных с помощью операций над множествами.

3. Приведите способы доказательства отношений нестрогого, строгого включения и равенства множеств.