Операции над нечеткими множествами

Подобно операциям над четкими множествами, нечеткие множества также можно пересекать, объединять и инвертировать. Л. Заде предложил оператор минимума для пересечения и оператор максимумадля объединения двух нечетких множеств. Видно, что эти операторы совпадают с объединением и пересечением, если мы рассматриваем только степени принадлежности 0 и 1.

1 ОПЕРАЦИЯ ОБЪЕДИНЕНИЯ

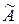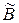Объединением нечетких множеств и называется множество:

,

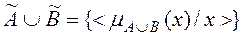где

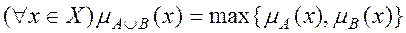
Предположим, на интервале от [0; 0,4] функция принадлежности (ФП) описывается выражением 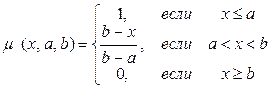(1):

(1)

Графическое изображение функции (1) при a=0 и b=0,4 приведено на рисунке 29.

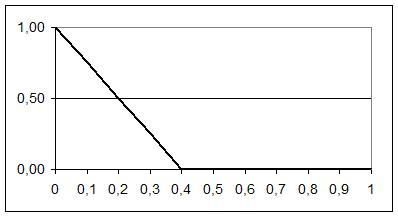
Рисунок 29 – ФП для выражения (1)

Предположим, на интервале [0,2; 0,8] функция принадлежности описывается выражением 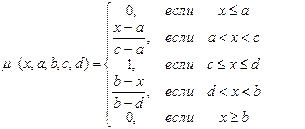(2):

(2)

Графическое изображение функции (1) при a=0,2; c=0,3; d=0,7; b=0,8 приведено на рисунке 30.

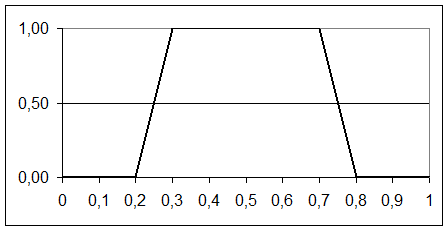
Рисунок 30 – ФП для выражения (2)

Тогда в результате выполнения операции объединения общий вид ФП будет такой (рисунок 31).

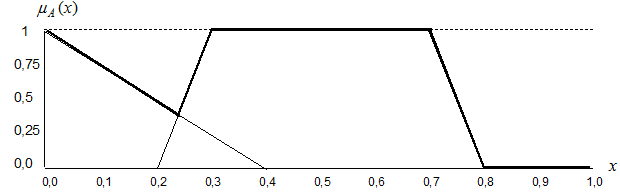
Рисунок 31 – Результат выполнения операции объединения

2 ОПЕРАЦИЯ ПЕРЕСЕЧЕНИЯ

Пересечением нечетких множеств Ã и B̃ называется множество:

,

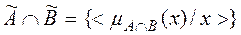где

.

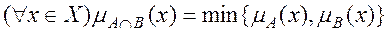Для условий предыдущего примера результат операции пересечения будет иметь вид (рисунок 32):

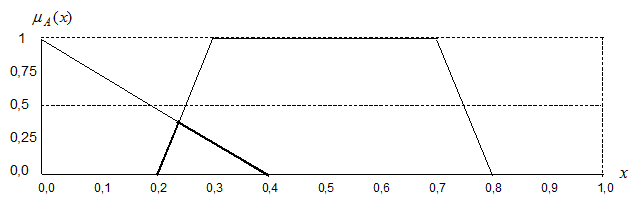
Рисунок 32 – Результат выполнения операции пересечения

3 ОПЕРАЦИЯ ДОПОЛНЕНИЯ

Дополнением нечеткого множества Ã называется множество

,

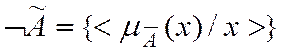где

.

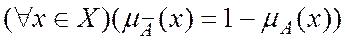Носителем нечёткого множества ̃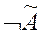 будет являться множество 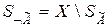, т. е. множество тех элементов , для которых функция принадлежности .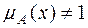

Предположим, на интервале от [0,1; 0,5] функция принадлежности описывается выражением (3):

(3)

Графическое изображение функции (3) при a=0,1 c=0,3 и b=0,5 приведено на рисунке 33. На этом же рисунке приведена и функция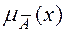

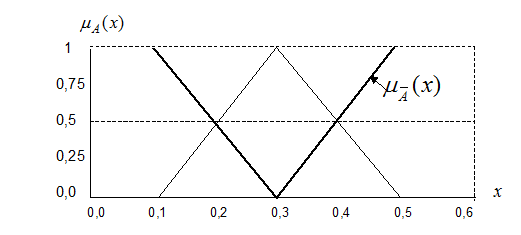
Рисунок 33 – Результат выполнения операции дополнения