ПОСТРОЕНИЕ ФУНКЦИИ ПРИНАДЛЕЖНОСТИ ОДНИМ ЭКСПЕРТОМ
Рассмотрим нечеткое понятие "возраст". Определим «возраст» как лингвистическую переменную (ЛП). Базовый набор значений ЛП "возраст" определим как (рисунок 2):
В - {младенческий, детский, юный, молодой, зрелый, преклонный, старый}
Для ЛП "возраст" базовая шкала – это числовая шкала от 0 до 120, обозначающая количество прожитых лет, а функция принадлежности определяет, насколько мы уверены в том, что данное количество лет можно отнести к данной категории возраста. На рисунке 6 отражено, как одни и те же значения базовой шкалы могут участвовать в определении различных нечетких множеств (НМ).
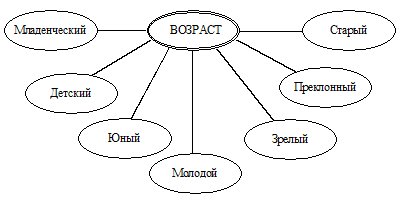
Рисунок 5 – Базовый набор значений ЛП "возраст"
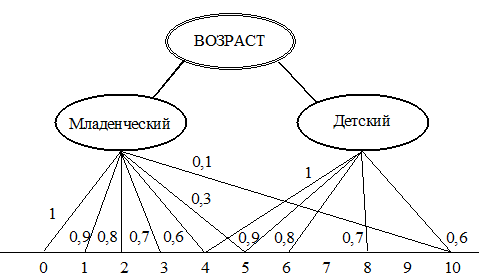
Рисунок 6 – Базовая шкала ЛП "возраст"
Например, определить значение НМ "младенческий возраст" можно так.
Рисунок 7 иллюстрирует оценку НМ экспертом, который ребенка до полугода с высокой степенью уверенности относит к младенцам (m = 1). Дети до четырех лет причисляются к младенцам тоже, но с меньшей степенью уверенности (0,5< m <0,9), а в десять лет ребенка называют так только в очень редких случаях – к примеру, для девяностолетней бабушки и 15 лет может считаться младенчеством.
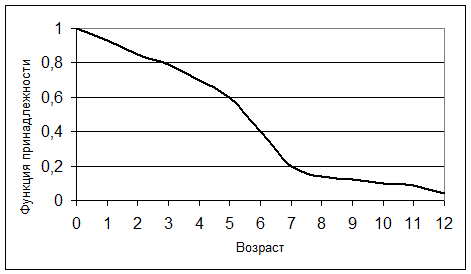
Рисунок 7 – Функция принадлежности терма лингвистической
переменной "младенческий возраст"
ПОСТРОЕНИЕ ФУНКЦИИ ПРИНАДЛЕЖНОСТИ С ИСПОЛЬЗОВАНИЕМ
МЕТОДА ЭКСПЕРТНОЙ ОЦЕНКИ
С помощью функции принадлежности можно отразить мнение одного или нескольких экспертов. Это связано с неспособность человека формулировать свое количественное впечатление в виде однозначного числа. Предположим, что имеется m экспертов, часть из которых на вопрос о принадлежности элемента хÎХ нечеткому множеству А отвечает положительно. Обозначим их число n1. Другая часть экспертов n2 = m – n1 отвечает на этот вопрос отрицательно. Тогда принимаем, что функция принадлежности может быть описана выражением
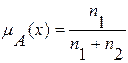 . (10)
. (10)
Пример. Пусть имеется множество Х={1, 2, 3, 4, 5, 6} и требуется построить нечеткое множество А формализующее нечеткое понятие "намного больше двух". Решение задачи может выглядеть так. Допустим, что результаты опроса шести экспертов дали такие результаты (таблица 1). Причем если на вопрос о принадлежности элемента хÎХ нечеткому множеству А эксперт отвечает положительно, то в таблицу заносим знак "+", если отрицательно, то знак " – ". Обозначим число положительных знаков как n1, а число отрицательных знаков как n2 = m – n1.
Таблица 1 – Результат опроса экспертов
| Эксперты | Х | |||||
| – | – | – | + | + | + | |
| – | – | – | + | + | + | |
| – | – | + | + | + | + | |
| – | – | – | – | – | + | |
| – | – | – | – | + | + | |
| – | – | – | + | + | + | |
| n1= | ||||||
| n2= |
Используя формулу (1), определяем функцию принадлежности:
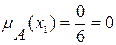 ;
;  ;
;  ;
;
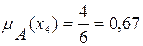 ;
; 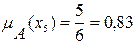 ;
; 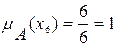 .
.
Тогда формальная запись нечеткого множества А будет такой:
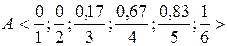

Рисунок 8 – Функция принадлежности для примера
1 МЕТОДИКА ПОСТРОЕНИЯ ФУНКЦИИ ПРИНАДЛЕЖНОСТИ
Методику построения функции принадлежности (ФП) рассмотрим на модельном примере: "Определить семантику и термы лингвистической переменной "Вероятность". Методика решения задачи предусматривает выполнение этапов:
1 этап. Определение термов лингвистической переменной (ЛП).
В нашем случае это могут быть, например, "Вероятность большая"; "Вероятность средняя"; "Вероятность малая".
2 этап. Ранжирование термов.
В данном случае можно выполнить ранжирование типа "по возрастанию". Таким образом, результатом выполнения этапа будет последовательность:
1 – "Вероятность малая"; 2 – "Вероятность средняя"; 3 –"Вероятность большая".
3 этап. Определение интервалов термов (то есть назначение левой и правой границ интервала). В каждом конкретном случае эти границы будут различны. В нашем примере лингвистическая переменная "Вероятность" имеет крайнюю левую границу 0, а крайнюю правую – 1 (по своей сути вероятность меняется от 0 до 1, т.е. вероятность невозможного события равна 0, а вероятность достоверного события равна 1). Промежуточные значения выбираются на основе субъективного суждения. Предположим, что граничные пары значений термов установлены такими, как представлены в таблице 2.
Таблица 2 – Левая и правая границы интервалов термов
| Номер и наименование терма | Левая граница | Правая граница |
| 1 "Вероятность малая" | 0,4 | |
| 2 "Вероятность средняя" | 0,2 | 0,8 |
| 3 "Вероятность большая" | 0,6 | 1,0 |
4 этап.Графическое изображение установленных границ интервалов термов (рисунок 9).
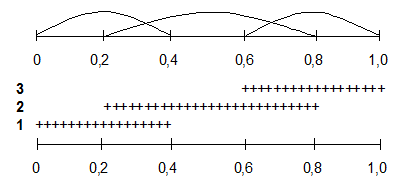
Рисунок 9 – Границы интервалов
5 этап. Корректировка границ интервалов термов (необязательный этап).
6 этап.Выбор метода построения ФП. В данном примере используем метод деления значений ФП пополам.
7 этап.Определение семантики терма лингвистической переменной.
7.1 Рассмотрим 1 терм: "Вероятность малая". Для него определим значения ФП в граничных точках интервала. В граничной точке 0,0 ФП равна 1, так как если вероятность равна нулю, то она естественно малая и ФП принимает максимальное значение. В граничной точке 0,4 ФП равна 0, так как ранее на основе субъективного суждения мы приняли, что при Р>0,4 вероятность не может быть малой.
| Граничные значения интервала | 0,0 | 0,4 |
| Значения ФП |
Графическая иллюстрация решения задачи показана на рисунке 10 а.
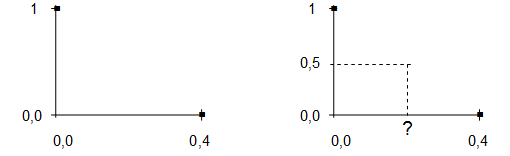
а) б)
Рисунок 10 – Значения ФП в граничных точках
Нахождение значений ФП в данном интервале.
Для этого можно использовать 3, 5, 7, 9 кратное разбиение интервала (следует помнить, что чем больше кратность разбиения, тем выше точность построения ФП).
Для простоты воспользуемся 3-х кратным разбиением. Методика разбиения состоит в следующем:
· назначьте значение аргумента, для которого значение ФП (0,5) лежит посередине между значениями ФП для точек 0,0 и 0,4.
Графическая иллюстрация постановки задачи приведена на рисунке 2 б.
Предположим, что это будет значение аргумента равное 0,35 (рисунок 3).
· назначьте значение аргумента, для которого значение ФП (0,25) лежит посередине между значениями ФП для точек 0,35 и 0,4.
Предположим, что это будет значение аргумента равное 0,38 (рисунок 11).
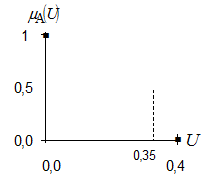
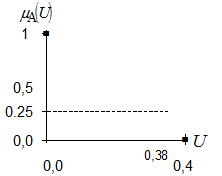
Рисунок 11 – Значения аргумента, Рисунок 12 – Значения аргумента,
Дата добавления: 2017-06-02; просмотров: 3162;
