При котором ФП принимает при котором ФП принимает
Значение 0,5 значение 0,25
· назначьте значение аргумента, для которого значение ФП (0,75) лежит посередине между значениями ФП для точек 0,0 и 0,35.
Предположим, что это будет значение аргумента равное 0,12 (рисунок 13).
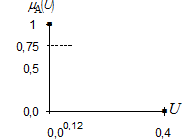
Рисунок 13 – Значения аргумента, при котором ФП принимает значение 0,75
Таким образом, результаты выполнения предыдущих действий для данного терма будут такими:
| Значения аргумента | 0,0 | 0,12 | 0,35 | 0,38 | 0,40 |
| Степени принадлежности | 1,0 | 0,75 | 0,50 | 0,25 | 0,0 |
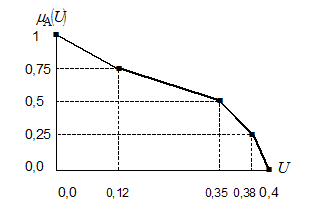
Рисунок 14 – Графическое изображение результатов
для терма "Вероятность малая"
7.2Рассмотрим 2 терм и определим семантику терма "Вероятность средняя". Для него определим значения ФП в граничных точках. В этом случае значения ФП равны 0, так как и меньше Р < 0,2 и при Р > 0,8 вероятность не может считаться средней.
Граничные значения 0,2 0,8
Значения ФП 0 0
Графически решение этой задачи показано на рисунке 15.
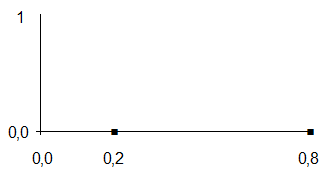
Рисунок 15 – Значения ФП в граничных точках
для терма "Вероятность средняя"
Нахождение значений ФП в данном интервале.
Для простоты воспользуемся 3-х кратным разбиением. Методика разбиения состоит в следующем:
· назначьте значение аргумента, при котором ФП уже равна 1, и значение аргумента, при котором она еще равна 1.
Предположим, это будут значения аргумента равные 0,3 и 0,7 (рисунок 16).

Рисунок 16 – Значения аргумента, при котором ФП принимает значение 1,0.
· назначьте значение аргумента, для которого значение ФП (0,5) лежит посередине между значениями ФП для точек 0,2 и 0,3.
Предположим, что это будет значение аргумента равное 0,27.
· назначьте значение аргумента, для которого значение ФП (0,75) лежит посередине между значениями ФП для точек 0,27 и 0,3.
Предположим, что это будет значение аргумента равное 0,282.
· назначьте значение аргумента, для которого значение ФП (0,25) лежит посередине между значениями ФП для точек 0,2 и 0,27.
Предположим, что это будет значение аргумента равное 0,24.
Рассмотрим правый полуинтервал для терма "Вероятность средняя".
· назначьте значение аргумента, для которого значение ФП (0,5) лежит посередине между значениями ФП для точек 0,7 и 0,8.
Предположим, что это будет значение аргумента равное 0,74.
· назначьте значение аргумента, для которого значение ФП (0,75) лежит посередине между значениями ФП для точек 0,7 и 0,74.
Предположим, что это будет значение аргумента равное 0,72.
· назначьте значение аргумента, для которого значение ФП (0,25) лежит посередине между значениями ФП для точек 0,74 и 0,8.
Предположим, что это будет значение аргумента равное 0,76.
Таким образом, результаты выполнения предыдущих действий для терма "Вероятность средняя" будут такими:
| Значения аргумента | 0,2 | 0,24 | 0,27 | 0,282 | 0,3 | 0,7 | 0,72 | 0,74 | 0,76 | 0,8 |
| Степени принадлежности | 0,0 | 0,250 | 0,500 | 0,750 | 1,0 | 1,0 | 0,75 | 0,5 | 0,25 |
Графически это решение показано на рисунке 17.

Рисунок 17 – Вид ФП для терма "Вероятность средняя"
7.3Рассмотрим 3 терм и определим семантику терма "Вероятность большая". Для него определим значения ФП в граничных точках.
| Граничные значения | 0,600 | 1,0 |
| Значения ФП |
Графически решение этой задачи показано на рисунке 18.
Нахождение значений ФП в данном интервале.
Методика выполнения данного этапа аналогична 7.1, поэтому представим только конечные результаты.
· значение аргумента, для которого значение ФП (0,5) лежит посередине между значениями ФП для точек 0,6 и 1,0 равно 0,7.
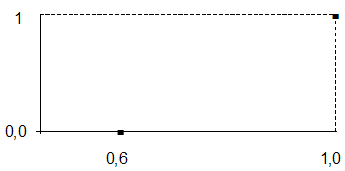
Рисунок 18 – Значения ФП в граничных точках
для терма "Вероятность большая"
· значение аргумента, для которого значение ФП (0,25) лежит посередине между значениями ФП для точек 0,6 и 0,7 равно 0,64.
· значение аргумента, для которого значение ФП (0,75) лежит посередине между значениями ФП для точек 0,7 и 1,0 равно 0,85.
Таким образом, результаты выполнения расчетов для данного терма будут такими:
| Значения аргумента | 0,6 | 0,64 | 0,7 | 0,85 | 1,0 |
| Степени принадлежности | 0,0 | 0,250 | 0,500 | 0,750 | 1,0 |
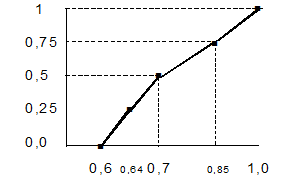
Рисунок 19 – Вид ФП для терма "Вероятность большая"
Вывод. Таким образом, в результате выполнения всех этапов можно построить функцию принадлежности лингвистической переменной "Вероятность" (рисунок 12).

Рисунок 20 – Общий вид функции принадлежности лингвистической
переменной "Вероятность"
КОСВЕННЫЙ МЕТОД ПОСТРОЕНИЯ ФП
Одним из возможных методов построения функции принадлежности является метод, основанный на количественном сравнении степеней принадлежности индивидуальным ЛПР (лицо, принимающее решение). Результатом опроса ЛПР является матрица 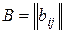 размера n´n, где n – число точек
размера n´n, где n – число точек  , в которых сравниваются значения функции принадлежности. Элемент
, в которых сравниваются значения функции принадлежности. Элемент 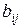 матрицы В является субъективной оценкой отношения
матрицы В является субъективной оценкой отношения 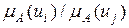 и показывает, во сколько раз, по мнению ЛПР,
и показывает, во сколько раз, по мнению ЛПР, 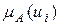 больше
больше  . Величина назначается в соответствии с балльной шкалой, значения которой интерпретируются в соответствии со шкалой интенсивности.
. Величина назначается в соответствии с балльной шкалой, значения которой интерпретируются в соответствии со шкалой интенсивности.
По определению 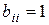 и с целью согласования оценок ЛПР устанавливается, что
и с целью согласования оценок ЛПР устанавливается, что 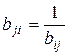 . Значения функции принадлежности
. Значения функции принадлежности 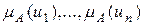 в точках
в точках  определяются на основе решения задачи о нахождении собственного вектора матрицы В
определяются на основе решения задачи о нахождении собственного вектора матрицы В
 ,
,
где 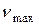 – максимальное собственное число матрицы В;
– максимальное собственное число матрицы В; 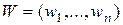 – соответствующий собственный вектор; т – символ транспонирования.
– соответствующий собственный вектор; т – символ транспонирования.
Поскольку матрица В является положительной по построению, решение этой задачи всегда существует и является единственным. Можно показать, что в этом случае
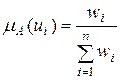 .
.
При этом значения функции принадлежности 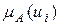 оказываются измеренными в шкале отношений. Описанный метод обладает рядом достоинств:
оказываются измеренными в шкале отношений. Описанный метод обладает рядом достоинств:
- применяемая в методе процедура парных сравнений является достаточно простой для ЛПР, поскольку она не навязывает ему априорных ограничений, например не требует транзитивности суждений;
- метод допускает наблюдаемую на практике несогласованность оценок эксперта (имеется в виду, что 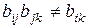 ) и вместе с тем позволяет учесть и оценить ее введением коэффициента несогласованности. Если
) и вместе с тем позволяет учесть и оценить ее введением коэффициента несогласованности. Если 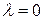 , то наблюдается ситуации полной согласованности суждений; чем больше l, тем больше несогласованность суждений ЛПР;
, то наблюдается ситуации полной согласованности суждений; чем больше l, тем больше несогласованность суждений ЛПР;
- решение задачи о собственном векторе приводит к измерению функции принадлежности в шкале отношений.
МОДЕЛЬНЫЙ ПРИМЕР
Для иллюстрации этапов получения решения задачи с помощью метода анализа иерархий рассмотрим гипотетический пример. Для уборки зерновых культур необходимо приобрести зерноуборочный комбайн. На рынке имеются машины нескольких фирм одинакового целевого назначения. Какой зернокомбайн выбрать в соответствии с потребностями покупателя? Другими словами необходимо оценить весомость критериев к машине, которыми пользуется потребитель.
Рекомендуется такая последовательность этапов при решении задачи.
1. Очертите проблему и определите, что вы хотите узнать.
2. Постройте иерархию, начиная с вершины (цели - с точки зрения управления), через промежуточные уровни (критерии, по которым зависят последующие уровни) к самому нижнему уровню (который обычно является перечнем альтернатив).
3. Постройте матрицу попарных сравнений для второго уровня.
4. Проверить согласованность, используя отклонение 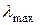 от n.
от n.
Схема иерархии для рассматриваемой задачи приведена на рисунке. На первом (высшем) уровне находится общая цель: "Зернокомбайн". На втором уровне находятся показатели (критерии), уточняющие цель.
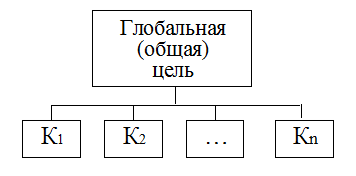
Рисунок 21 – Схема иерархии для решения проблемы выбора зернокомбайна
Примечание 1. В примере на втором уровне рассматриваются четыре критерия. Такое количество выбрано лишь для иллюстрации метода и не связано с сутью рассматриваемой проблемы – выбора лучшего зернокомбайна.
Примечание 2. Издавна известны магические свойства числа семь. Так вот в МАИ для проведения обоснованных численных сравнений не рекомендуется сравнивать более чем 7 ± 2 элементов. Если же возникает потребность в расширении уровней 2 и 3, то следует использовать принцип иерархической декомпозиции. Другими словами если число критериев, например, превышает десятки, то необходимо элементы сгруппировать в сравниваемые классы приблизительно из семи элементов в каждом.
После выполнения работ на этапе иерархического представления проблемы необходимо установить приоритеты критериев. Для количественного определения сравнительной важности факторов в проблемной ситуации необходимо составить матрицу попарных сравнений. Эта матрица представлена в таблице 1.
Таблица 1 – Общий вид матрицы попарных сравнений
| Общее удовлетворение машиной | A1 | A2 | A3 | . . . | AN |
| A1 | 1/1 | w1/w2 | w1/w3 | . . . | w1/wn |
| A2 | w2/w1 | 1/1 | w2/w3 | . . . | w2/wn |
| A3 | w3/w1 | w3/w2 | 1/1 | . . . | w3/wn |
| . . . | . . . | . . . | . . . | 1/1 | . . . |
| AN | wn/w1 | wn/w2 | wn/w3 | . . . | 1/1 |
Здесь A1, A2, A3, ..., An- множество из n элементов; w1, w2, w3, ..., wn- соответственно их веса или интенсивности.
Примечание 1. Цель составления подобной матрицы заключается в определении факторов с наибольшими величинами важности, чтобы затем сконцентрировать внимание на них при решении проблемы или разработке плана действий.
Примечание 2. Если ожидается, что w1, w2,..., wn – неизвестны заранее (а это очень распространенная ситуация), то попарные сравнения элементов производятся с использованием субъективных суждений, численно оцениваемых по шкале (см. приложение).
Примечание 3. Следует подчеркнуть, что в МАИ по соглашению сравнивается относительная важность левых элементов матрицы с элементами наверху. Поэтому если элемент слева важнее, чем элемент наверху, то в клетку заносится положительное целое (от 1 до 9); в противном случае – обратное число (дробь, например, 1/5). Относительная важность любого элемента, сравниваемого с самим собой, равна 1; поэтому диагональ матрицы (таблица 1) содержит только единицы. Наконец, обратными величинами заполняют симметричные клетки, т.е. если элемент А1 воспринимается как слегка более важный. (3 на шкале) относительно элемента А2, то считается, что элемент А2 слегка менее важен (1/3 по шкале) относительно элемента А1.
Составим матрицу попарных сравнений для нашей задачи (таблица 2).
Таблица 2 – Матрица попарных сравнений, построенная
на основе субъективных суждений
| Общее удовлетворение комбайном | Пр. | П.з. | Нар. | Р.т. | Ст. |
| Производительность | 1/1 | 5/1 | 4/1 | 5/1 | 3/1 |
| Потери зерна | 1/5 | 1/1 | 1/2 | 2/1 | 1/2 |
| Наработка | 1/4 | 2/1 | 1/1 | 1/1 | 1/4 |
| Расход топлива | 1/5 | 1/2 | 1/1 | 1/1 | 1/2 |
| Стоимость | 1/3 | 2/1 | 4/1 | 2/1 | 1/1 |
Синтез приоритетов
Одним из способов определения приоритетов является вычисление геометрического среднего. Это можно сделать, перемножая элементы в каждой строке и извлекая корень n-й степени, где n – число элементов. Полученный таким образом столбец чисел нормализуется делением каждого числа на сумму всех чисел. Последовательность расчета составляющих вектора приоритетов приведена в таблице 3.
Таблица 3 – Расчет вектора приоритетов
| А1 | А2 | А3 | А4 | Оценки компонент собственного вектора по строкам | Нормализация результата | |
| А1 | 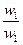
| 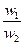
| 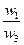
| 
| 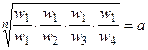
| 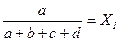
|
| А2 | 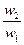
| 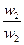
| 
| 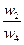
| 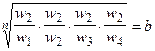
| 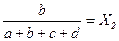
|
| А3 | 
| 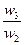
| 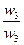
| 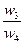
| 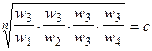
| 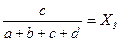
|
| А4 | 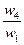
| 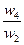
| 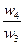
| 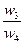
| 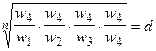
| 
|
Для нашего примера значения вектора приоритетов (функции принадлежности) приведены в таблице 4.
Таблица 4 – Функция принадлежности
| Общее удовлетворение комбайном | Вектор приоритетов, Xi |
| Производительность | 0,491 |
| Потери зерна | 0,099 |
| Наработка | 0,104 |
| Расход топлива | 0,086 |
| Стоимость | 0,220 |
Дата добавления: 2017-06-02; просмотров: 965;
