Построение функций принадлежности

Для использования в моделях принятия решений информации, формализованной на основе теории нечетких множеств, необходимы процедуры построения соответствующих функций принадлежности. Различные методы построения функций принадлежности нечетких множеств классифицируются по четырем аспектам:

1) предполагаемый вид области определения нечеткого множества: числовая – дискретная (а) или непрерывная (b) – и нечисловая (с);

2) применяемый способ экспертного опроса: индивидуальный (d₁), групповой (d₂);

3) тип используемой экспертной информации: порядковая (e₁), кардинальная (е₂);

4) интерпретация данных экспертного опроса: вероятностная (D), детерминированная (N).

Рассмотрим, например, процедуру 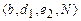построения функций принадлежности для термов лингвистической переменной с числовой областью определения на основе метода равноделения. ЛПР поочередно предъявляется несколько пар точек. При каждом предъявлении ЛПР должно назвать точку, для которой степень принадлежности находится посередине между степенями принадлежности точек, входящих в предъявленную пару.

На практике используется также процедура построения функций принадлежности, которая основана на их представлении в виде функций от плотности вероятности четких случайных границ между термами лингвистической переменной. Определять функции принадлежности можно не только с помощью процедур непосредственного опроса экспертов, но и на основе функций распределения F₁ и F₂ с дальнейшим использованием выражения, полученного для .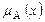

Сами функции F₁ и F₂ могут быть построены на основе либо статистических данных, либо экспертного опроса.

Для построения функции принадлежности используются: а) стандартный набор графиков; б) метод попарных сравнений; в) метод деления значений ФП пополам; г) метод равнокажущихся интервалов; д) метод последовательных интервалов; е) неизменная базовая переменная.