Выбор лучшей альтернативы в многокритериальной задаче с нечеткой исходной информацией
В том случае, когда имеется n критериев (j1, ..., jn), лучшим считается альтернативный вариант, удовлетворяющий сразу всем критериям. Тогда правило выбора наилучшей альтернативы может быть записано в виде пересечения соответствующих нечетких множеств
А = А1 Ç А2 Ç … Ç Аn.
Операции пересечения соответствует определение функции принадлежности альтернативы хj результирующему нечеткому множеству А альтернатив с идеальным значением интегрального критерия j как минимума из всех n значений функций принадлежности mАi(хj) альтернативы хj нечеткому множеству Аi альтернатив с идеальным значением свойства (критерия) ji:
mА(хj) = 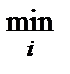 {mАi(хj)}.
{mАi(хj)}.
В качестве лучшей выбирается альтернатива хj, обеспечивающая наибольшее значение функции ее принадлежности mА(хj) результирующему нечеткому множеству А альтернатив с идеальным значением интегрального критерия j:
х* = arg 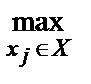 mА(хj) при хj Î X.
mА(хj) при хj Î X.
Пусть, например, указанные в предыдущем примере, 5 ЭВМ сравниваются по следующим критериям: j1 - производительность, j2 - надежность, j3 – стоимость. Данные критерии задают три нечетких множества:
А1 = {0,6/х1; 0,8/х2; 0,5/х3; 0,9/х4; 1,0/х5};
А2 = {0,7/х1; 0,7/х2; 0,6/х3; 0,8/х4; 0,4/х5};
А3 = {0,7/х1; 0,5/х2; 0,4/х3; 0,5/х4; 0,2/х5}.
Тогда правило выбора имеет вид;
А = {min {0,6; 0,7; 0,7}/х1; min {0,8; 0,7; 0,5}/х2; min {0,5; 0,6; 0,4}/х3; min {0,9; 0,8; 0,5}/х4; min {1,0; 0,4; 0,2}/х5} = {0,6/х1; 0,5/х2; 0,4/х3; 0,5/х4; 0,2/х5}.
Наилучшей альтернативой будет альтернатива х1, имеющая наибольшее значение функции принадлежности результирующему нечеткому множеству А альтернатив с идеальным значением интегрального критерия j: mА(х1) = 0,6.
Если критерии ji обладают разной важностью ki, то при задании функций принадлежности альтернатив нечетким множествам Аiki, на которых производится выбор, выполняются операции возведения в степень ki функций принадлежности альтернатив исходным нечетким множествам Аi. Решение задачи выбора сводится к определению
х* = arg  {
{ 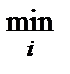 {mАiki (хj)}}.
{mАiki (хj)}}.
Сравнение альтернатив, свойства которых описываются числовыми лингвистическими переменными
В том случае, когда каждая из анализируемых альтернатив задается значениями некоторой лингвистической переменной, то для сравнения альтернатив необходимо произвести сравнение этих значений. В случае если используется числовая лингвистическая переменная, то необходимо произвести сравнение двух нечетких чисел [12], например, числа N (небольшое) и числа М (малое).
Рассмотрим случай, когда заданы функции принадлежности альтернатив двум нечетким множествам с двумя разными нечеткими идеальными значениями критерия j. Эти нечеткие идеальные значения критерия j оценивается нечеткими числами N и М соответственно.
На рисунке 5.4.2 приведен пример задания таких функций принадлежности, в котором базовая переменнаяR1 описывает значения емкости оперативной памяти ЭВМ. Эта переменная характеризует числовую лингвистическую переменную "емкость оперативной памяти", принимающую значения "малая величина", "небольшая величина".
Значение числовой лингвистической переменной "малая величина" описывается нечетким числом (нечетким множеством чисел) М, принимающим разные значения х в интервале [a; b]. mM(a)=0, mM(b)=0. Если a> х >b, то 0<mM(х)£1.
Значение числовой лингвистической переменной "небольшая величина" описывается нечетким числом (нечетким множеством чисел) N, принимающим разные значения у в интервале [g; d]. mN(g)=0, mN(d)=0. Если g>у>d, то 0<mN(у)£1.
Возможность того, что нечеткое число М больше или равно нечеткому числу N
V(М ³ N) = 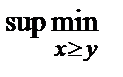 {mM(х), mN(у)},
{mM(х), mN(у)},
где sup определяет верхнюю грань возможности того, что значение х нечеткого числа М больше, чем значение у нечеткого числа N: х > у.
| N |
| M |
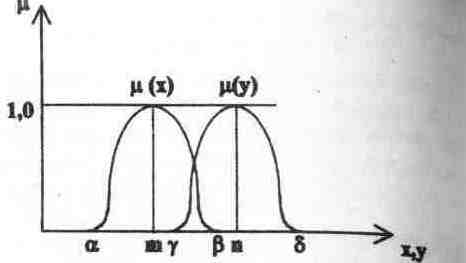
Рис. 5.4.2. Пример задания двух функций принадлежности
Рассмотрим пример, в котором функции принадлежности заданы треугольными формами. Нечеткое число (нечеткое множество чисел) М описывает значение лингвистической переменной "малая величина". Нечеткое число (нечеткое множество чисел) N - значение лингвистической переменной "небольшая величина". Данные треугольные формы пересекаются (рис. 3).
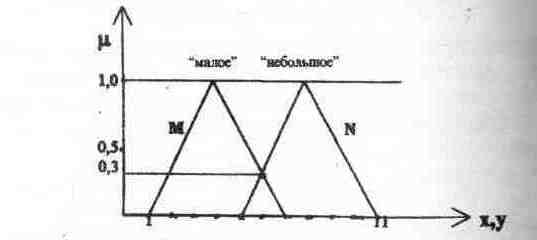
Рис. 5.4.3. Задание треугольных функций принадлежности чисел нечетким множествам чисел "малое число" и "небольшое число"
Согласно определению найдем V(М ³ N) = 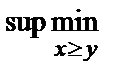 {mM(х), mN(у)}.
{mM(х), mN(у)}.
Возьмем различные пары значения х нечеткого числа М и значения у нечеткого числа N, таких что х ³ у:
х=2; у=0; min{mM(2), mN(0)}=0;
х=5; у=4; min{mM(5), mN(4)}=0;
х=6; у=6; min{mM(6), mN(6)}=0,3;
х=7; у=6; min{mM(7), mN(6)}=0.
Тогда возможность того, что нечеткое число М больше или равно нечеткому числу N
V(М ³ N) = 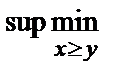 {0; 0; 0,3; 0}= 0,3.
{0; 0; 0,3; 0}= 0,3.
Найдем V(N ³ M) = 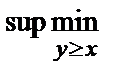 {mM(х), mN(у)}.
{mM(х), mN(у)}.
Возьмем различные пары значения х нечеткого числа М и значения у нечеткого числа N, таких что у ³ х:
х=2; у=3; min{mM(2), mN(3)}=0;
х=6; у=6; min{mM(6), mN(6)}=0,3;
х=4; у=6; min{mM(4), mN(6)}=0,3;
х=4; у=8; min{mM(4), mN(8)}=1,0;
х=4; у=11; min{mM(4), mN(11)}=0.
Тогда возможность того, что нечеткое число М больше или равно нечеткому числу N
V(N ³ M) = 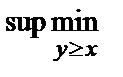 {0; 0,3; 0,3; 1,0; 0}= 1,0.
{0; 0,3; 0,3; 1,0; 0}= 1,0.
Следовательно, отношение М ³ N определяется бинарным нечетким множеством (т. е. множеством из двух элементов): А1={0,3/да; 1,0/нет}, а отношение N ³ M определяется бинарным нечетким множеством: А2={1,0/да; 0,3/нет}.
Пример линейного упорядочивания альтернатив, свойства которых и коэффициенты важности этих свойств заданы нечетко
Многокритериальная оценка и выбор альтернатив на основе нечетких множеств также базируется на приведенные в разделе 2.4 формы интегрального критерия [17]. Приведем решение задачи многокритериальной оценки для самой простой формы критерия при допущении о возможности треугольного представления функций принадлежности.
Пусть необходимо выполнить упорядочивание альтернатив, задаваемых вектором критериев, сворачиваемых в линейную форму.
Оценку j-й альтернативы по i-му критериюобозначим jij. Тогда линейная форма интегрального критерия, оценивающая j-ю альтернативу, будет иметь вид
jj = 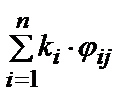 .
.
Рассмотрим пример, в котором значения оценок альтернатив по критериям jij и коэффициенты важности ki этих критериев задаются функциями принадлежности треугольной формы, т. е. ki и jij являются нечеткими числами, над которыми выполняются действия сложения и умножения. Результат этих операций представляет собой также нечеткое число (нечеткое множество чисел) А с функцией принадлежности альтернатив этому нечеткому множеству треугольной формы:
mА(z) = 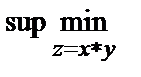 {mА(х), mА(у)},
{mА(х), mА(у)},
где * - знак, задающий операцию (сложения или умножения), z – это либо сумма двух нечетких чисел x и y, либо их произведение.
Так как функции принадлежности имеют вид треугольной формы, то они однозначно определяются тремя точками: левой границей, правой границей и точкой максимума mА. Поэтому для нахождения mА(z) достаточно выполнить три операции * с данными тремя точками
zL = хL * уL, zR = хR * уR, z. = х. * у.,
где индексы «L», «R», «.» указывают на эти три точки. В точках с индексами «L» и «R» значение функции принадлежности равно нулю, а в точке с индексом «.»значение функции принадлежности равно единице.
Пусть, например, нужно выбрать одну из двух альтернативных структур ЦВК, оцениваемых вектором j, который состоит из трех частных критериев:
Производительности – j1, надежности – j2, стоимости – j3.
Первый и второй частный критерии определены как важные, а третий – как очень важный. На рисунке 5.4.4 приведены функции принадлежности нормированных значений коэффициентов важности ki нечетким множествам, описывающим значения лингвистической переменной «важность критерия»: «не очень важный», «довольно важный», «важный», «очень важный».

Рис. 5.4.4. Функции принадлежности коэффициентов важности
В таблице 1 приведены оценки двух альтернативных вариантов структур ЦВК по критериям j1 – j3.
Таблица 1. Оценки альтернатив по критериям j1 – j3

На рисунке 5.4.5 приведены функции принадлежности нормированных значений оценок j-х альтернатив по i-м критериям jij нечетким множествам, описывающим значения лингвистической переменной «оценка по критерию»: «плохая», «удовлетворительная», «хорошая», «очень хорошая».
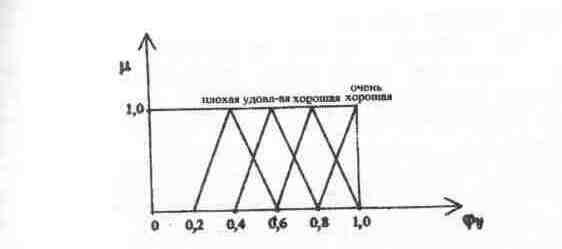
Рис. 5.4.5. Функции принадлежности оценок альтернатив по критериям
Воспользовавшись функциями принадлежностями, приведенными на рисунках 4 и 5, и правилами алгебраического умножения и алгебраического сложения нечетких множеств получим значения левой границы, правой границы и точки максимума треугольной функции принадлежности нечеткому числу j1 оценки первой альтернативы по интегральному критерию j:
j1L=j11L×k1L+j12L×k2L+j13L×k3L–j11L×k1L×j12L×k2L×j13L×k3L» »0,6×0,4+0,2×0,4+0,8×0,6–0,01=0,79;
j1R=j11R×k1R+j12L×k2R+j13R×k3R–j11R×k1R×j12L×k2R×j13R×k3R» »1,0×0,8+0,6×0,8+1,0×1,0–0,38=1,90;
j1.=j11.×k1.+j12.×k2.+j13.×k3.–j11.×k1.×j12.×k2.×j13.×k3.»
»0,8×0,6+0,4×0,6+1,0×0,8–0,9=1,43.
Аналогично определим значения подобных точек треугольной функции принадлежности нечеткому числу j2 оценки второй альтернативы по интегральному критерию j:
j2L=j21L×k1L+j22L×k2L+j23L×k3L–j21L×k1L×j22L×k2L×j23L×k3L» »0,6×0,4+0,6×0,4+0,4×0,6–0,1=0,71;
j2R=j21R×k1R+j22L×k2R+j23R×k3R–j21R×k1R×j22L×k2R×j23R×k3R» »1,0×0,8+1,0×0,8+0,8×1,0–0,51=1,89;
j2.=j21.×k1.+j22.×k2.+j23.×k3.–j21.×k1.×j22.×k2.×j23.×k3.»
»0,8×0,6+0,8×0,6+0,6×0,8–0, 1 = 1,33.
Полученные левые границы, правые границы и точки максимума функций принадлежности, которые определяют нечеткие числа j1 и j2, оценивающие качество соответственно первой и второй альтернативы, приведены на рисунке 5.4.6.
| m 1,0 0,92 j1 j2 0 0,71 0,79 1,33 1,43 1,9 j |
Рис. 5.4.6. Функции принадлежности альтернатив нечетким числам j1 и j2
Находя верхние из минимальных граней возможности того, что первая альтернатива лучше второй и наоборот, по аналогии с ранее рассмотренной однокритериальной оценкой, получим два бинарных нечетких множества А1 и А2, описывающих нечеткие отношения «первая альтернатива лучше второй» и «вторая альтернатива лучше первой».
Так бинарное нечеткое множество А1= {1,0/да; 0,92/нет}, а бинарное нечеткое множество А2= {0,92/да; 1,0/нет}. Из этих множеств видно, что лучшей является первая альтернатива, так как степень того, что первая альтернатива лучше второй, равна 1,0. Но степень того, что вторая альтернатива лучше первой, равна 0,92. Поэтому сравниваемые альтернативы имеют примерно одинаковое качество.
Принятие решения при нечетко заданном принципе оптимальности.
В ранее рассмотренных задачах принятия решений предполагалось, что нечетко задано множество оценок альтернатив W. Однако в задачах принятия решений возможна нечеткость и при задании принципа оптимальности (ПО).
Так, например, система предпочтений в функции СПО(W) может быть задана лицом, принимающим решение, в виде нечетких суждений. В этом случае используется понятие нечеткого высказывания, т.е. высказывания вида (х есть t), где х – наименование лингвистической переменной, t – нечеткая переменная, характеризующая ее значение. Правила преобразования высказываний, базирующиеся на логические операции объединения, пересечения, импликации и отрицания, позволяющие выполнить нечеткий вывод решения в виде нечеткого высказывания.
Таким образом, можно принять решение, пользуясь логическими правилами вида: "Если время на принятие решение мало и данные о воздушной цели, поступающие от различных источников, неполныили противоречивы, то желательно использовать режим децентрализованного управления средствами ПВО, иначе используется централизованное управление". Данное правило можно представить высказыванием вида
ЕСЛИ (х1 = t1) И ((х2 = t2)ИЛИ (х2 = t3))ТО (х3 = t4)ИНАЧЕ (х3 = t5).
Каждое нечеткое высказывание характеризуется нечетким множеством, задаваемым функцией принадлежности. Зная, как выполняются операции над нечеткими множествами, можно получить нечеткое решение, которое описывается нечетким множеством
РЕШЕНИЕ = {m А1ÇА2(z)/(х3 = t4); m А1ÇА2(z)/(х3 = t5)},
где mА1ÇА2(z) = min{mА1(х1), mА2(х2)}, в свою очередь mА2(х2) = mВ1ÈВ2(х2) = max{mВ1(х2), mВ2(х2)}.
mА1ÇА2(z) – функция принадлежности ситуации ПВО нечеткому множеству ситуаций, требующих управления средствами ПВО в децентрализованном режиме;
mА1(х1) – функция принадлежности времени на принятие решение нечеткому множеству «мало»;
mА2(х2) – функция принадлежности данных о воздушной цели нечеткому множеству «неполныили противоречивы»;
mВ1(х2) – функция принадлежности данных о воздушной цели нечеткому множеству «неполны»;
mВ2(х2) – функция принадлежности данных о воздушной цели нечеткому множеству «противоречивы».
Это нечеткое множество определяет предпочтительность выбора режима между децентрализованным и централизованным управлением средствами ПВО.
В предыдущем разделе указывалось, что последствия сделанного выбора могут быть неоднозначными. При этом данная неоднозначность может быть описана статистически или с помощью нечетких множеств. Для решения задач принятия решения втаких ситуациях необходима композиция методов математической статистики и теории нечетких множеств.
Дата добавления: 2018-06-28; просмотров: 1672;
