Числовые ряды с положительными членами. Достаточные признаки сходимости.
Определение 6.6. Если все 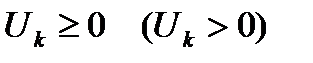 , то числовой ряд
, то числовой ряд 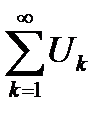 называется рядом с положительными членами (со строго положительными членами). Принято общий член таких рядов обозначать через
называется рядом с положительными членами (со строго положительными членами). Принято общий член таких рядов обозначать через 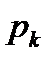 .
.
Теорема 6.6. Необходимое и достаточное условие сходимости ряда с положительными членами.
Для того, чтобы ряд с положительными членами 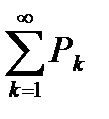 сходился, необходимо и достаточно, чтобы последовательность частичных сумм этого ряда
сходился, необходимо и достаточно, чтобы последовательность частичных сумм этого ряда 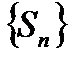 была ограничена.
была ограничена.
Доказательство:
а) Необходимость.
Пусть 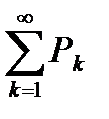 сходится. Тогда по определению последовательность частичных сумм этого ряда сходится, и, следовательно, по теореме Вейерштрасса она ограничена.
сходится. Тогда по определению последовательность частичных сумм этого ряда сходится, и, следовательно, по теореме Вейерштрасса она ограничена.
б) Достаточность.
Пусть 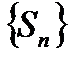 заданного ряда
заданного ряда 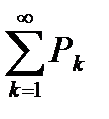 ограничена. Так как
ограничена. Так как 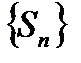 является неубывающей, то из ограниченности
является неубывающей, то из ограниченности 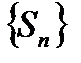 по теореме Вейерштрасса следует сходимость этой последовательности. Последнее, согласно определению, влечет за собой сходимость ряда
по теореме Вейерштрасса следует сходимость этой последовательности. Последнее, согласно определению, влечет за собой сходимость ряда 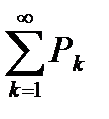 .
.
Теорема доказана.
Теперь перейдем к изучению некоторых достаточных признаков сходимости рядов с положительными членами.
Теорема 6.7. Первый признак сравнения.
Если имеем два ряда с положительными членами 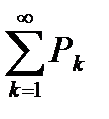 и
и 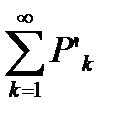
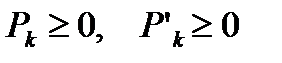 и для всех к удовлетворяется неравенство
и для всех к удовлетворяется неравенство 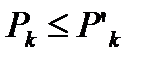 , то из сходимости ряда
, то из сходимости ряда 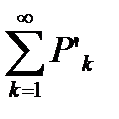 следует сходимость ряда
следует сходимость ряда 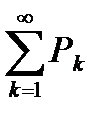 , а из расходимости ряда
, а из расходимости ряда 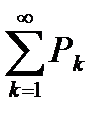 следуетрасходимость ряда
следуетрасходимость ряда 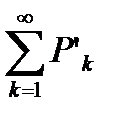 .
.
Дата добавления: 2018-11-25; просмотров: 650;
