Методы обработки экспертной информации
Так, метод непосредственной оценки предполагает сопоставление каждому альтернативному варианту xi одного числа аik. Результирующая оценка, позволяющая упорядочить варианты, получается суммированием таких оценок с учетом весов экспертов:
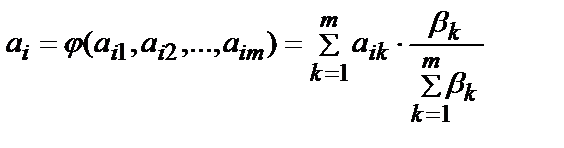 ,
,
где bk – вес каждого эксперта;
m – количество экспертов.
Шкала оценок может быть либо только положительной, например, в диапазоне от 0 до 100 или от 0 до 10, либо включать положительные и отрицательные числа. В этом случае положительные значения соответствуют улучшению оцениваемого свойства, а отрицательные – его ухудшению.
При отсутствии информации о компетенции экспертов полагают bk=1. Тогда 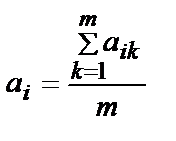 .
.
В том случае, если вместо численных оценок используются ранги, т. е. вместо шкал интервалов используются шкалы порядков, в ходе экспертного опроса применяют методы ранжирования.
Методы ранжирования используются в тех случаях, когда при сравнении альтернатив по некоторым свойствам не требуется производить точные измерения соответствующих параметров или данное измерение в настоящее время не может быть произведено по причинам практического или теоретического характера.
Каждый эксперт ранжирует оцениваемые альтернативы. При ранжировании он должен их расположить в порядке, который представляется ему наиболее рациональным, и присвоить каждой альтернативе число натурального ряда – ранг. При этом ранг 1 получает наиболее предпочтительная альтернатива, а ранг n – наименее предпочтительная.
Все оцениваемые альтернативы упорядочиваются в соответствии с величиной
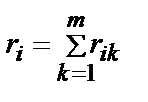 ,
,
где rik- рангi-й альтернативы, присваиваемый k-м экспертом.
В том случае, если эксперт не может определить отношение строгого порядка между альтернативами, используется нестрогое ранжирование. При этом производится упорядочивание альтернатив. Тем альтернативам, для которых отношения строгого порядка определить не удалось, присваивается стандартизированный ранг, значение которого представляет среднее сумму мест установленного порядка, поделенных между собой объектами с одинаковыми рангами.
Пусть, например, пяти альтернативам присвоены ранги:
| Номер альтернативы | |||||
| Ранги |
Тогда альтернативам х3 и x4 присваивается стандартизированный ранг (2+3)/2=2,5.
Альтернативы х2 и x5 оцениваются стандартизированным рангом (4+5)/2=4,5.
Результат стандартизированного нестрогого ранжирования имеет следующий вид:
| Номер альтернативы | |||||
| Ранги | 4,5 | 2,5 | 2,5 | 4,5 |
Суммирование рангов и численных оценок приводит к процедуре получения общей оценки а. Дефектом такой процедуры является то, что небольшое значение одной частной оценки может быть компенсировано большим значением другой оценки, а также то, что не учитывается значимость отдельных параметров.
Для учета связей между отдельными параметрами может быть использован метод последовательных предпочтений. В данном методе принимается допущение об аддитивности результатов отдельных оценок (о возможности складывать оценки).
Суть процедуры, реализующей метод, заключается в следующем. Эксперту предоставляется перечень альтернатив, которые необходимо оценить по их относительной важности и произвести их ранжирование. Наиболее важной альтернативе присваивается вес 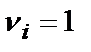 . Остальным альтернативам интуитивно присваиваются веса
. Остальным альтернативам интуитивно присваиваются веса 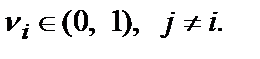
Затем эксперт устанавливает, являетсяли альтернатива с оценкой веса 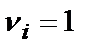 важнее, чем сумма всех остальных альтернатив.
важнее, чем сумма всех остальных альтернатив.
Затем он сравнивает 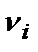 с
с 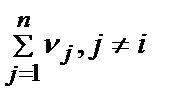 и корректирует значениявесов
и корректирует значениявесов 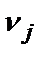 .
.
Далее определяется вторая наиболее важная по значимости альтернатива с весом 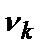 . Важность этой альтернативы сравнивается с важностью всех оставшихся n – 2 альтернатив и т.д.
. Важность этой альтернативы сравнивается с важностью всех оставшихся n – 2 альтернатив и т.д.
Затем он сравнивает 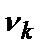 с
с 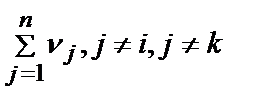 и корректирует значениявесов
и корректирует значениявесов 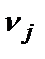 .
.
Рассмотрим приведенный ранее пример ранжирования показателей х1 – х7.
В результате опроса экспертов выявлено, что наиболее важной является альтернатива х5.
Проанализировав результаты ранжировки, присвоим 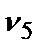 =1;
=1; 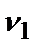 =0,5;
=0,5; 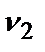 =0,4;
=0,4; 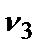 =0,8;
=0,8; 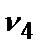 =0,4;
=0,4; 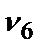 =0,7;
=0,7; 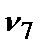 =0,6.
=0,6.
Допустим, мы определили, что параметр х5 менеезначим, чемвсе другие параметры (альтернативы). Этому соответствует неравенство 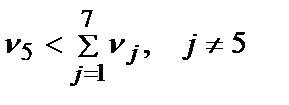 . Выберем следующую по важности альтернативу
. Выберем следующую по важности альтернативу 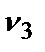 =0,8. Определим, что параметр х3 менее значим, чем сумма всех другихальтернатив:
=0,8. Определим, что параметр х3 менее значим, чем сумма всех другихальтернатив: 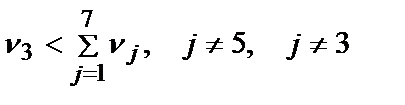 .
.
Следующий по важности параметр х6; 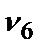 =0,7. Пусть параметр х6 важнее, чем сумма оставшихся параметров. Однако
=0,7. Пусть параметр х6 важнее, чем сумма оставшихся параметров. Однако 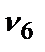 <
< 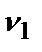 +
+ 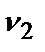 +
+ 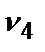 +
+ 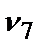 . Откорректируем значения этих весов. Получим
. Откорректируем значения этих весов. Получим 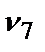 =0,3,
=0,3, 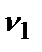 =0,2;
=0,2; 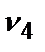 =0,1;
=0,1; 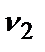 =0,05.
=0,05.
В дальнейшем наиболее важной является альтернатива х7, которая (допустим) важнее оставшихся трех альтернатив. Откорректируем их веса. Получим 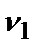 =0,15;
=0,15; 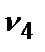 =0,08;
=0,08; 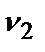 =0,05.
=0,05.
Больше значения весов изменять не будем.
В результате таких последовательных шагов корректуры весов получим их итоговые оценки. Их сумма равна 3,08.
Произведем нормирование этих весов, путем деления значения 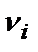 на 3,08. В результате получим итоговые значения экспертизы (обработки мнений экспертов с целью упорядочивания альтернатив), которые определяют линейный порядок альтернатив и показывают насколько одна альтернатива предпочтительней другой:
на 3,08. В результате получим итоговые значения экспертизы (обработки мнений экспертов с целью упорядочивания альтернатив), которые определяют линейный порядок альтернатив и показывают насколько одна альтернатива предпочтительней другой:
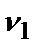 =0,05;
=0,05; 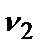 =0,02;
=0,02; 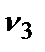 =0,26;
=0,26; 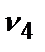 =0,03;
=0,03; 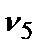 =0,32;
=0,32; 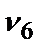 =0,23;
=0,23; 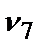 =0,1.
=0,1.
Заметим, что при использовании данного метода исследователь должен вести постоянный диалог с экспертами, выясняя: важнее ли анализируемая альтернатива, чем все еще не проанализированные альтернативы.
Рассмотренный метод становится громоздким при большом числе сравниваемых альтернатив в связи с тем, что каждая альтернатива одновременно сравнивается со всеми другими альтернативами. Кроме того, большую трудность для экспертов представляет одновременный учет нескольких признаков, по которым необходимо сравнивать альтернативы
Для сокращения размерности задачи экспертного оценивания целесообразно использовать метод парных сравнений.
В данном методе k-й эксперт сравнивает каждую альтернативу с каждой. Результатом такого сравнения является матрица Аk размерности n´n, в которой
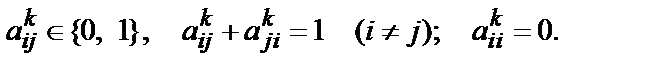
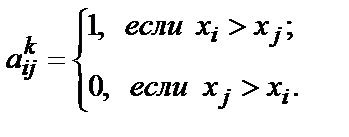
После экспертного опроса получают m матриц Аk, каждая из которых выражает мнение одного k-го эксперта.
Для получения общей оценки используют процедуру суммирования. Причем сначала вычисляют матрицу 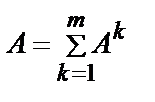 .
.
Затем находят итоговую оценку каждойi-й альтернативы 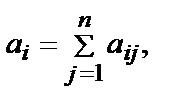
где 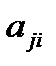 – элемент матрицы А.
– элемент матрицы А.
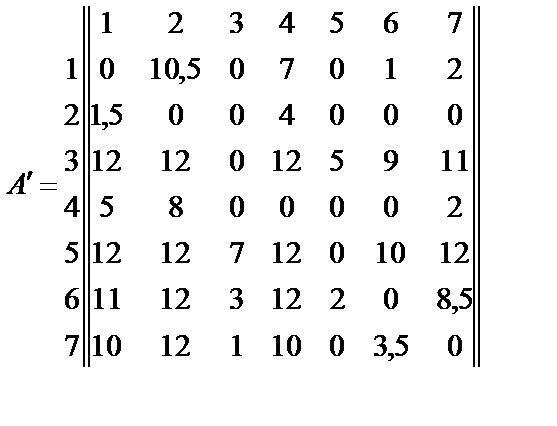
Для рассмотренного примера определения важностипоказателей х1 – х7, используемых при выборе корабельной ЭВМполучаем матрицу А, заполненную без учета величин ½ для пар альтернатив (вместо ½ в матрице стоит 0), получивших у эксперта оценку эквивалентности (равенства), и матрицу 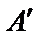 , заполненную с учетом величин ½ для пар альтернатив, получивших у эксперта оценку эквивалентности (равенства)
, заполненную с учетом величин ½ для пар альтернатив, получивших у эксперта оценку эквивалентности (равенства)
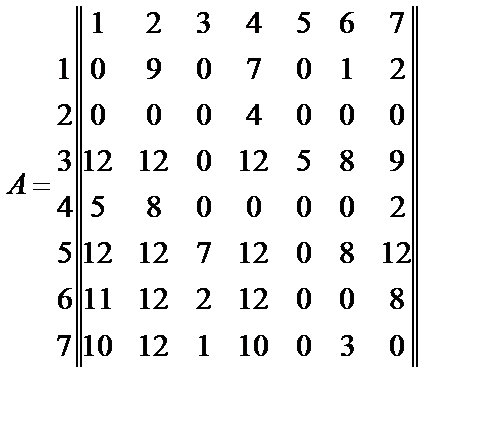
Найдем итоговую оценку для каждой альтернативы матрицы А: а1=19; а2=4; а3=58; а4=15; а5=63; а6=45; а7=36;
Найдем итоговую оценку для каждой альтернативы матрицы 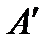 : а1=20,5; а2=5,5; а3=61; а4=15; а5=65; а6=48,5; а7=36,5;
: а1=20,5; а2=5,5; а3=61; а4=15; а5=65; а6=48,5; а7=36,5;
Таким образом, наиболее значимым для выбора ЭВМ является значение параметра наработки на отказ, наименее значимым - емкости памяти на сменных носителях (при любом из двух способов заполнения итоговой матрицы).
Дата добавления: 2018-06-28; просмотров: 787;
