Теория статистических решений
Многоэтапные алгоритмы процессов принятия управленческих решений в условиях неопределенности, когда решения зависят от исхода предыдущих решений, графически могут быть представлены в виде «дерева» решений. Ситуации, в которых задается последовательность принятия решений игроками (их может быть 2, 3 и т.д.), описываются с помощью «позиционных игр». Здесь «игроки» принимают решения, зная о всех предыдущих решениях партнеров. Такие игры могут быть представлены в виде «дерева» решений. «Дерево» решений – это графо-аналитическая модель, позволяющая наглядно представить логическую структуру принятия решений.
Составляя дерево решений, рисуют «ветви» (дуги графа), отображающие структуру проблемы. Располагают дерево решений слева направо. Ветви обозначают возможные альтернативные варианты управленческого решения и возможные исходы в результате реализации этих решений.
Квадраты на «дереве» решений обозначают «узлы», в которых принимаются решения, круги – «узлы» исходов, вероятностных событий. Влиять на появление тех или иных исходов не представляется возможным (в таких узлах возникающих неопределенностей дальнейшее развитие процесса зависит от влияния внешних условий), но для каждой ветви, исходящей из круглых «узлов», определяют вероятности проявления соответствующих исходов. После построения дерева (включающего все решения и исходы), каждый из вариантов решений и исходов анализируется и на модели – «дереве» проставляются соответствующие доходы. Все расходы, вызванные решениями, проставляются на соответствующих ветвях. Анализ «дерева» решений производится в обратном порядке (справа налево). Для каждого узла неопределенности рассчитывается математическое ожидание результата (прибыли). Для каждого пункта принятия решений ожидаемый результат максимизируется. Лучшее решение выбирается по максимуму результата реализации решения.
Задача. Партию товара, затраты на которую составили 200 ден.ед., фирма планирует продать с прибылью. Однако существует риск, что слишком высокая продажная цена замедлит, а то и вовсе остановит реализацию товара, и фирма вместо прибыли получит одни убытки. По мнению экспертов фирмы, вероятность продажи товара по цене выше 400 ден. ед. вообще равна нулю.
В то же время снижение продажной цены ради ускорения процесса реализации тоже должно иметь какие-то разумные пределы. Продажа данной партии товара, например по цене ниже 200 ден. ед., приносит фирме прямые убытки.
Определить оптимальный уровень продажной цены за данную партию товара на предстоящих торгах.
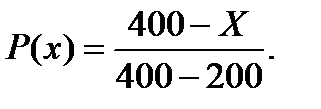 Решение. Поскольку продавать данный товар по цене ниже 200 ден. ед. не выгодно, а по цене выше 400 ден. ед. невозможно, определим вероятность продажи всей партии товара по цене Х в интервале 200-400 ден. ед. Это можно сделать по формуле
Решение. Поскольку продавать данный товар по цене ниже 200 ден. ед. не выгодно, а по цене выше 400 ден. ед. невозможно, определим вероятность продажи всей партии товара по цене Х в интервале 200-400 ден. ед. Это можно сделать по формуле
Вероятность же того, что вся партия может оказаться непроданной, найдем как Q(x) = 1 – P(x).
Величины P(x) и Q(x) можно трактовать не только как вероятности, но и как доли проданной и непроданной продукции.
Возможную прибыль от реализации всей партии по цене Х определим как Х – 200.
Проделав с помощью приведенных формул соответствующие расчеты, получим следующую таблицу.
| Запрашиваемая цена (х) | Вероятность того, что партия будет | Размер прибыли, ден. ед. | |
| продана Р(х) | не продана Q(х) | ||
| 0,75 | 0,25 | ||
| 0,5 | 0,5 | ||
| 0,25 | 0,75 | ||
На основе этих данных построим дерево решений и с его помощью найдем оптимальное решение, касающееся уровня запрашиваемой цены на предстоящих торгах.
Дерево решений изображено на рис. 7.1. Пункт принятия решений на нем обозначен квадратом. Из него выходят пять дуг (ветвей), соответствующих пяти вариантам запрашиваемой цены: 200, 250 и т. д. На концах выходящих из квадратной вершины ветвей стоят круглые вершины, изображающие узлы возникновения неопределенностей (поскольку, приняв то или иное решение, мы еще не знаем, что оно нам даст).
Из каждого узла неопределенности выходят по две ветви, соответствующие двум возможным исходам: товар будет продан (П) и товар не будет продан (Н). Возле каждой ветви проставляются соответствующие вероятности. На самых концах финальных ветвей проставляется ожидаемая прибыль или убытки от того, что партия товара будет продана или не будет.
| 1 0 0 -50 0,75 50 0,25 -50 0,5 100 0,5 -50 0,25 150 0,75 -50 0 200 1 -50 |
| 0 0 |
| -50 |
Рис. 7.1. Дерево решений по определению цены продажи
Величину убытков для всех вариантов решений примем условно на уровне 25 % от затрат, допустив, что товар обесценится на четверть, если не будет продан на ближайших торгах. В каждой реальной ситуации их находят, сообразуясь с конкретными обстоятельствами.
После построения дерева решений начинается его обратный анализ. Идя по ветвям дерева справа налево и попадая в круглые вершины, проставим рядом с ними математические ожидания прибыли, которая рассчитывается следующим образом:
М(х1) = 0 * 1 – 50 * 0 = 0,
М(х2) = 50 * 0,75 – 50 * 0,25 = 25,
М(х3) = 100 * 0,5 – 50 * 0,5 = 25,
М(х4) = 150 * 0,25 – 50 * 0,75 = 0,
М(х5) = 200 * 0 – 50 * 1 = -50.
Двигаясь далее влево, дойдем до квадратной вершины – узла принятия решения, рядом с которым проставим максимальную величину из тех, что стоят на концах выходящих из него ветвей. В нашей задаче таких величин две (обе равны 25) и они соответствуют решениям о назначении цены продаж на уровне 250 и 300.
Для принятия окончательного решения необходимо проверить, нет ли между двумя наибольшими значениями результатов третьего, с еще большим значением прибыли. Сделаем проверку для цены в 275 ден. ед.:
Р(275) = (400-275)/(400-200) = 0,625 , Q(275) = 1-0,625 = 0,375 ,
прибыль составит 275 – 200 = 75, убытки равны 50.
Отсюда М(275) = 75 * 0,625 – 50 * 0,375 = 28,125.
Таким образом, приняв решение о цене продажи в 275 ден. ед., можно обеспечить более высокий результат, чем при ценах в 250 или 300 ден. ед.
Для уточнения сделаем еще одну проверку в окрестностях цены, равной 275 ден. ед., и найдем, что отклонения от нее как в большую, так и в меньшую сторону снижают ожидаемую прибыль. Так, для цен в 270 и 280 ден. ед. прибыль получится равной 28 ден. ед.
Значит, окончательное оптимальное решение – остановиться на цене в 275 ден. ед.
Возможно построение с самого начала более подробной модели дерева решений с более мелким шагом изменения цены продаж, например в 25 или 5 ден. ед. Тогда оптимальное решение было бы получено сразу, без дополнительных проверок. Однако в таком случае само дерево оказалось бы более громоздким, что дало бы менее экономичный путь нахождения оптимального решения. Поэтому целесообразнее строить дерево с более крупным шагом, а потом провести проверку в нужном месте с более мелкой градацией цены продаж.
Задача. Допустим необходимо выбрать лучший из трех инвестиционных проектов: ИП1, ИП2, ИП3, которые требуют вложения средств в размерах 200, 300 и 500 ден. ед. и могут дать прибыль в размере 100, 200 или 300 ден. ед. соответственно.
Риск потери этих средств по проектам характеризуется на уровне 10; 5 и 20 %. Определить, какой проект даст большее значение прибыли.
| -200 |
| -300 |
| -500 |
| 0,9 |
| 0,95 |
| 0,05 |
| 0,8 |
| 0,2 |
| 0,1 |
Рис. 7.2. Дерево решений по выбору инвестиционного проекта
Определим соответствующие математические ожидания прибыли по проектам:
М(х1) = 100 * 0,9 – 200 * 0,1 = 70,
М(х2) = 200 * 0,95 – 300 * 0,05 = 175,
М(х3) = 300 * 0,8 – 500 * 0,2 = 140.
Наибольшее математическое ожидание прибыли, равное 175 ден. ед., соответствует принятию решения о реализации второго проекта.
Дата добавления: 2018-06-28; просмотров: 818;
