Понятие нечеткого множества
Если неопределенность ситуации определена на расплывчатой шкале, то лицо, принимающее решение, имеет дело с задачами принятия решений при нечеткой ситуации. Понятие нечеткости формализуется с помощью теории нечетких множеств. Нечеткое множество образуется путем введения обобщенного понятия принадлежности элемента множеству.
Если в четких множествах переход от принадлежности элемента х четкому множеству Х (х Î Х) к его непринадлежности этому четкому множеству (х Ï Х) происходит скачком, то в нечетком множестве такой переход происходит плавно, постепенно. Причем степень данного перехода может быть выражена числом в диапазоне [0, 1]. Таким образом, нечетким множествомА называется совокупность упорядоченных пар вида [17]:
А = {m(х)/х)},
где m(х)Î[0, 1] – степень принадлежности элемента нечеткому множеству А.
Если m(х) = 0, то элемент х определенно не принадлежит множеству А. Если m(х) = 1, то он определенно входит в данное множество. Характерным для нечеткого множества является такая ситуация, что хотя бы для одного элемента х m(х) ¹ 0 и m(х) ¹ 1. В противном случае будем иметь дело с четким, полностью определенным множеством.
Нечеткость – это такое свойство объектов и явлений, при котором не выполняется отношение эквивалентности: объект (явление) может одновременно принадлежать некоторому классу и не принадлежать ему. Функция принадлежности указывает, с какой степенью уверенности анализируемый объект принадлежит указанному классу. При этом он одновременно с различными степенями уверенности может принадлежать к различным классам.
Теория нечетких множеств позволяет формально описать лингвистические переменные.
Оценка нечетких свойств альтернатив при помощи лингвистических переменных
Лингвистической называется переменная, значениями которой являются слова или предложения естественного языка. Более строго понятие лингвистической переменной определяется пятеркой [12]
L = <X, Т, U, G,М>,
где Х – имя лингвистической переменной;
Т – множество значений лингвистической переменной {t}, представляющих собой нечеткие переменные t;
U – множество значений базовой переменной {u};
G – синтаксическая процедура, описывающая процесс образования новых значений лингвистической переменной – новых нечетких переменных;
М – семантическая переменная, позволяющая приписывать каждому новому значению лингвистической переменной – новой нечеткой переменной t, образованной с помощью процедуры G, некоторую семантику (смысловое значение).
Нечеткой переменной t называется двойка t= <xt, At>, где
xt – имя нечеткой переменной;
At = {m(u)/u} – нечеткое множество, описывающее возможные значения нечеткой переменной t (т. е. значения базовой переменной uÎ U) и степень принадлежности каждого из них m(u) нечеткому множеству At.
Так, например, понятие "вооружение надводного военного корабля" описывается лингвистической переменной L = <"вооружение надводного военного корабля", {сильное, слабое}, {МПК, МРК, ЭМ УРО, БПК, РКР, ТАРКР, ТАВКР}, G, М >.
Понятие "разрешающая способность графического адаптера Персональной ЭВМ" описывается лингвистической переменной L = <"разрешающая способность графического адаптера", {малая, большая} {МСGА, СGА, ЕGА, VGА, SVGА}, G, М>, где G - синтаксическая процедура (грамматика), позволяющая оперировать элементами множества Т (малая, большая), логическими операциями и модификаторами вида «И, ИЛИ, ОЧЕНЬ, НЕ, СЛЕГКА» для образования новых значений лингвистической переменой (т. е. нечетких переменных t); М – процедура экспертного опроса, в результате которой каждой вновь образованной нечеткой переменной t присваивается смысловое значение (семантику).
В частности, возможно получение новых значений лингвистической переменой "разрешающая способность графического адаптера Персональной ЭВМ": " малая ИЛИ большая", "НЕ большая", "ОЧЕНЬ большая" и др.
Самостоятельно приведите возможные новые значения лингвистической переменой "вооружение надводного военного корабля".
Для задания лингвистической переменной каждому ее значению ставятся в соответствие нечеткие множества. Так, например, лингвистическая переменная "быстродействие процессора INTEL" описывается двумя значениями лингвистической переменной: "процессор со средним быстродействием" и "процессор с высоким быстродействием", которым соответствуют нечеткие множества А1 и А2:
А1={0,1/80386; 0,2/80486; 0,4/Pentium; 0,7/Pentium-2; 0,9/Pentium-3; 0,6/Pentium-4};
А2={0,0/80386; 0,0/80486; 0,1/Pentium; 0,2/Pentium-2; 0,4/Pentium-3; 0,9/Pentium-4}.
В приведенных примерах множество U является не числовым, а перечислимым (дискретным). Если множество UÎR1 (т. е. состоит из числовых значений базовой переменной), то лингвистическая переменная называется числовой лингвистической переменной.
Основные виды функций принадлежности альтернатив нечеткому множеству
Поскольку m(х) является исчерпывающей характеристикой нечеткого множества, то оно может быть полностью задано функцией m = m(х) и представлено графиком этой функции.
Аппроксимация результатов научных описаний позволяет выделить основные виды функции принадлежности, приведенных на рисунке 5.4.1.
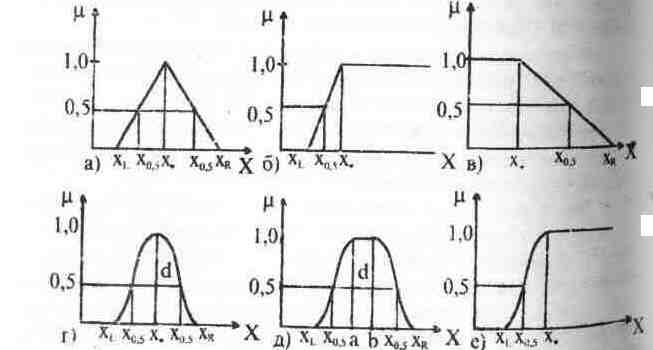
Рис. 5.4.1. Основные виды функции принадлежности
Функция принадлежности, приведенная на рисунке 5.4.1а, называется треугольной (Т - функцией). Данная функция может быть задана абсциссами трех точек, соответствующих левой границе треугольника (XL), правой границе треугольника (XR), а также вершине треугольника (X.).
Функции, приведенные на рисунках 5.4.1б, 5.4.1в, являются частными случаями Т - функции, в которой XL или XR стремятся бесконечности. Форма таких функций называется S – формой.
На рисунках 5.4.1г – 5.4.1е приведены p - функции, задаваемые (X.), а также (XL) и (XR) или (X0,5 – значениями x, при которых функция принадлежности равна 0,5) и формой зависимости, определяющей кривизну функции. Так, например, может быть использована зависимость для задания функции принадлежности вида рисунке 5.4.1д:
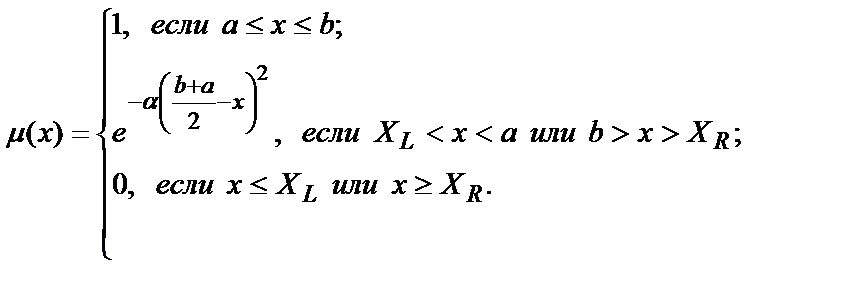
Дата добавления: 2018-06-28; просмотров: 944;
