С использованием распределения Стьюдента
Степень согласованности мнений экспертов при численных оценках (полученных, например, методом непосредственной оценки) определяется с помощью дисперсииs 2или оценки дисперсии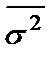 ;
;
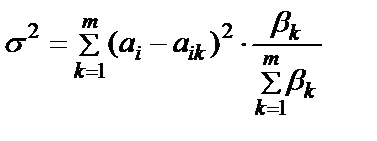 или
или 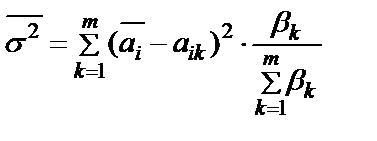 ,
,
где ai – математическое ожидание оценки альтернативы по i-му критерию m экспертами,
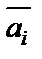 – среднее арифметическое оценок альтернативы по i-му критерию m экспертами.
– среднее арифметическое оценок альтернативы по i-му критерию m экспертами.
Если веса экспертов не установлены:
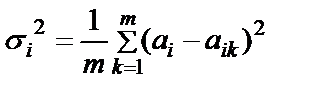 .
.
Задавшись уровнем значимостиai, можно определить границы интервала, в котором будет находиться результирующая оценка а:
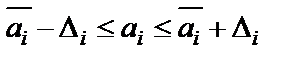 , где
, где 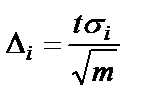 .
.
Величина t имеет распределение Стьюдента с m – 1 степенями свободы.
Если относительный (нормализованный) коэффициент согласованности мнений экспертов больше 0,1, т. е. интервал, в котором находится оцениваемая величина, является большим, то данный факт говорит о том, что мнения экспертов недостаточно согласованы. Для повышения согласованности оценок необходим дополнительный сеанс экспертизы.
Оценка согласия экспертов при использовании методов ранжирования с помощью коэффициента конкордации (согласия) W.
Для процедуры строгого ранжирования 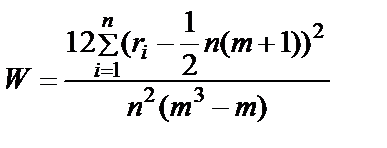 .
.
Для процедуры нестрогого ранжирования
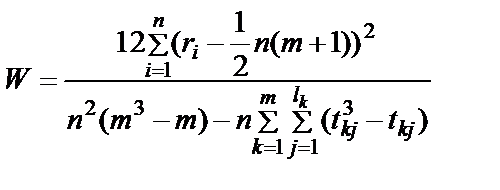 ,
,
где 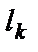 – число групп равных рангов, введенных k–м экспертом;
– число групп равных рангов, введенных k–м экспертом;
tkj – количество дробных рангов в j–й ( 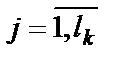 ) группе, введенных k–м экспертом;
) группе, введенных k–м экспертом;
ri – сумма рангов, присвоенных i–й альтернативе;
m – количество экспертов;
n – количество сравниваемых альтернатив.
Статистическую значимость ранжировки проверяют следующим образом. Выбирают значение a. Вычисляют величину 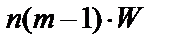 . Из таблиц распределения c2 для числа степеней (m–1) находят табличное значение величины
. Из таблиц распределения c2 для числа степеней (m–1) находят табличное значение величины 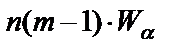 . В том случае, если полученное значение
. В том случае, если полученное значение 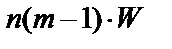 больше табличного, полученная ранжировка статистически значима. В противном случае необходимо организовать дополнительный сеанс экспертизы.
больше табличного, полученная ранжировка статистически значима. В противном случае необходимо организовать дополнительный сеанс экспертизы.
Оценим статистическую значимость ранжировки из таблицы 1. Эта ранжировка является нестрогой. Она содержит группы равных рангов у всех экспертов кроме восьмого, десятого и двенадцатого:
m = 12, n =7;
r1=63,5, r2=78,5, r3=23, r4=69, r5=19, r6=35,5, r7=47,5,
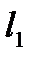 =1,
=1, 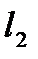 =1,
=1, 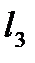 =2,
=2, 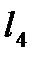 =1,
=1, 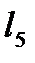 =1,
=1, 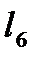 =1,
=1, 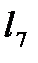 =1,
=1, 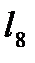 =0,
=0, 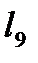 =1,
=1, 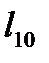 =0,
=0, 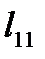 =1,
=1, 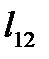 =0;
=0;
t11=2, t21=2, t31=2, t32=2, t41=2, t51=2, t61=2, t71=2, t91=2, t11.1=2.
W = 0,47; 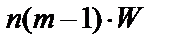 = 7×11×0,47 = 36,19.
= 7×11×0,47 = 36,19.
Для значения a = 0,05 и числа степеней свободы 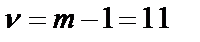 из таблиц распределения c2 получаем c20,05(11) = 19,675, что соответствует табличному значению величины
из таблиц распределения c2 получаем c20,05(11) = 19,675, что соответствует табличному значению величины 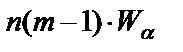 . Так как
. Так как 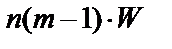 = 36,19 >
= 36,19 > 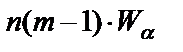 = 19,675, то полученная ранжировка является статистически значимой.
= 19,675, то полученная ранжировка является статистически значимой.
Дата добавления: 2018-06-28; просмотров: 455;
