Непрерывность функции
Опр.: Функция 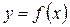 называется непрерывной в точке х0, если она определена в некоторой окрестности этой точки и
называется непрерывной в точке х0, если она определена в некоторой окрестности этой точки и 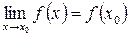
 |
Функция называется непрерывной слева (справа) в точке 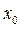 , если она определена в некоторой окрестности слева (справа) от точки
, если она определена в некоторой окрестности слева (справа) от точки 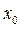 и
и
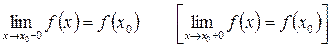
Опр.: Функция называется непрерывной в интервале, если она непрерывна в каждой точке этого интервала.
Опр.: Точки, в которых, функция не является непрерывной называются точками разрыва.
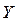
 Классификация точек разрыва
Классификация точек разрыва
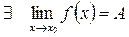
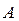


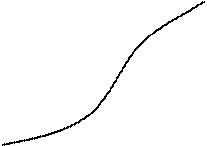 1.
1.
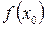

 Если
Если
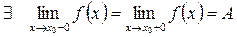 |
т.е.
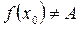 |
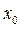
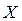
 но
но
(если в точке 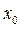 функция не определена)
функция не определена)
то 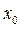 – точка устранимого разрыва I-го разряда.
– точка устранимого разрыва I-го разряда.
Пример:
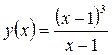 при
при 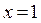 функция неопределенна.
функция неопределенна.
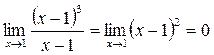
т.о. 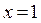 – точка устраняемого разрыва 1-го рода.
– точка устраняемого разрыва 1-го рода.
Доопределив функцию в токе 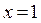 , получим:
, получим:
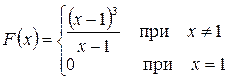
Новая функция будет уже непрерывна в точке 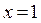 .
.
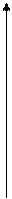 2.
2.
 | ||||||||
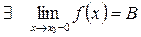 | ||||||||
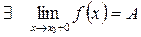 | ||||||||
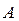 | ||||||||
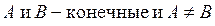 | 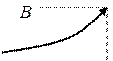 | |||||||
то 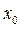 – точка конечного разрыва I-го рода.
– точка конечного разрыва I-го рода. 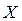
Опр.: Скачком функции в точке разрыва I-го рода называется величина:
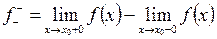
Пример:
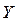

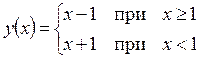
 при
при 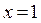
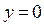


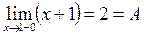
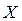
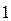

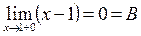
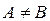 в точке
в точке 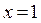 разрыв I рода.
разрыв I рода.
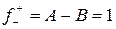
3.Все остальные – точки разрыва II рода.
 | 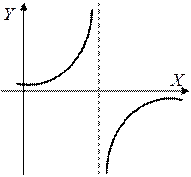 | 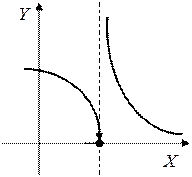 | |||
Пример:
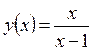 при
при 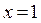 функция неопределенна
функция неопределенна
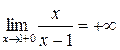
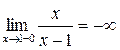
Т.к. односторонние пределы (достаточно было бы одного) бесконечны, то 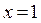 – точка разрыва II-го рода.
– точка разрыва II-го рода.
Примеры вычисления замечательных приделов:
1. 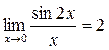 т.к.
т.к. 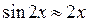
2. 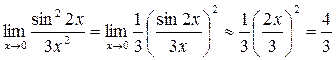
3. 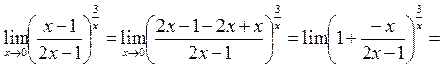
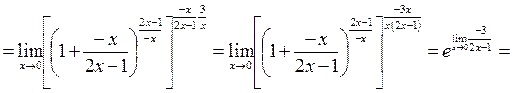
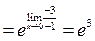
т.к. 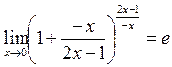 при
при 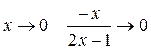
Дата добавления: 2017-09-19; просмотров: 509;
