Лекция 3. ПРОИЗВОДНЫЕ И ИХ ВЫЧИСЛЕНИЕ
Вопросы:
1. Понятие производной, ее геометрический и физический смысл.
2. Правила дифференцирования.
3. Производные высших порядков. Дифференциал функции.
1. Понятие производной 
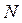


 Пусть М – некоторая точка кривой γ
Пусть М – некоторая точка кривой γ
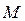 Если
Если 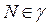 и
и 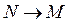 , то
, то
секущая 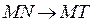 , если она
, если она

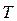 существует. Предельное положение
существует. Предельное положение
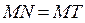 – касательная к γ в точке М.
– касательная к γ в точке М.
Пусть 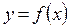 определена в некоторой точке х и ее окрестности. Дадим аргументы х приращение
определена в некоторой точке х и ее окрестности. Дадим аргументы х приращение 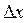 , при этом
, при этом 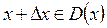 . Тогда функция получит приращение
. Тогда функция получит приращение 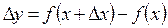 .
.
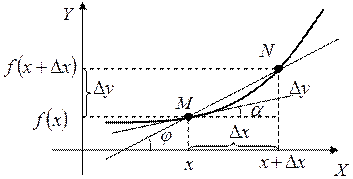 |
Опр.: Производной функции 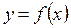 в точке х называется предел отношения приращения функции к приращению аргумента при стремлении к нулю, если это предел существует.
в точке х называется предел отношения приращения функции к приращению аргумента при стремлении к нулю, если это предел существует.
Обозначения 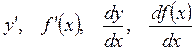
Итак, по определению
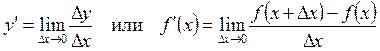 (*)
(*)
Процесс нахождения производной называется дифференцированием этой функции.
Функция называется дифференцируемой в некоторой точке х, если существует предел см. (*).
Непрерывность есть необходимое (но не достаточное) условие дифференцируемости функции.
Функция непрерывная в некоторой точке х может быть и не дифференцируемой в этой точке.
Пример: 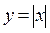 в точке х = 0 не дифференцируема.
в точке х = 0 не дифференцируема.
Дата добавления: 2017-09-19; просмотров: 439;
