Лекция 2. ТЕОРИЯ ПРЕДЕЛОВ.

1. Предел числовой последовательности.

2. Предел функции в бесконечности и в точке.

3. Замечательные пределы.

4. Непрерывность функции Основные теоремы о пределах

Предел числовой последовательности

Опр.: Если по некоторому закону каждому натуральному числу n поставлено в соответствие число a_n, то говорят, что задана числовая последовательность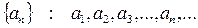

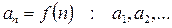– элементы числовой последовательности.

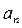– общий член или n-ый член.

Рассмотрим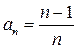

Опр.: Число А называется пределом числовой последовательности 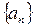, если 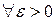найдется такой номер N (зависящий от 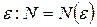, что для всех элементов последовательности с номерами n > N верно неравенство: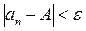

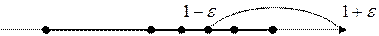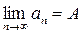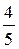
0 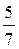1

Геометрический смысл: Число A – есть 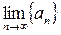, если 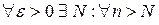все члены 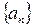будут заключены в ε-окрестность точки А, какой бы узкой она не была. Вне этой окрестности – только конечное число членов .

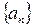Опр.: Последовательность называется сходящейся если существует конечный предел этой последовательности, в противном случае последовательность называется расходящейся.