Уравнение прямой на плоскости
1. Уравнение прямой с угловым коэффициентом
 |
 Пусть прямая пересекает ось Оy в т.ч. В(0; b) и образует с осью Оx угол
Пусть прямая пересекает ось Оy в т.ч. В(0; b) и образует с осью Оx угол
α (0 < α < 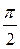 )
)
Возьмем произвольную точку М (x; y) принадлежащую прямой
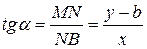
введем уголовной коэффициент
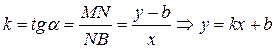 (1)
(1)
Частные случаи:
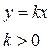
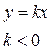
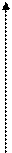 1)
1) 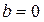 2)
2) 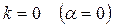 3)
3) 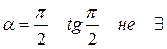
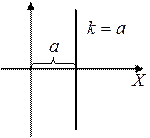 | |||||
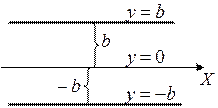 | |||||
 | |||||
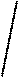 2. Уравнение прямой, проходящей через данную точку в данном направле-
2. Уравнение прямой, проходящей через данную точку в данном направле-
нии
Пусть прямая проходит через точку 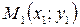 и образует с осью Ох угол
и образует с осью Ох угол 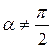
Т.к. 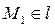 , то ее координаты удовлетворяют уравнению (1), т.е.
, то ее координаты удовлетворяют уравнению (1), т.е.
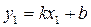
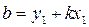 Подставим значение в (1)
Подставим значение в (1)
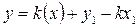
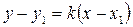 (2)
(2)
Уравнение (2) с различными значениями k называют так же уравнением пучка прямых с центром в точке 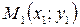 .
.
Из этого пучка нельзя определить лишь прямую, параллельную оси Оy.
3. Уравнение прямой, проходящей через две точки
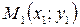
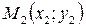 ,
,
если прямая проходит через 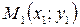
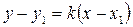
М2 тоже принадлежит этой прямой, следовательно 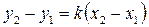
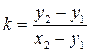
подставим k в уравнение (2):
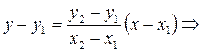
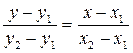 (4)
(4)
если 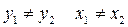 .
.
Если 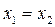 , то прямая параллельна Оy
, то прямая параллельна Оy
Если 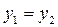 , то прямая параллельна Оx
, то прямая параллельна Оx
4. Уравнение прямой в отрезках
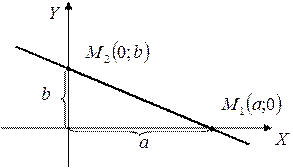 |
Прямая пересекает ось Ох в точке 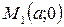 ; Оy в точке
; Оy в точке 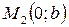 , т.е отсекает на осях координат отрезки длиной a и b.
, т.е отсекает на осях координат отрезки длиной a и b.
Используя уравнение (4) для точек 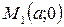 и
и 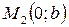 :
:
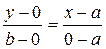
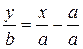
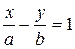 (5)
(5)
5. Общее уравнение прямой:
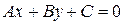
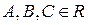 , причем
, причем 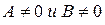 одновременно.
одновременно.
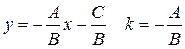
Некоторые частные случаи!
1) 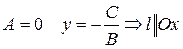
2) 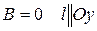
3) 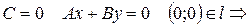 прямая проходит через начало координат
прямая проходит через начало координат
6. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
l проходит через 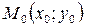
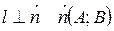
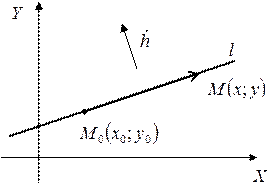 |
Возьмем 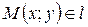 и
и 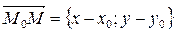 , т.к.
, т.к. 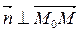 то их скалярное произведение равно 0, т.е.
то их скалярное произведение равно 0, т.е. 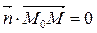
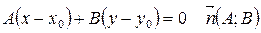 – нормаль (7)
– нормаль (7)
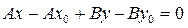
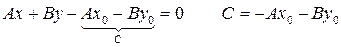 , тогда
, тогда
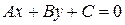 – общее уравнение прямой, где А и В – координаты вектора нормали
– общее уравнение прямой, где А и В – координаты вектора нормали 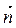
Дата добавления: 2017-09-19; просмотров: 550;
