Множества и операции над ними

ФУНКЦИОНАЛЬНАЯ ВЗАИМОСВЯЗЬ

Вопросы:

1. Множества и операции над ними.

2. Понятие функции.

3. Уравнение прямой и взаимное расположение прямых на плоскости.

4. Уравнение плоскости.

5. Взаимное расположение прямой и плоскости в пространстве.

6. Кривые второго порядка.

Множества и операции над ними

Опр.: Множество – совокупность объектов, которые рассматриваются как единое целое.

Объекты, которые образуют множество называются элементами или точками этого множества.

Пример:

1) Множество студентов группы.

2) Множество предприятий страны.

3) Множество R.

Обозначение: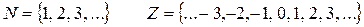

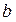
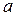
Если

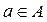
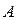
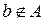
Опр.: Множество, не содержащее ни одного элемента называется пустым и обозначается Ø.

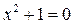
Множество действительных корней Ø.

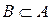
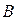
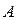
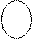B является подмножеством А,

если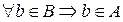

Опр.: Два множества А и В называются равными, если они состоят из одних и тех же элементов.

.

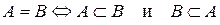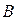
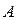Операции над множествами:

1. Объединение

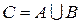
каждый элемент 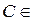хотя бы

одному из множеств А или В.

 

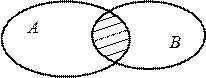
2. Пересечением 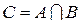каждый элемент 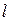принадлежащий и множеству А, и множеству В.

 

 

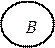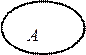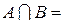Ø

 

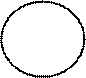
3. Разностью двух множеств А и В

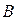
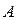
называется С = А \ В,

каждый элемент 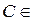множеству А,

но .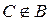

 

Пример:

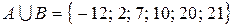
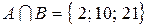
А \ В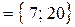

А \ В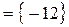

Понятие функции

Понятие функции является центральным для всей математики.

Опр.: Постоянной величиной называется величина сохраняющая одно и то же значение (π = 3,14…, е = 2,7182…).

Если величина сохраняет постоянное значение лишь в условиях данного процесса, то она называется параметром.

Опр.: Переменной называется величина, которая может принимать различные числовые значения.

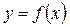Опр.: Если каждому элементу множества X 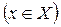ставится в соответствие единственный элемент y множества Y 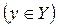, то говорят, что на множестве X задана, функция .

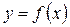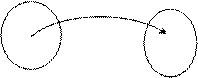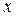
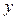
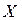
X – область определения

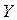Y – область значения.

x – называется независимой переменной (аргументом)

y – зависимая переменная

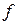– обозначает знак соответствия

Опр.: Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий (+, –, : , *) n операций сложной функции, называется элементарными.

Опр.: Пусть функция 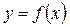определена на множестве U с областью значений Y, а переменная U является функцией 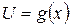, определенной на множестве X с областью значений U. Тогда заданная на множестве функция 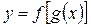называется сложной функцией или композицией функций .

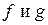Обратная функция

Опр.: Пусть 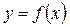: 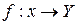. Поставим в соответствие каждому 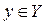единственное значение 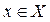, при котором 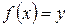, тогда функция 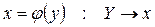называется обратной.

Вопросы:

1. Уравнение прямой и взаимное расположение прямых на плоскости.

2. Уравнение плоскости.