Эффективная диверсификация со многими рискованными активами
Первое, что должен сделать инвестор, желающий использовать теорию Е — V (теория Марковица), это придать количественный смысл своим предположениям относительно ожидаемых доходностей и дисперсий доходностей рассматриваемых ценных бумаг на определенном временном горизонте (периоде удержания). Эти параметры можно получить эмпирически. Инвестор может рассмотреть прошлую историю ценных бумаг и рассчитать доходности и их дисперсии за определенные периоды. Для определения ожидаемой доходности в период удержания можно использовать линейную регрессию по прошлым доходностям. Дисперсия как входной параметр определяется путем расчета дисперсии каждой прошлой точки данных на основе ее спрогнозированного значения (а не на основе линии регрессии, рассчитанной для прогнозирования следующей ожидаемой доходности). Вместо того чтобы определять эти значения эмпирическим способом, инвестор может оценить значения будущих доходностей и дисперсий. Возможно, наилучшим способом нахождения параметров является комбинация обоих подходов. Инвестору следует использовать эмпирический подход (т.е. использовать исторические данные), затем, если это необходимо, можно учесть прогноз относительно будущих значений ожидаемых доходностей и дисперсий.
Рисунок 10.10 показывает множество вариантов возможных портфелей. Если у вас портфель P3, то лучше заменить его на портфель P1, где прибыль такая же, но с меньшим риском, или на портфель P2, где вы получите большую прибыль при том же риске.
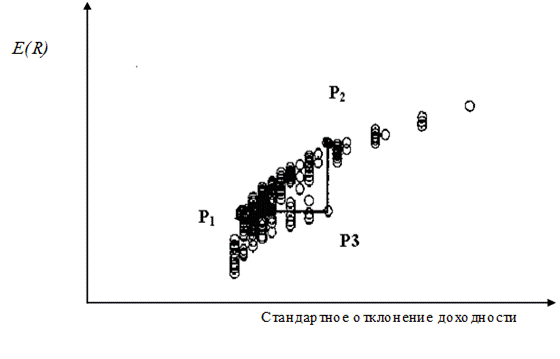
Рис.10.10. Современная теория портфеля.
Цель современной теории портфеля заключается в формировании самых «северо-западных» портфелей с точки зрения ожидаемой доходности и стандартного отклонения всей возможной совокупности ценных бумаг.
Следующими параметрами, которые должен знать инвестор для использования данного метода, являются коэффициенты линейной корреляции доходностей. Эти параметры можно получить эмпирически, путем оценки или с помощью комбинации обоих подходов.
При определении коэффициентов корреляции важно использовать точки данных того же временного периода, который был использован для определения ожидаемых доходностей и дисперсий.
Описывая эту ситуацию, Марковиц ввел понятие «эффективная граница» (efficient frontier). Это набор портфелей, которые находятся в верхней левой части графика, то есть портфели, прибыль которых больше не может быть увеличена без увеличения риска, и риск которых не может быть уменьшен без уменьшения прибыли. Портфели, находящиеся на эффективной границе, называются эффективными портфелями (см. рисунок 10.11).
Портфели, которые находятся вверху справа и внизу слева, в целом недостаточно диверсифицированы по сравнению с другими портфелями. Те же портфели, которые находятся в середине эффективной границы, обычно очень хорошо диверсифицированы. Выбор портфеля инвестором зависит от степени неприятия риска инвестором – иначе говоря, от желания взять на себя риск. В модели Марковица любой портфель, который находится на эффективной границе, является хорошим выбором, но какой именно портфель выберет инвестор – это вопрос личного предпочтения.
Модель Марковица первоначально была представлена для портфеля акций, который инвестор будет держать достаточно долго. Поэтому основными входными данными были ожидаемые доходы по акциям (определяется как ожидаемый прирост цены акции плюс дивиденды), ожидаемые дисперсии этих доходов и корреляции доходов между различными акциями.
Для того, чтобы представить, каким образом дополнительные рискованные активы могут улучшить инвестиционные возможности инвестора, рассмотрим рис.10.11. Точками А, В, С обозначены ожидаемая доходность и дисперсия для трех акций.
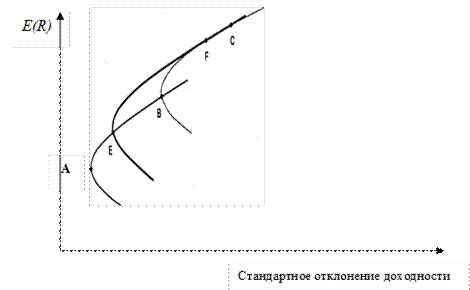
Рис.10.11. Формирование инвестиционных портфелей.
Дополнительные рискованные активы могут улучшить инвестиционные возможности инвестора. Кривая EF представляющая собой инвестиционные возможности портфеля состоящего из трех рискованных активов, смещена к «северо-западу», т.е. в желаемом для инвестора
направлении.
А, В и С обозначены ожидаемая доходность и стандартное отклонение для трех активов. Кривая, проходящая через точки А и В, показывает все возможные для них комбинации "риск-доходность". Аналогично, кривая, которая проходит через точки В к С, показывает все портфели, получаемые объединением этих активов. Сейчас посмотрим на точку Е на кривой АВ и точку F на кривой ВС. Эти точки представляют собой два возможных портфеля из комбинаций активов, представленных кривыми АВ и ВС. В свою очередь, кривая, проходящая через точки Е и F, представляет все портфели, которые могут быть получены путем объединения портфелей Е и F. И поскольку портфели E и F сами созданы из активов А, В и С, то такая кривая может рассматриваться как такая, которая описывает портфели рискованных активов, сформированные из трех бумаг. Отметим, что кривая EF смещает множество инвестиционных возможностей к северо-западу, т.е. в желаемом для инвестора направлении. Далее мы можем продолжить отбор других точек, представляющих портфели активов, лежащих на этих трех кривых, и комбинировать их в новые портфели, сдвигая подобным образом множество возможностей дальше на северо-запад. Можно увидеть, что чем больше акций, тем лучших результатов можно достичь. Более того, эффективная граница, обрамляющая все созданные нами подобным образом кривые, будет лежать в стороне (к северо-западу) от расположения индивидуальных бумаг (рис. 10.12).
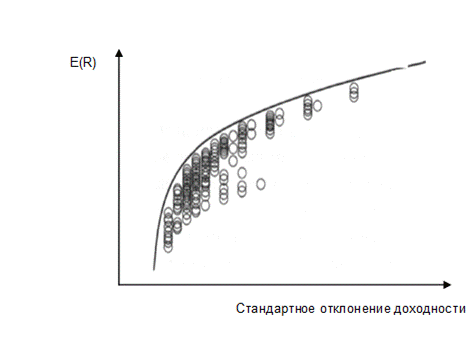
Рис.10.12. Эффективная граница как огибающая множества рискованных портфелей.
Кривая, соединяющая все самые «северо-западные» портфели, называется границей эффективного множества портфелей (эффективная граница) рискованных активов.
Эффективная граница – это кривая, представляющая совокупность портфелей рискованных активов, которая максимизирует ожидаемые ставки доходности при каждом уровне риска портфеля. Сочетания «ожидаемая доходность – стандартное отклонение» для любого отдельно взятого актива замкнуты внутри эффективной границы рискованных активов, поскольку портфели с отдельным активом неэффективны по определению (они не являются эффективно диверсифицированными).
Эта ситуация может быть представлена в матричном виде на примере портфеля из трех активов.
Допустим мы имеем 3 бумаги А, В, С с ожидаемыми нормами доходности RA,RB,RC и следующей матрицей ковариаций:
А В С
А 146 187 145
В 187 854 104
С 145 104 289
Значение дисперсий и ковариаций:
Var(RA)=146, Var(RB)=854, Var(RC)=289, Cov(RA,RB)=187, Cov(RA,RC)=145, Cov(RB,RC)=104.
Допустим ваш портфель имеет следующие пропорции: 0,5 бумаг А; 0,3 – В и 0,2 – С (заметьте их сумма составляет 1).
Доходность портфеля: RP = 0,5RA+0,3RB+0,2RC .
Можно найти дисперсию портфеля из следующей матрицы:
0,5 0,3 0,2
0,5 146 187 145
0,3 187 854 104
0,2 145 104 289
Затем берем каждую ячейку ковариационной матрицы умножаем на колонку и строчку пропорций и получаем:
36,6 28,05 14,5
28,05 76,86 6,24
14,5 6,24 11,56
Затем для получения дисперсии портфеля мы суммируем все строки результирующей матрицы:
Var(RP)= 36,5+28,05+14,5+ 28,05+76,86+6,24+14,5+6,24+11,56 = 201,76.
Волатильность (Vol) это квадратный корень из вариации = 14,204.
Дисперсия портфеля (Var(RP)), состоящего из «n» активов, рассчитывается по формуле:
Var(RP) = 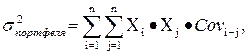 (10.11)
(10.11)
где Covi-j – ковариация доходности активов, входящих в портфель;
Xi, Xj – удельные веса активов в общей стоимости портфеля.
Знак двойной суммы в этой формуле означает, что при вычислениях дисперсии сначала для расчета величины Xi, Xj Covi-j удельный вес первого актива Xi умножается на произведение Xj Covi-j для всех видов активов, затем берется удельный вес второго актива и умножается на то же произведение для всех активов, начиная с первого. Указанные произведения суммируются, и таким образом находится значение дисперсии по совокупности активов, входящих в портфель.
Для дисперсии портфеля состоящего из «n» активов можно записать ковариационную матрицу размером «n × n = n2» следующим образом:
| … | n | ||||
| x12σ12 | x1x2σ12 | x1x3σ3n | … | x1xnσ1n | |
| x2x1σ21 | x22σ22 | x2x3σ3n | … | x2xnσ2n | |
| x3x1σ31 | x3x2σ32 | x32σ32 | … | x3xnσ3n | |
| … | … | … | … | … | … |
| N | xnx1σn1 | xnx2σn2 | xnx3σn3 | … | xn2σn2 |
Поскольку ковариация актива с самим собой является дисперсией, то на главной диагонали расположены дисперсии различных активов. Количество диагональных элементов всегда такое же, как количество бумаг в портфеле. Количество недиагональных элементов возрастает гораздо быстрее, чем количество диагональных. Так как дисперсия портфеля равна сумме всех элементов матрицы, то можно сделать общий вывод: дисперсия портфеля, состоящего из множества ценных бумаг, больше зависит от ковариаций между отдельными ценными бумагами, нежели от дисперсий отдельных ценных бумаг. При стремлении количества ценных бумаг к бесконечности, дисперсии отдельных ценных бумаг полностью элиминируются, однако ковариации остаются. Таким образом здесь проявляется эффект диверсификации. Дисперсии отдельных ценных бумаг устраняются путем диверсификации, а ковариация – нет.
Вернемся к иллюстрации инвестиционного риска в главе 9 на рис. 9.2.(см. рис. 10.13) и продемонстрируем риск портфеля инвестора. Инвестиционный риск определяется в портфельной теории дисперсией доходности портфеля. График демонстрирует, что дисперсия портфеля состоящего только из одной ценной бумаги, равна var (дисперсии самой этой ценной бумаги). Дисперсия портфеля снижается по мере того, как увеличивается количество ценных бумаг, что является доказательством эффекта диверсификации. Однако дисперсия портфеля никогда не может снизиться до нуля – пределом ее снижения является ковариация между каждой парой ценных бумаг (cov).

Рис. 10.13. Зависимость дисперсии портфеля от количества ценных бумаг.
Общий риск (var) – это риск, которому подвергается инвестор, владея только одной ценной бумагой. Портфельный риск – это риск, который остается после достижения полной диверсификации (cov). Диверсифицируемый риск – это риск, который может быть элиминирован в большом портфеле.(var-cov).
Риск, принимаемый инвестором, может быть выражен следующим образом:
Общий риск Портфельный риск Несистематический риск
отдельной = (cov) + (var-cov)
ценной бумаги
(var)
Ценовая модель рынка капитала (модель оценки финансовых активов) (САРМ)
Краеугольным камнем современной финансовой теории является модель оценки финансовых активов или ценовая модель рынка капитала, которую чаще всего обозначают аббревиатурой САРМ (Capital Asset Pricing Model). Автором модели является У.Ф.Шарп, который использовал метод составления портфеля Марковица, но упростил процедуру поиска эффективного портфеля. Для этого Шарп ввел так называемый β – фактор, который играет особую роль в ценовой модели рынка капитала.
САРМ позволяет точно прогнозировать взаимосвязь между риском какого-либо финансового актива и его ожидаемой доходностью. Эта зависимость выполняет две жизненно важные функции.
Во-первых, она позволяет получить эталонную ставку доходности, т.е. ее «объективное» значение в соответствии с присущим уровнем риска ценной бумаги, которой можно воспользоваться для оценки предполагаемых инвестиций. Во-вторых, эта модель помогает делать обоснованные предположения относительно ожидаемой доходности активов, которыми еще не торговали на рынке, например, при установлении цены акций первоначально поступивших в открытую продажу. Модель дает ответ на вопрос о том, какими должны были бы быть премии за риск, на которые согласны инвесторы в ситуации рыночного равновесия, если бы все они руководствовались одними и теми же прогнозами относительно ожидаемых ставок доходностей и рисков инвестиций в ценные бумаги, делая при этом оптимальный выбор для своих портфелей ценных бумаг в соответствии с принципами эффективной диверсификации.
Несмотря на то, что САРМ не совсем выдерживает проверку практикой, это не мешает ее повсеместному распространению, что объясняется углубленным пониманием сути описываемых процессов, которое обеспечивает эта модель, а также тем, что точности этой модели вполне достаточно для многих важных приложений.
Основополагающий принцип теории рынка капитала заключается в том, что равновесные рыночные цены должны исключать возможность арбитража. Если фактические цены финансовых активов допускают возможность арбитража, появляющиеся в результате этого возможности для прибыльной торговли ценными бумагами порождают сильное давление на цены активов, которое будет сохраняться до момента восстановления равновесия. Для заключения огромного объема торговых сделок лишь небольшому числу инвесторов достаточно знать о возможности арбитража, и их действия снова установят равновесие на рынке. Поэтому рыночные силы, которые препятствуют арбитражу, чрезвычайно мощные. Первыми исследовали эти противодействующие силы на финансовом рынке Модильяни (Modiliani) и Миллер (Miller) — Нобелевские лауреаты (за 1985 и 1990 годы).
Базовая версия САРМ предполагает ряд упрощающих допущений и ее главная идея заключается в том, что инвесторы ведут себя максимально похоже. Различия инвесторов заключаются в начальном уровне богатства, а также в их склонности к риску. Основные положения модели:
1. Все инвесторы предпочитают рыночный портфель – это портфель, в котором доля каждой ценной бумаги пропорциональна ее доли в общей капитализации рынка.
2. Рыночный портфель располагается на эффективной границе. Более того, в точке касания графика распределения капитала (CAL, см. рис.9.3) с эффективной границей он будет оптимальным рискованным портфелем. На рисунке 10.14 представлен график рынка капитала (CML – Capital Market Line), т.е. линия, проходящая от точки безрисковой ставки доходности к точке рыночного портфеля M, которая является наилучшим из возможных графиков распределения капитала.
Поскольку каждый инвестор использует рыночный портфель в качестве оптимального рискованного портфеля, CAL в этом случае называется графиком рынка капитала, или CML. У всех инвесторов имеется рыночный портфель M в качестве их оптимального рискованного портфеля. Разница между ними заключается лишь в том, какую сумму они инвестируют в этот портфель в сравнении с инвестицией в безрисковый актив.
3. Премия за риск для рыночного портфеля (равновесная премия за риск) пропорциональна его дисперсии и типичной степени неприятия риска инвестором. Математически это выражается:
E(rM) – rf = A* σM2 , (10.11)
где σM – среднеквадратическое отклонение ставки доходности рыночного портфеля;
А* – фактор, представляющий степень неприятия риска средним инвестором.
4. Премия за риск отдельных активов пропорциональна премии за риск рыночного портфеля (M) и коэффициенту «бета»(β) соответствующего актива. Это означает, что ставка доходности рыночного портфеля является единственным учитываемым фактором рынка ценных бумаг. Коэффициент "бета" определяет меру, в которой доходность акций соответствуют доходности рыночного портфеля. С формальной точки зрения, "бета" представляет собой тангенс угла наклона (т.е. отношение дополнительной доходности акции к дополнительной рыночной доходности) графика регрессии доходности акций от доходности рыночного портфеля. Иными словами, коэффициент "бета" представляет собой чувствительность доходности акций к изменениям доходности всего рынка.
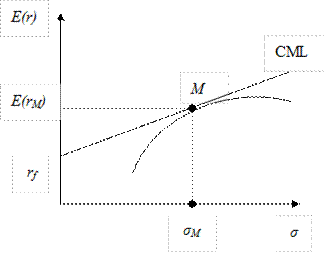
Рис.10.14. Эффективная граница и CML.
Учитывая все допущения САРМ, нетрудно понять, почему все инвесторы должны располагать идентичными рискованными портфелями. Если все инвесторы используют один и тот же критерий "риск-доходность", применяют его к одной и той же совокупности ценных бумаг, используют одинаковый временной горизонт, используют одну и ту же методику анализа ценных бумаг и сталкиваются с одними и теми же налоговыми последствиями, все они должны прийти к одному и тому же выводу относительно оптимального рискованного портфеля. Иными словами, все они строят идентичные эффективные границы и находят один и тот же "касательный" портфель на графике CAL, исходящий из ставки доходности безрисковых активов, которые имеют нулевое среднеквадратическое отклонение.
САРМ основывается на предположении, что соответствующая премия за риск какого-либо актива будет определяться его «вкладом» в общий риск портфеля. Интерес для инвестора представляет риск портфеля, который определяет величину премии за риск.
Нам известно, что с помощью диверсификации несистематический риск можно уменьшить до сколь угодно низкого уровня; следовательно, инвесторы не рассчитывают на получение премии в качестве компенсации за принятие на себя несистематического риска. Они требуют лишь компенсации за принятие на себя систематического риска, который невозможно диверсифицировать. Нам известно также, что "вклад" отдельной ценной бумаги в риск крупного диверсифицированного портфеля зависит лишь от ее систематического риска, определяемого β. Таким образом, не удивительно, что премия за риск некоторого актива пропорциональна коэффициенту "бета" этого актива; если, например, вы удвоите систематический риск какой-либо ценной бумаги, то должны удвоить и ее премию за риск, чтобы инвесторы по-прежнему были готовы держать у себя эту акцию. Следовательно, отношение премии за риск к коэффициенту "бета" должно быть одинаковым для любых двух ценных бумаг или портфелей.
Самым известным выражением САРМ является уравнение «ожидаемая доходность – коэффициент «бета», показывающее ожидаемые ставки доходности отдельных акций в рыночном рискованном портфеле:
E(rS) = rf + βS [E(rM) – rf], (10.12)
где E(rS) – ожидаемая доходность ценной бумаги (акции S);
rf – ставка доходности безрисковых активов;
βS – фактор «бета» акции S;
E(rM) – ожидаемая доходность рыночного портфеля.
Главный вывод модели САРМ – премия за риск ценных бумаг, их ожидаемая (избыточная) доходность пропорциональны коэффициенту «бета».
Уравнение «ожидаемая доходность-коэффициент "бета"» в САРМ играет чрезвычайно важную роль. Исходя из него, мы предполагаем, например, что премия за риск акции с высокой дисперсией, но относительно низким значением β, равным 0,5, составляет одну треть премии за риск ценной бумаги с низкой дисперсией β которой равняется 1,5. Таким образом, уравнение (10.12) является количественным выражением вывода, о том, что для инвесторов, которые могут диверсифицировать свой портфель, имеет значение лишь систематический риск, и что систематический риск измеряется коэффициентом "бета" соответствующей акции.
Индексная модель
Факторная модель (индексная модель – частный случай факторной) представляют собой статистическую модель, предназначенную для сопоставления влияния риска, специфического для конкретной фирмы, и систематического риска на доходность ценной бумаги.
Первым, кто использовал факторную модель для объяснения преимуществ диверсификации, был лауреат Нобелевской премии – Уильям Ф. Шарп.
У САРМ есть два ограничения:
1) предположение о существовании теоретического рыночного портфеля, который включает все активы (недвижимость, зарубежные акции и т.п.);
2) рассматриваются ожидаемые, а не фактические ставки доходности.
Практической реализацией САРМ является индексная модель, которая использует фактические, а не ожидаемые ставки доходности.
Обозначим премию за риск (см. главу 9) или избыточную (дополнительную) доходностьакции, которая является превышением ставки доходности над безрисковой ставкой, символом Ri , причем Ri = ri - rf . Эту избыточную доходность можно разбить на три составляющие:
Ri = E(Ri) + βiM + ei . (10.13)
В уравнении (10.13) E(Ri) представляет собой ожидаемую избыточную доходность за период владения (HPR) в начале этого периода. Следующие два члена отражают влияние двух источников неопределенности. M выражает рыночные или макроэкономические факторы в течение периода владения. βi – чувствительность данной акции к макроэкономическому (рыночному) фактору (систематическому риску). ei – это воздействие непредсказуемых факторов, специфических для конкретной фирмы. Как M, так и ei характеризуются нулевыми ожидаемыми значениями, поскольку каждый из этих членов представляет воздействие непредсказуемых событий, которое, по определению должно сводиться к нулю. Коэффициент βi разный для разных ценных бумаг, поскольку он показывает чувствительность i-ой ценной бумаги к макроэкономическим событиям.
Описание доходности акций с помощью факторной модели не представляет особой ценности, если невозможно указать способ "измерения" фактора, который влияет на доходность. Один вполне очевидный подход к решению этой проблемы заключается в использовании значения доходности какого-либо широкого фондового индекса, например S&P 500, в качестве "представителя", отражающего действие общего макроэкономического фактора. Если исходить из такого предположения, то для определения направления макроэкономических воздействий в любой период времени можно воспользоваться избыточной доходностью по сравнению с избыточной доходностью рыночного индекса, RM.
Индексная модель позволяет разделить достигнутую ставку доходности той или иной акции на макро- (систематический) и микро- (специфический) компоненты как это показано в уравнении (10.11). Избыточная ставка доходности каждой ценной бумаги представляет собой сумму трех компонентов:
1. Избыточная доходность акции при избыточной рыночной доходности равной нулю – αi .
2. Компонент доходности, вызванный «движениями» рынка в целом (представлен индексом RM); βi – чувствительность соответствующей акции к рыночным изменениям.
3. Компонент доходности, связанный с неожиданными событиями, которые касаются только этой акции (специфическими для конкретной фирмы).
Таким образом, избыточную доходность акций можно представить в следующем виде:
Ri = αi + βi RM + ei . (10.14)
Поскольку компонент доходности, специфический для этой фирмы, не коррелирован с рыночной доходностью, дисперсию избыточной доходности акций можно представить в следующем виде:
Дисперсия (Ri) = Дисперсия (αi + βi RM + ei) = Дисперсия (βi RM) + Дисперсия (ei) =
= 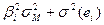 = (10.15)
= (10.15)
= Систематический риск + Специфический риск
Таким образом, совокупная изменчивость доходности каждой акции зависит от двух компонентов.
1. Изменчивость, связанная с неопределенностью, общей для всего рынка. Этот систематический риск относится к неопределенности RM. Обратите внимание на то, что систематический риск каждой акции зависит как от изменчивости RM (т.е. σM2), так и от чувствительности этой акции к колебаниям RM. Эта чувствительность измеряется коэффициентом "бета" (βi).
2. Дисперсия, связанная с факторами риска, специфическими для данной фирмы, действие которых измеряется величиной ei. Это дисперсия в той части доходности акций, которая не зависит от состояния рынка в целом.
Эта модель весьма удобна поскольку позволяет соотнести доходность ценной бумаги с биржевым рыночным индексом, которому доверяют инвесторы.
«Бета»
«Бета» – измеритель недиверсифицируемого, или рыночного, риска; показывает, как реагирует курс ценной бумаги на рыночные силы: чем более отзывчив курс ценной бумаги на изменения рынка, тем выше «бета» для этой ценной бумаги. «Бета» рассчитывают, опираясь на взаимосвязь фактической доходности ценных бумаг и фактической рыночной доходности. Рыночная доходность обычно измеряется как средний показатель доходности всех (или большой выборки) акций. Средняя доходность всех акций, входящих в составной фондовый индекс «Standard and Poor’s 500" или какие-либо другие всеобъемлющие фондовые индексы, наиболее часто используется для измерения рыночной доходности. «Бета» для всего фондового рынка равен 1; все другие значения «бета» рассматриваются по отношению к этой величине. Коэффициент регрессии «бета» измеряет относительную неустойчивость доходности конкретной ценной бумаги или портфеля в сравнении с репрезентативным показателем доходности фондового рынка.
«Бета» акции может быть вычислен с использованием следующих уравнений:
β = COVsm / VARm (10.16)
или
COVsm = ρsm • σs • σm , VARm= σ2m(10.17)
После сокращения подобных членов имеем:
β = ρsm • σ s / σm, (10.18)
где COVsm – ковариация доходности акции «s» относительно избранного индекса фондового рынка «m»:
COVsm = 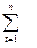 (st – š) • ( mt –
(st – š) • ( mt – 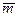 ) / ( n-1) , (10.19)
) / ( n-1) , (10.19)
где st, и mt – доходность акции и фондового индекса для периода t соответственно;
šи 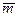 –средняя доходность акции и фондового индекса за период наблюдений;
–средняя доходность акции и фондового индекса за период наблюдений;
σ2m– дисперсия индекса доходности фондового рынка за период наблюдений;
σm- среднеквадратичное отклонение индекса доходности фондового рынка за период наблюдений;
σs - среднеквадратичное отклонение доходности акций за период наблюдений;
ρsm- коэффициент корреляции между доходностью акции и рыночной доходностью на базе индекса фондового рынка за период наблюдений.
Значение «бета» портфеля равно средневзвешенной «бета» всех акций в портфеле:
βпортфеля = ∑ ωi βi, (10.20)
где ωi– удельный вес соответствующей акции в портфеле.
Если портфель уже диверсифицирован, первое, что должно заботить инвестора, – это уровень его недиверсифицируемого риска. Мы можем измерить этот уровень с помощью уравнения регрессии с «бета»:
ri,t= ai + (β * rm,t), (10.21)
где ri,t– доходность ценной бумаги i или портфеля iв момент времени t;
ai – свободный член регрессии;
β— коэффициент регрессии "бета";
rm,t— доходность рыночного портфеля в момент времени t.
Понятие неустойчивости характеризует абсолютную величину колебаний доходности ценной бумаги или портфеля. Напротив, «бета» измеряет относительные колебания доходности ценной бумаги или портфеля в сравнении с индексом рыночной доходности; по сути, он отражает относительное изменение доходности акции или портфеля ценных бумаг в сравнении с динамикой рыночной доходности, измеренной на основе индекса. «Бета» акций широко используются на практике, так как информацию о них легко получить в брокерских фирмах и инвестиционных консультационных агентствах, например "Вэлью Лайн".
Использование и интерпретация «бета»
Полезность информации, заключенной в параметре «бета», зависит от того, насколько хорошо уравнение регрессии объясняет колебания доходности. Коэффициент детерминации (R2) измеряет объясняющую способность регрессионного уравнения. Он показывает, насколько процентов изменение зависимой переменной (доходность отдельной ценной бумаги ri,t) объясняется заданным соотношением с независимой (рыночной) переменной, которая обозначена rm,t .R2 может изменяться в интервале от 0 до 1. Если уравнение регрессии имеет величину R2, равную 0, это означает, что изменения доходности ценной бумаги совершенно (на 0%) не объясняются взаимосвязью с фондовым рынком. Значение коэффициента детерминации (R2), равное 1, говорит об абсолютной (100%-й) корреляции между ценной бумагой и рынком.
В табл. 10.1 показаны некоторые значения «бета» и их соответствующая интерпретация. Как можно видеть, «бета» имеет как положительное, так и отрицательное значение, хотя почти все фактические значения «бета» обычно положительные, и большинство акций имеет «бета» в диапазоне от 0,5 до 1,75.
Таблица 10.1
Выборочные значения «бета» и их интерпретация

«Бета» гораздо более полезен при объяснении колебаний в доходности портфеля, нежели отдельной ценной бумаги. Хорошо диверсифицированный портфель акций будет иметь коэффициент детерминации для регрессионного уравнения около 0,9. Это означает, что на 90% колебания курсов ценных бумаг портфеля объясняются изменениями на рынке акций в целом. В расчетах коэффициентов "бета" индивидуальных ценных бумаг (при составлении и решении регрессионного уравнения) параметр R2 имеет достаточно широкий спектр значений, но, как правило, находится в интервале от 0,2 до 0,5. Другие факторы (в частности, диверсифицируемый риск) также вызывают колебания курсов отдельных активов. Однако когда ценные бумаги объединены в хорошо диверсифицированный портфель, большая часть колебаний доходности этого портфеля вызвана движением всего фондового рынка.
Экономическая интерпретация «бета» может помочь понять его значимость. Если портфель имеет величину «бета», равную +1, то изменение его нормы доходности равно изменению доходности для рынка в целом. Это означает, что у портфеля с таким значением «бета» доходность, как правило, будет расти на 10%, если доходность рыночного портфеля акций в целом возросла на 10%. Естественно, если рыночная доходность упадет на 6%, то доходность портфеля с фактором «бета», равным +1, уменьшится в той же степени. В таблице 10.2 показана ожидаемая доходность для трех различных значений «бета» в двух ситуациях: рыночная доходность увеличивается на 10% или уменьшается на ту же величину. Портфель, имеющий значение «бета», равное 2, вдвое более изменчив, чем общий рыночный портфель. Когда рыночная доходность увеличивается на 10%, доходность такого портфеля увеличивается вдвое, т.е. на 20%. Понятно, что при обратной тенденции доходность данного портфеля упадет на 20%.
Таблица 10.2
«Бета» портфеля инвестиций и соответствующие изменения доходности
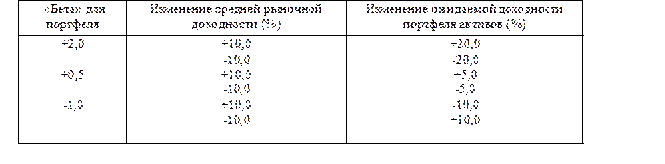
Расчет β
| Показатели | Низкий | Средний | Высокий | ||||||
| 0,50 | 0,63 | 0,75 | 0,88 | 1,00 | 1,25 | 1,50 | 1,75 | 2,00 | |
Факторы финансового риска:
| + | + + + | + + + | + + + + | + | + + | + | + + + | |
| количество наблюдений | |||||||||
| Взвешенный итог: | 0,63 | 2,25 | 2,64 | 4,0 | 1,25 | 3,0 | 1,75 | 6,0 | |
| Итого: 21,52 баллов, Итого наблюдений:18 β=21,52:18=1,196 |
Такой портфель можно считать относительно высоко рискованным и высокодоходным. Если значение «бета» равно 0,5, то портфель можно рассматривать как относительно низко рискованный и низко доходный – консервативный портфель для инвесторов, которые желают получать инвестиционный доход при низком риске. Он вдвое менее изменчив, чем рынок. Если портфель имеет величину «бета», равную -1, это говорит о том, что его доходность меняется в направлении, противоположном рынку. На рынке «медведей» инвесторы будут, вероятно, предпочитать портфель с отрицательным значением «бета», поскольку стоимость инвестиции этого типа растет, когда рынок акций падает, и наоборот. Однако подобрать ценные бумаги с отрицательной величиной «бета» не так просто. Большинство акций имеет положительный коэффициент корреляции с рынком, поскольку их доходность тяготеет к движению в том же направлении, что и весь рынок акций.
Дата добавления: 2017-01-29; просмотров: 1733;
