Ожидаемый доход и вариация портфеля P1.
Если портфель Р1 состоит из Х бумаг А и (1-Х) бумаг В, то:
1. Доходность портфеля:
RP1 = Х * RA + (1-Х) * RB; (10.1)
ожидаемая доходность:
Е(RP1) = Х * E(RA) + (1-Х) * E(RB); (10.2)
Е(RP1 ) = 0,6 * 8,15 + 0,4 * 6,6 = 2,445 + 4,62 = 7,53.
2. Ковариация (Cov) вычисляется примерно так же, как дисперсия. Однако вместо того, чтобы вычислять типичное отклонение доходности актива от ее ожидаемого значения, нужно измерить степень, в которой колебания доходностей этих двух активов стремятся усиливать или, наоборот, взаимно компенсировать друг друга. Ковариация – это произведение отклонения активов от ожидаемой доходности:
Cov(RA,RB) =∑[ps * (RAs-E(RA) ) * (RBs-E(RB))]. (10.3)
Иногда мы не знаем ковариацию, но мы можем найти коэффициенты корреляции и две вариации. В этом случае вы можете найти ковариацию следующим образом:
Cov(A,B) = σAB = Corr(A,B) * SD(A) * SD(B), (10.4)
или в стандартных символах:
Сov(A,B ) = ρAB * σA * σB. (10.5)
Ковариация может быть больше, меньше и равна нулю, что иллюстрирует рис. 10.5.
Положительная ковариация свидетельствует об усилении взаимных колебаний двух активов, отрицательная ковариация означает, что колебания доходностей двух активов компенсируют друг друга.
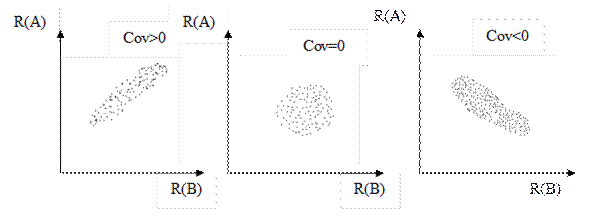 Рис.10.5. Варианты ковариаций доходностей двух активов.
Рис.10.5. Варианты ковариаций доходностей двух активов.
Различные варианты ковариаций доходностей двух активов приводят к различным результатам диверсификации. Отрицательная ковариация означает различную реакцию доходностей двух активов на изменение условий инвестирования (сценариев). Такое их поведение дает надежду на то, что портфель составленный из таких активов будет менее подвержен риску инвестирования.
3. Корреляция (Corr) является нормальным линейным распределением, коэффициент корреляции (ρ) определяем как:
ρАB = Соv (RA,RB) / σА σВ. (10.6)
4.Дисперсия портфеля:
Var(RP1) = σP12 = [X * σA +(1- X) * σB ]2 = Х2 * σA2 + (1-Х)2 * σB2 + 2Х * (1-Х) * σAB = = Х2 * Var(RA)+(1-Х)2 * Var(RB)+2X * (1-Х) * Cov(RA,RB), (10.7)
таким образом, σP12 = Х2 * σA2 + (1-Х)2 * σB2 + 2Х * (1-Х) * σAB (10.8)
Иначе это можно рассчитать через ковариационную матрицу.
Ковариационная матрица выглядит следующим образом:
A B
A Var(RA) Cov(RA,RB)
B Cov(RA,RB) Var(RB)
A B
A 4,3275 -5,04
B -5,04 5,94
При X = 0,6 и (1-Х) = 0,4 дисперсию портфеля (Var(RP1)) можно найти из следующей матрицы:
X (0,6) 1-X (0,4)
X (0,6) 4,3275 -5,04
1-X (0,4) -5,04 5,94
Затем берем каждую ячейку ковариационной матрицы умножаем на колонку и строчку пропорций ценных бумаг в портфеле:
1,5579 -1,2096
-1,2096 0,9504
Суммируя все строки и колонки вместе, получаем дисперсию доходности портфеля P1:
Var (RP1) = 0,6*0,6*4,3275+0,6*0,4*(-5,04)+0,4*0,6*(-5,04)+0,4*0,4*5,94 = 0,0891.
Мы можем получить волатильность (стандартное отклонение) портфеля P1 путем извлечения квадратного корня из дисперсии портфеля P1:
Vol(RP1) =√0,0891 = 0,2985, или
Vol(RP1) = 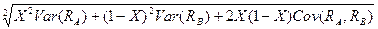 , (10.9)
, (10.9)
т.е. 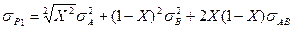 . (10.10)
. (10.10)
Vol(RP1) = 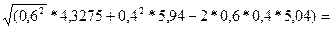
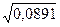 = 0,2985.
= 0,2985.
Все расчеты можно легко произвести в EXCEL.
| ps | RA | RB | psRA | psRB | RA-E(RA) | RB-E(RB) | (RA-E(RA))2 | (RB-E(RB))2 | ps(RA-E(RA))2 | ps(RB-E(RB))2 | (RA-E(RA)) (RB-E(RB)) | ps(RA-E(RA)) (RB-E(RB)) |
| 0,25 | 2,75 | 0,75 | 2,85 | -3,6 | 8,1225 | 12,96 | 2,0306 | 3,24 | -10,26 | -2,565 | ||
| 0,3 | 2,7 | 1,8 | 0,85 | -0,6 | 0,7225 | 0,36 | 0,2168 | 0,108 | -0,51 | -0,153 | ||
| 0,45 | 2,7 | 4,05 | -2,15 | 2,4 | 4,6225 | 5,76 | 2,0801 | 2,592 | -5,16 | -2,322 | ||
| 8,15 | 6,6 | 4,3275 | 5,94 | -5,04 | ||||||||
| =E (RA) | =E (RB) | =Var (RA) SD(RA)= 2,0803 | =Var (RB) SD(RB)= 2,43721 | =Cov (RA,RB) corr(RA, RB)= -0,99407 |
Этот пример показывает абсолютно отрицательную корреляцию.
Как видно диверсификация портфеля из двух отрицательно коррелированных активов дает значительное снижение риска (σP1 = 0,2985), в сравнении с рисками каждого из активов в отдельности (σA = 2,0803, σB = 2,43721), при относительном «усреднении» ожидаемой доходности (7,53% против 8,15% для ценной бумаги А и 6,6% для актива В).
Графически ожидаемая доходность и риск портфеля Р1 при любой комбинации активов (пропорции, любом значении Х) представлена на рисунке 10.6.
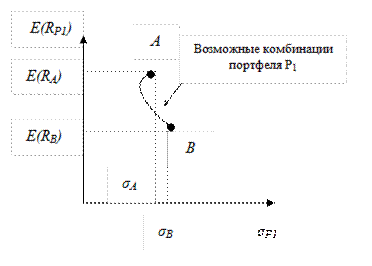
Рис. 10.6. Возможная доходность и риск портфеля P1 ,состоящего из комбинации двух активов A иB.
В следующем примере, в котором имеет место положительная корреляция (хотя не абсолютная), присутствуют бумаги C и D. В этом примере видно, что даже положительно коррелированные ценные бумаги приводят к положительным результатам диверсификации портфеля.
| ps | RC | RD | psRC | psRD | RC-E(RC) | RD-E(RD) | (RC- E(RC))2 | (RD-E(RD))2 | ps(RC-E(RC))2 | ps(RD-E(RD))2 | (RC- E(RC)) (RD-E(RD)) | ps(RC- E(RC)) (RD-E(RD)) |
| 0,25 | 2,25 | 2,25 | 5,063 | 2,25 | 1,26563 | 6,75 | 1,6875 | |||||
| 0,5 | 4,5 | -0,75 | 0,563 | 0,28125 | ||||||||
| 0,25 | 1,5 | 1,5 | -3 | -0,75 | 0,563 | 2,25 | 0,14063 | 2,25 | 0,5625 | |||
| 6,75 | 4,5 | 1,6875 | 2,25 | |||||||||
| =E (RC) | =E (RD) | =Var (RC) SD(RC) =2,1213 | =Var (RD) SD(RD)= 1,29904 | = Cov (RC,RD) corr (RC, RD)= 0,8164 |
Дата добавления: 2017-01-29; просмотров: 1088;
