Современная теория эффективного портфеля

Гарри Марковиц впервые сформулировал свои идеи в 50-х годах. Они составили основу современной портфельной теории, и с тех пор многие другие исследователи и инвестиционные эксперты внесли свой вклад в ее развитие до нынешнего продвинутого уровня.

В экономике часто встречаются ситуации, когда субъект (физическое лицо или фирма, инвестор) должны выбрать одну из альтернатив. Существует экономическая теория, которая занимается изучением процесса выбора, используя так называемую функцию полезности. В теории портфеля функция полезности выражает предпочтения субъекта при определенных отношениях к риску и представлениях об ожидаемых доходностях. В графической форме функцию полезности отражают известные кривые безразличия. Если на оси абсцисс откладывается значение риска, и по ординате – ожидаемые доходности, то чем выше лежит кривая безразличия, тем больше полезность, поскольку по вертикали отложены доходности (рис.10.2).

При формировании портфеля следует различать рискованные и безрисковые активы. Рискованные активы – это активы, доходность которых в будущем неопределенна. Существуют активы, будущая доходность которых известна. Такие активы называются безрисковыми, как правило, это краткосрочные правительственные облигации.

Принимая решение о приобретении портфеля, инвестор должен обращать внимание на ожидаемую доходность и стандартное отклонение каждого портфеля.

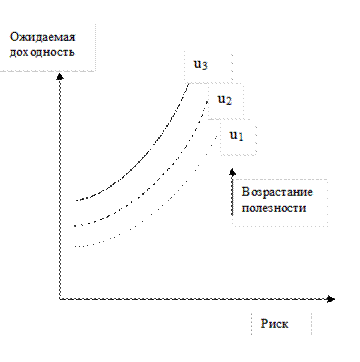
Рис.10.2. Кривые безразличия в теории портфеля.

Все портфели, лежащие на одной заданной кривой безразличия, являются равноценными для инвестора.

Доходность портфеля легко определить по доходности входящих в него ценных бумаг, как сумма всех возможных ставок доходности ценных бумаг, умноженных на соответствующую вероятность их получения. Но риск портфеля более сложен для определения. Доходность портфеля – это взвешенная средняя доходностей ценных бумаг, входящих в портфель.

Риск одного актива измеряется дисперсией или среднеквадратическим отклонением доходов по этому активу, а риск портфеля дисперсией или среднеквадратическим отклонением доходов портфеля. Однако чтобы измерить риск портфеля, нужно знать не только вариацию (дисперсия) доходов отдельных ценных бумаг, но и степень, с которой доходы пар ценных бумаг колеблются вместе. Необходимо знать ковариацию или же корреляцию доходов каждой пары активов в портфеле.

Итак, диверсификация Марковица включает конструирование портфелей с низкой парной корреляцией между ЦБ входящими в портфель. Такой набор бумаг в портфеле формирует приемлемое соотношение между риском и доходностью портфеля. Единицы с высоким доходом для заданного уровня риска (или минимальный риск для заданного уровня дохода) формирует эффективный набор или границу.

Современная портфельная теория использует несколько основных статистических показателей для обоснования портфельной стратегии. Один из таких показателей – квадрат стандартного отклонения, или дисперсия доходности актива. Дисперсия служит мерой разброса значений случайной величины вокруг ее среднего значения. Для доходности (как случайной величины) дисперсия, оценивающая степень отклонения возможных конкретных значений от средней или ожидаемой доходности, служит мерой риска, связанного с данной доходностью.

Второй – корреляция доходности пары ценных бумаг или отдачи ценной бумаги и рынка в целом. Корреляция измеряет связь (если таковая имеет место) между двумя числовыми рядами, представляющими определенный вид данных – доходности ценных бумаг. Если два ряда движутся в одном направлении, то они положительно коррелированны, если в противоположных – отрицательно. Степень зависимости данных одного ряда от другого измеряется коэффициентом корреляции, который варьирует от +1 для абсолютно положительно коррелированных рядов до -1 для абсолютно отрицательно коррелированных рядов. Абсолютно положительно коррелированные ряды изменяются параллельно друг другу, а абсолютно отрицательно коррелированные – в прямо противоположных направлениях. При создании портфеля по концепции современной портфельной теории большое внимание уделяется корреляции между показателями доходности различных активов.

Рисунок 10.3. иллюстрирует относительную корреляцию норм доходности для двух портфелей (каждый из которых содержит по две ценные бумаги). Левый график показывает изменение нормы доходности двух ценных бумаг X и Y во времени. Очевидно, что здесь наблюдается строгая положительная корреляция показателей их норм доходности, поскольку они изменяются параллельно. Правый график изображает доходность ценных бумаг Х и Z. Их нормы доходности характеризуются строго отрицательной корреляцией, так как они изменяются в противоположных направлениях. Диверсификация согласно концепции современной портфельной теории достигается при такой комбинации ценных бумаг, когда составляющие портфеля имеют отрицательную (или слабоположительную) корреляцию между нормами доходности. Следовательно, при выборе ценных бумаг в качестве решающего фактора современная портфельная теория выдвигает статистическую диверсификацию, т.е. отрицательную или низкую положительную корреляцию доходности. Портфель, состоящий из ценных бумаг Х и Y, плохо диверсифицирован, так как характеры динамики доходности всех ценных бумаг почти совпадают. Совмещение в портфеле ценных бумаг Х и Z ведет к существенно лучшей диверсификации благодаря высокой отрицательной корреляции их доходности.

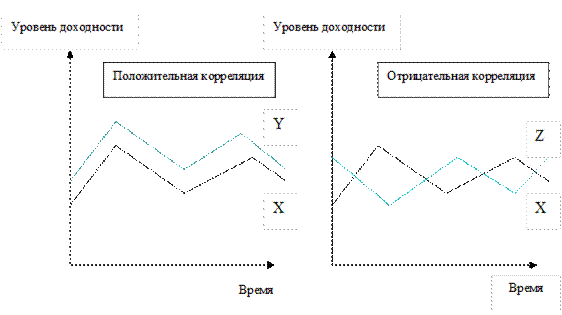
Рис.10.3. Корреляция доходности ценных бумаг.

Доходность активов Х и Y имеет высокую положительную корреляцию и, таким образом, эти активы не предоставляют возможностей для диверсификации. Доходность активов Х и Z имеет высокую отрицательную корреляцию, следовательно, эти активы создают возможность выигрыша от диверсификации. Чем ниже положительная (или чем выше отрицательная) корреляция доходности двух активов, тем более существенный выигрыш можно получить от диверсификации с точки зрения риска и доходности.