Ожидаемый доход и дисперсия портфеля P2.
Если мы имеем P2 = (0.25)C+(0.75)D, то получаем
E(RP2)=(0,25)E(RC)+(0,75)E(RD)=(0,25)(9)+(0,75)(6,75) = 0,25*9+0,75*6,75 = 7,3125;
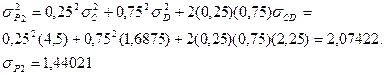
Мы можем использовать таблицу в EXCEL для подсчета этой формулы:
| ps | RC | RD | RP2 | psRP2 | RP2-E(RP2) | (RP2-E(RP2))2 | ps(RP2-E(RP2))2 |
| 0,25 | 9,75 | 2,44 | 2,438 | 5,94141 | 1,4854 | ||
| 0,5 | 6,75 | 3,38 | -0,56 | 0,31641 | 0,1582 | ||
| 0,25 | 1,5 | -1,31 | 1,72266 | 0,4307 | |||
| 7,31= E(RP2) | 2,0742= Var(RP2) SD(RP2)= 1,4402 |
Графически ожидаемая доходность и риск портфеля Р2 при любой комбинации активов представлена на рисунке 10.7.
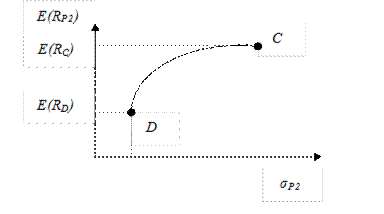
Рис.10.7 . Возможная доходность и риск портфеля P2 ,состоящего из комбинации двух активов C иD.
Активы С и D хотя и имеют положительное значение корреляции доходностей, имеют благоприятные перспективы комбинирования их в инвестиционном портфеле. Поскольку ни один из активов не доминирует по отношению к другому ( актив С имеет большую ставку доходности, но и больший уровень риска), нет явного предпочтения при составлении портфеля ни из одного из них. Наиболее приемлемый результат дает комбинация из этих двух активов в портфеле. Хотя в этом случае преимущества диверсификации не так очевидны, как при формировании портфеля P1.
Совокупность инвестиционных возможностей, которые обеспечиваются портфелями, сформированными с помощью двух активов, доступных инвесторам и представленных в различных пропорциях и из различных видов активов (акций, облигаций, денежных активов) показаны на рисунке 10.8
Точки на совокупности инвестиционных возможностей, показанной на рисунке 10.8 можно найти путем изменения пропорций инвестирования и вычисления итоговых значений ожидаемой доходности и стандартного отклонения с помощью уравнений (10.2) и (10.10).
Инвесторы предпочитают портфели с высокими значениями ожидаемой доходности и низкой изменчивостью (волатильностью) доходности. Если все инвесторы предпочитают портфель P1, а не P2, считается, что портфель P1, доминирует над портфелем P2. Это происходит в том случае, если средняя доходность портфеля P1, окажется выше, чем у портфеля P2, а дисперсия портфеля P1, – ниже, чем у портфеля P2. Портфель P3 доминирует над портфелем P4, поскольку он имеет более высокую ожидаемую доходность, при меньшем риске. Портфели расположенные ниже портфеля с минимальной дисперсией (портфеля P1,), можно сразу же отвергнуть как неэффективные.
Наилучший вариант среди портфелей выше портфеля P1, на этой кривой не столь очевиден, поскольку на этом участке более высокие значения ожидаемой доходности сопровождаются более высоким риском. Наилучший вариант определяется склонностью инвестора к риску.
На этом отрезке (выше портфеля P1,) имеет место положительная корреляция между ставками доходности. Известно, что низкая корреляция способствует диверсификации. Идеальная положительная корреляция (ρ=1) является единственным случаем, когда диверсификация не приносит никакой выгоды. Если ρ<1, диверсификация дает положительный результат.
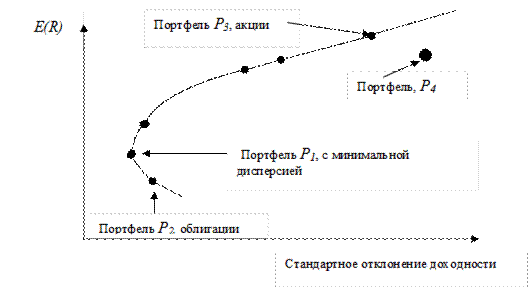
Рис.10.8. Совокупность инвестиционных возможностей для портфеля из двух активов.
Точки на совокупности инвестиционных возможностей можно найти путем изменения пропорций инвестирования. Эффективные инвестиционные пропорции двух активов способны еще больше снизить риск портфеля в дополнение к диверсификации.
Отрицательная корреляция между двумя активами также возможна и выгоды от применения диверсификации в этом случае оказываются еще большими. При идеальной отрицательной корреляции, т.е. ρ = -1 выгоды от применения диверсификации достигают своего максимума, в этом случае есть возможность получить пропорции портфеля, при которых стандартное отклонение доходности сокращается вплоть до нуля.
Рассмотрим теперь самый общий случай, когда у двух активов разные доходности и разные стандартные отклонения доходностей. Зависимость стандартного отклонения доходности такого портфеля от коэффициента корреляции и соотношения весов показана на рис. 10.9. На плоскости «доходность – риск» образуются эллипсы, каждому коэффициенту корреляции соответствует свой эллипс, точки на каждом эллипсе соответствуют разным соотношениям весов компонент. При полной корреляции, как положительной, так и отрицательной (ρ = ±1), эллипсы вырождаются в отрезки прямых линий.
На графике видно, что не только для отрицательных, но и для низких положительных корреляций существуют портфели, риск которых меньше, чем риск каждого из входящих в них активов. В самом деле, в данном примере уже для ρ = +0,5 при некоторых соотношений весов стандартное отклонение портфеля меньше, чем стандартное отклонение любого из активов. Добавляя к активу А некоторую долю актива В (с большей доходностью и более высоким риском) можно одновременно увеличить доходность портфеля и снизить его риск.
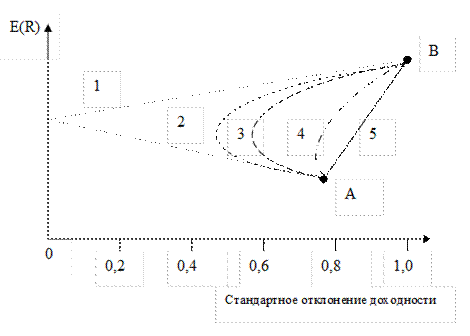
Рис. 10.9. Зависимость доходности портфеля из двух активов от коэффициента корреляции и соотношения весов.
На графике доходность и дисперсия второго актива вдвое выше. Различным вариантам корреляций между двумя активами А и В соответствуют различные линии ожидаемой доходности портфеля E(R):
1 – ρ = -1,0;
2 – ρ = -0,5;
3 – ρ = 0;
4 – ρ =+0,5;
5 – ρ =+1,0.
Дата добавления: 2017-01-29; просмотров: 876;
