Уравнения плоскопараллельного движения АТТ.

В кинематике уравнения движения плоского сечения:

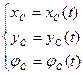
Три степени свободы.

Свободное тело: (нет связей).

Работают уравнения Лагранжа.

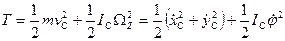
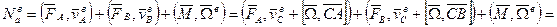
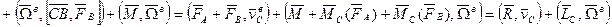
Суммарная мощность всех сил и моментов, приложенных к АТТ равна мощности главного вектора 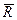системы сил, как если бы он был приложен к центру масс, и мощности главного момента всех сил, относительно центра масс.

=

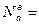
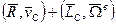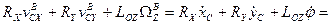
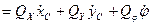
Обобщенные силы

, ,

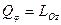
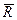( - главный вектор системы сил, 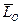- главный момент системы сил, приложенных к АТТ).

Запишем 3 уравнения Лагранжа:

,

,

,

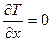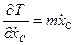
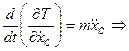
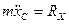
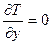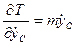
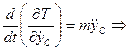
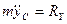
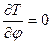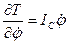
Следствие: Если АТТ может совершать только поступательное движение по оси 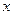, то это движение описывается одним уравнением: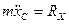

Если же АТТ совершает поступательное и вращательное движение, то 2 уравнения.

Уравнение вращения АТТ вокруг неподвижной оси.

Если тело вращается вокруг неподвижной оси, то оно имеет одну степень свободы. Его положение определяется одной координатой: углом поворота.

Составляя уравнение Лагранжа для тела с одной степенью свободы, получим уравнение вращения АТТ вокруг оси: 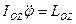или или .