Теперь рассмотрим неконсервативную систему.
Условие равновесия- принцип возможных перемещений (для систем с идеальными связями).
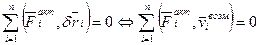
сумма элемент. сумма мощност. акт.
работ акт. сил вычисл. на возм. скор.

ДАНО:
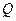 ,
, 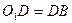
Найти:
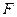 , чтобы система была в равновесии.
, чтобы система была в равновесии.
Решение: система с идеальными связями 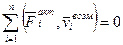
Идеальные связи:
В точке  - неподвижный шарнир.
- неподвижный шарнир. 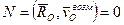 , так как
, так как 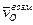 =0.
=0.
Аналогично в точке 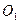 - неподвижный шарнир.
- неподвижный шарнир.
В точке 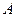 - подвижный внутренний шарнир.
- подвижный внутренний шарнир.
В точке 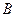 - подвижный внутренний шарнир.
- подвижный внутренний шарнир.
Силы, действующие во внутреннем подвижном шарнире на тела, соединенные этим шарниром, равны по величине и противоположны по направлению, а скорости в этих точках у тел равны между собой.
Суммарная мощность сил реакции в подвижном внутреннем шарнире =0.
Связи иделаьные.
Условие равновесия: 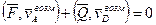 - принцип возможных перемещений.
- принцип возможных перемещений.
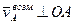
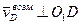
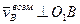 .
.
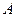 и
и 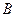 - точки АТТ.
- точки АТТ.
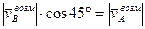
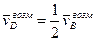
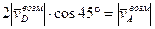
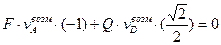 ,
, 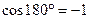 ,
, 


Уравнение равновесия неконсервативных систем (с идеальными голономными связями).

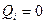 ,
, 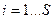 - число степеней свободы.
- число степеней свободы.
все обобщенные силы
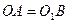 ,
, 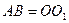 ,
, 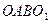 - параллелограмм.
- параллелограмм.
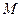 ,
, 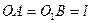 ,
,  - вес поршня.
- вес поршня.
Система с одной степенью свободы. Обобщенная координата- угол между осью 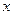 и
и 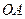
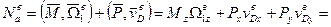 {
{  =0,
=0, 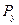 =
= 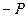 }
}
 =
= 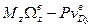 =
= 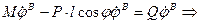

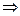
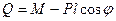

Уравнение равновесия: 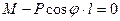
Если 3 степени свободы, то 3 уравнения равновесия.
БИЛЕТ 35.
Дата добавления: 2016-04-23; просмотров: 589;
