Вращение АТТ вокруг неподвижной оси.
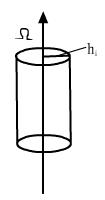
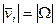

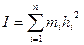
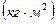

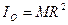
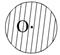
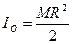

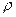 -радиус инерции.
-радиус инерции.
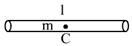
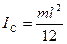
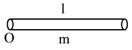
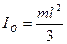
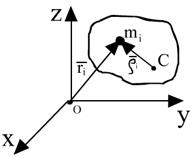
 - АТТ
- АТТ
 - центр масс АТТ
- центр масс АТТ
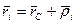
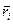 - радиус-вектор.
- радиус-вектор. 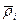 - относительно ц. масс.
- относительно ц. масс.
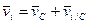
 +
+
+ 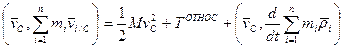
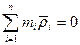
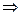
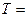
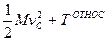 - Теорема Кёнига.
- Теорема Кёнига.
«Кинетическая энергия АТТ в произвольном движении равна сумме кинетической энергии центра масс, как если бы в нем была сосредоточена вся масса АТТ и кинетической энергии движения относительно центра масс».
Плоское движение:
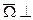 плоскости движения.
плоскости движения.
Движение относительно центра масс будет представлять собой движение вокруг оси 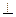 плоскости движения и проходящей через центр масс.
плоскости движения и проходящей через центр масс.
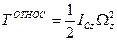

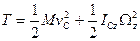
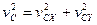
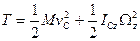
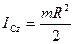
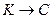 (90
(90 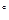 ,
, 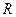 )
)
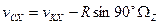
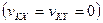
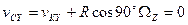
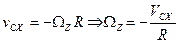
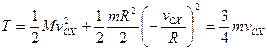
БИЛЕТ 26.
Системы сил называются консервативными, если работа этих сил не зависит от формы траектории, а определяется только начальной и конечной точкой. Работа консервативных сил по замкнутому контуру = 0.
Силы называются потенциальными, если существует такая скалярная функция, которая зависит или от радиуса вектора или от координат, что вектор силы 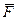 , действующей в точке
, действующей в точке 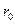 равен
равен 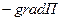 этой функции, или
этой функции, или 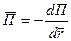 .
. 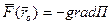 .
.
 .
.
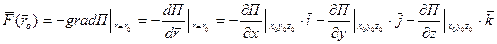
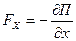 ,
, 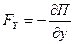 ,
, 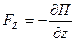 .
. 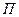 - потенциальная энергия, силовая функция.
- потенциальная энергия, силовая функция.
 .
.
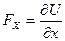 ,
, 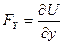 ,
, 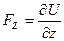 .
.
Если система сил потенциальна, то она является консервативной.
Найдем работу по перемещению из точки 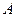 в точку
в точку 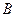 .
.
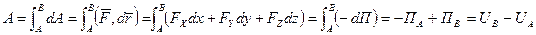
 .
.
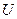 - потенциальная энергия. Работа не зависит от пути.
- потенциальная энергия. Работа не зависит от пути.
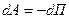 - приращение потенциальной энергии.
- приращение потенциальной энергии.
Из теоремы об изменении кинетической энергии для консервативных систем: 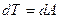 .
.
Если все внешние и внутренние силы консервативны, то 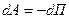 , а значит для консервативных систем:
, а значит для консервативных систем: 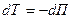
Полная механическая энергия 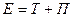 .
.
Теорема (об изменении полной механической энергии для консервативных систем):
Если система материальных точек консервативна, то ее полная механическая энергия есть величина постоянная:  .
.
БИЛЕТ 27.
Связями называется ограничение на движение материальной точки.

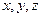
Плоский математический маятник. 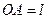 ,
, 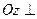 плоскости движения.
плоскости движения.
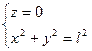
 Система материальных точек.
Система материальных точек.
Если бы они были свободны.

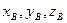
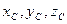
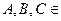 АТТ.
АТТ.
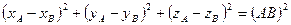
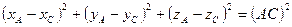
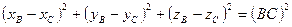 .
.
Аналитическая запись:
 ,
, 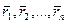 ,
, 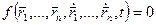
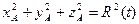 - уравнение связи для материальной точки, находящейся на поверхности сферы переменного радиуса.
- уравнение связи для материальной точки, находящейся на поверхности сферы переменного радиуса.
В зависимости от типа уравнений различаются и типы связей:
1). Стационарные связи(в уравнения которых не входит время). 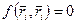
2). Нестационарные связи(в уравнения которых входит время). 
3). Односторонние связи 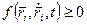
4). Двусторонние связи (выражаются уравнениями)
5). Геометрические связи (голономные).
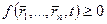 . Не содержат в качестве аргументов скорости точек.
. Не содержат в качестве аргументов скорости точек.
6). Дифференцируемые (не голономные связи).

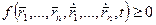
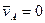
Возможные перемещения- перемещения, которые допускаются связями в данный момент времени.
 ,
, 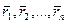 .
.
Двусторонние и голономные связи: 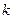 уравнений связи:
уравнений связи:
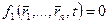
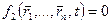
………..
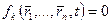
Вариации этих уравнений:
При фиксированном 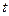
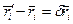
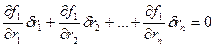
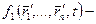
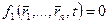

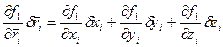


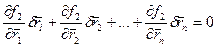 - уравнения для возможных перемещений.
- уравнения для возможных перемещений.
………..
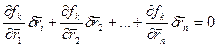
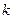 уравнений для
уравнений для 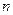 векторных неизвестных.
векторных неизвестных. 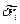 .
.
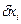 ,
,  ,
, 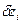 - возможные вариации в декартовых координатах.
- возможные вариации в декартовых координатах.
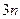 вариаций подчиняются
вариаций подчиняются 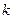 уравнениям связи
уравнениям связи 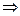 независимых вариаций декартовых координат остается
независимых вариаций декартовых координат остается 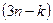 . Говорят, что система имеет
. Говорят, что система имеет 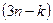 степеней свободы.
степеней свободы.

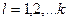 - уравнение для возможных перемещений
- уравнение для возможных перемещений 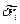 .
.
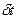 - воображаемый промежуток времени.
- воображаемый промежуток времени.
 . Уравнение для возможных скоростей:
. Уравнение для возможных скоростей: 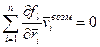
Возможная скорость- скорость,которая допускается связями в данный момент времени.
Рассмотрим пример, когда точка находится на сфере постоянного радиуса. Ее возможное перемещение как и возможная скорость должна быть направлена по касательной к сфере или 
радиус-вектору.
Действительная скорость- одна из возможных.

Теперь рассмотримслучай, когда точка находится на сфере переменного радиуса.

Действительная скорость= одна из возможных скоростей + одна из скоростей.
БИЛЕТ 28.
Рассмотрим систему материальных точек  , на которую наложены связи.
, на которую наложены связи.

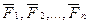 - силы, действующие на точки системы со строны внешних по отношению к системе сил, и внуренних. Они называются активными силами.
- силы, действующие на точки системы со строны внешних по отношению к системе сил, и внуренних. Они называются активными силами.
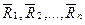 - силы реакции связей.
- силы реакции связей.
Аксиома освобождаемости от связей:
Связи, наложенные на систему можно отбросить, заменив
 их действие силами реакции связи.
их действие силами реакции связи.

Система свободных материальных точек но с силами реакции связи. Направление зависит от типа связей.
Дата добавления: 2016-04-23; просмотров: 1266;
