Качение без проскальзывания.
 , так как возможное перемещение в точках контакта с поверхностью = 0.
, так как возможное перемещение в точках контакта с поверхностью = 0.
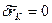
 4). Неподвижный цилиндрический шарнир.
4). Неподвижный цилиндрический шарнир.
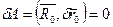
 5). Подвижный шарнир.
5). Подвижный шарнир.
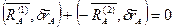
БИЛЕТ 29.
Рассмотрим систему 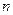 материальных точек, на которую наложены
материальных точек, на которую наложены 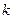 голономных связей. Из
голономных связей. Из 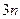 вариаций декартовых координат точек системы независимыми будут только
вариаций декартовых координат точек системы независимыми будут только 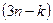 .
.
Это число и назовем числом степеней свободы системы.
Число степеней свободы = числу независимых возможных скоростей.
Если на систему наложены 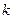 голономных связей, то возможно введение
голономных связей, то возможно введение 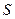 параметров
параметров
{ 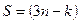 ,
, 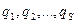 }, которые:
}, которые:
1). Полностью определяют положение системы
2). Не зависят друг от друга.
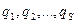 - обобщенные координаты.
- обобщенные координаты.
Обобщенные координаты- 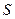 параметров, если они 1) и 2).
параметров, если они 1) и 2).
 Пример:
Пример:
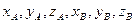

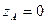 ,
, 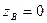
 - 4 уравнения голономных стацион. связей
- 4 уравнения голономных стацион. связей
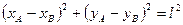
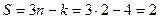
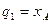 ,
, 
Обобщенные скорости:
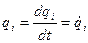
 - всего
- всего 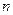
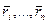
Если введены обобщенные координаты
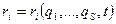
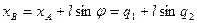
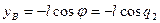
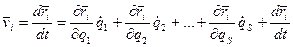
Скорость 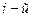 точки:
точки: 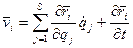
Если связи, наложенные на систему стационарные, то последнее слагаемое равно нулю.
При фиксированном 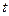 :
: 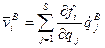 .
.
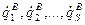 не зависят друг от друга.
не зависят друг от друга.
 ,
, 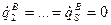
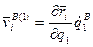
БИЛЕТ 30.
Обобщенные силы.
 ,
, 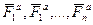 ,
, 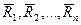 - силы реакции.
- силы реакции.
Пусть в системе введены обобщенные координаты: 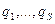 (
( 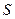 степеней свободы).
степеней свободы).
Возможное перемещение: 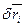 :
: 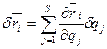 .
.
Тогда элементарная работа активных сил 

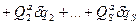 , где
, где 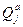 - обобщенная активная сила.
- обобщенная активная сила.
Обобщенные силы- коэффициенты в разложении элементарной работы активных сил по вариации обобщенных координат. 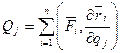
Размерность обобщенной силы зависит от размерности соотвествующей обобщенной координаты.
Если обобщенная координаты угловая, то соответствующая обобщенная сила имеет размерность  , то есть размерность момента.
, то есть размерность момента.
Обобщенная сила- скалярная величина.
Рассмотрим элементарную работу сил реакции связи.
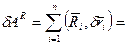
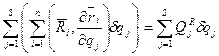 , где
, где 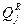 - обобщ.сила реакции.
- обобщ.сила реакции.
Если связи, наложенные на систему являются идеальными, то 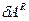 = 0
= 0 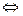
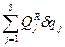 = 0
= 0 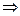
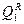 = 0,
= 0, 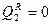 , …,
, …, 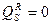 .
. 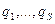 - обобщенные координаты, не зависят друг от друга.
- обобщенные координаты, не зависят друг от друга. 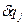 - независимы. Можно не говорить об обобщенных силах реакции в идеальных связях.
- независимы. Можно не говорить об обобщенных силах реакции в идеальных связях.
Рассмотрим систему материальных точек со связями:
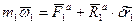

………
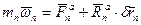
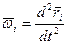 - угловая скорость
- угловая скорость 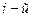 точки.
точки.
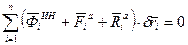
БИЛЕТ 31.
Принцип Даламбера:
БИЛЕТ 32.
Принцип Даламбера:
Сумма элементарных работ сил инерции, активных сил и сил реакции связи = 0. Если связи, наложенные на систему, идеальные, то 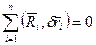 .
.
Принцип Даламбера для систем с идеальными связями: сумма элементарных работ и элементарных сил на возможных перемещениях = 0. 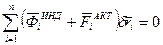 .
.
Пусть система материальных точек с идеальными связями находится в равновесии.
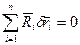 ,
, 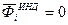 ,
, 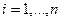 .
.
Принцип Даламбера: 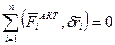 - прицип возможных перемещений.
- прицип возможных перемещений.
Необходимым и достаточным условием равновесие системы с идеальными связями является равенство нулю суммы элементарных работ активных сил на возможных перемещениях.
Принцип возможных перемещений- условие равновесия!!!!!!!!!!
Рассмотрим систему с идеальными связями.
Обобщенные координаты
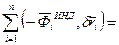
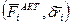

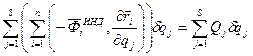 . Так как
. Так как 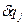 - независимы,
- независимы,
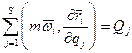 .
. 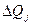 - вариация
- вариация 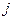 - й обобщенной координаты.
- й обобщенной координаты.
Следствие: 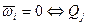 . Система с идеальными связями находится в равновесии тогда и только тогда, когда все обобщенные силы равны нулю.
. Система с идеальными связями находится в равновесии тогда и только тогда, когда все обобщенные силы равны нулю.
БИЛЕТ 33.
Доказательство уравнения Лагранжа 2-го рода.
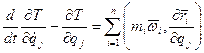 -?
-?
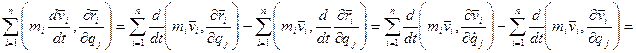
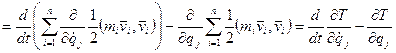 .
.
Дата добавления: 2016-04-23; просмотров: 1238;
