Главный вектор и главный момент системы сил.
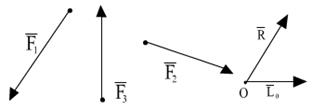
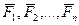
Главным вектором системы сил называется геометрическая сумма всех сил системы.
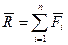
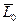 - сумма векторов элементов всех сил, взятых относительно точки O.
- сумма векторов элементов всех сил, взятых относительно точки O.
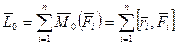 . При совершении этой операции допускается перенос всех векторов в точку O.
. При совершении этой операции допускается перенос всех векторов в точку O.
При изменении точки приведения системы сил главный вектор системы сил не изменяется, а главный момент меняется.
Изменение точки приведения:
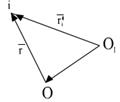
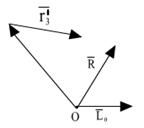
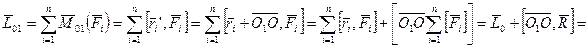
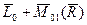
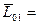
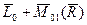 .
.
Главный момент системы относительно точки 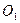 равен главному моменту системы относительно точки
равен главному моменту системы относительно точки 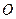 + моменту главного вектора относительно точки
+ моменту главного вектора относительно точки 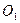 , если бы этот главный вектор был приложен к точке
, если бы этот главный вектор был приложен к точке 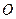 .
.
Условие равновесия системы сил: система сил или система АТТ, на которую действует система сил находится в равновесии тогда и только тогда, когда равны нулю главный вектор системы сил и главный момент системы сил.
Это условие сохраняется при изменении точки приведения.
БИЛЕТ 19.
Парой сил называется система двух сил, равных по величине и противоположных по направлению. Линии действия этих сил параллельны. Расстояние межу этими линиями действия сил называется плечом пары.
Плоскость, в которой лежат прямые называется плоскостью пары.
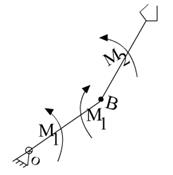
Теорема: момент пары сил не зависит от точки, относительно которой этот момент вычисляется. Момент пары сил равен моменту одной из сил, составляющих пару, относительно точки приложения другой.
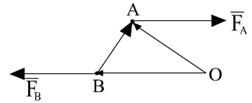
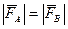
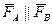
Момент пары сил: 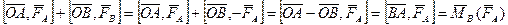
Не зависит от выбора точки 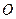
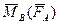 перпендикулярен плоскости пары.
перпендикулярен плоскости пары.
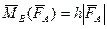
 Момент пары сил полностью характеризует пару.
Момент пары сил полностью характеризует пару.
Как расположены плоскости для эквивалентной пары сил?- Они параллельны.
Чему равен главный вектор пары сил? = 0.
БИЛЕТ 20.
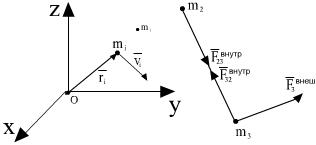 Все точки системы находятся под действием силы.
Все точки системы находятся под действием силы.
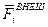 - силы, действующие на точки системы со стороны внешних по отношению к этой системе тел.
- силы, действующие на точки системы со стороны внешних по отношению к этой системе тел.
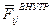 - силы, действующие между точками системы.
- силы, действующие между точками системы.
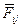 - сила, действующая на
- сила, действующая на 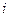 -ю точку со стороны
-ю точку со стороны 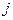 - й точки системы.
- й точки системы.
По третьему закону Ньютона: 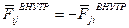 . Они равны по модулю и действуют по прямой, их соединяющей, в противоположные стороны.
. Они равны по модулю и действуют по прямой, их соединяющей, в противоположные стороны.
Тогда для 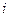 -й точки системы:
-й точки системы:
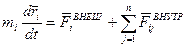
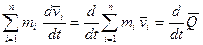 - слева.
- слева.
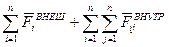 =
= 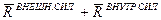 .
.
Главный вектор внутренних сил 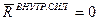 , потому что все силы встречаются парами равными по величине и противоположными по направлению.
, потому что все силы встречаются парами равными по величине и противоположными по направлению.
БИЛЕТ 21.
Количеством движения материальной точки называется сумма произведений масс на их скорость.
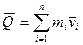 - вектор количества движения.
- вектор количества движения.
 Все эти точки находятся под действием силы.
Все эти точки находятся под действием силы.
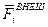 - силы, действующие на точки системы со стороны внешних по отношению к этой системе тел.
- силы, действующие на точки системы со стороны внешних по отношению к этой системе тел.
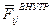 - силы, действующие между точками системы.
- силы, действующие между точками системы.
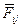 - сила, действующая на
- сила, действующая на 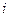 -ю точку со стороны
-ю точку со стороны 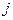 - й точки системы.
- й точки системы.
По третьему закону Ньютона: 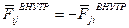 . Они равны по модулю и действуют по прямой, их соединяющей, в противоположные стороны.
. Они равны по модулю и действуют по прямой, их соединяющей, в противоположные стороны.
Тогда для 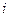 -й точки системы:
-й точки системы:
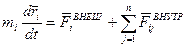
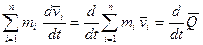 - слева.
- слева.
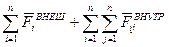 =
= 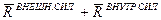 .
.
Главный вектор внутренних сил 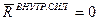 , потому что все силы встречаются парами равными по величине и противоположными по направлению.
, потому что все силы встречаются парами равными по величине и противоположными по направлению.
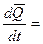
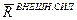 - теорема об изменении количества движения системы материальных точек в инерциальной системе отсчета.
- теорема об изменении количества движения системы материальных точек в инерциальной системе отсчета.
Производная по времени от вектора количества движения равна главному вектору внешних сил.
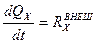 ,
, 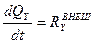 ,
, 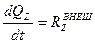 .
.
Система материальных точек называется замкнутой, если на нее не действуют внешние силы; и если на систему не действуют внешние силы, то вектор количества движения (импульса) есть величина постоянная.
БИЛЕТ 22.
Центр масс системы материальных точек- это точка, полжение которой в пространстве опредляется вектором 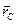 .
.
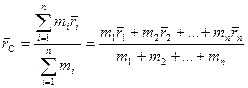 .
.
 Координаты центра масс:
Координаты центра масс:
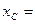
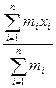
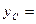
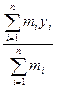
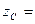
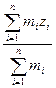
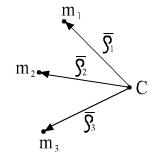
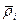 - радиус-вектор относительно центра масс.
- радиус-вектор относительно центра масс.
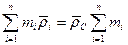 , но
, но 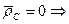
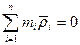
Связь вектора количества движения со скоростью центра масс:
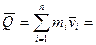
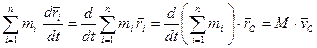
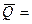
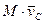 , где
, где 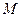 - масса всей системы.
- масса всей системы. 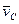 - скорость центра масс.
- скорость центра масс.
Тогда из теоремы изменения количества движения следует теорема о движении центра масс:
Центр масс системы движется как материальная точка, в которой сосредоточена вся масса системы и на которую действует сила, равная главному вектору внешних сил.
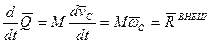
Если 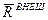 = 0, то центр масс системы находится в покое или в состоянии равномерного прямолинейного движения.
= 0, то центр масс системы находится в покое или в состоянии равномерного прямолинейного движения.
БИЛЕТ 23.
Кинетическим моментом системы материальных точек относительно точки 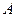 называется сумма векторных произведений радиус-векторов относительно точки
называется сумма векторных произведений радиус-векторов относительно точки 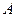 на импульс точек.
на импульс точек.
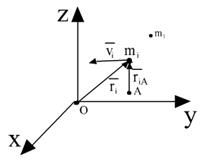
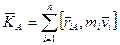
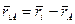
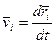
Инерциональная с.о.
Пример:
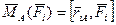
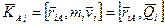
Дата добавления: 2016-04-23; просмотров: 9942;
