Простейшие матричные уравнения
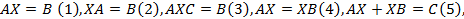
где 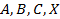 – матрицы таких размеров, что все используемые операции возможны, а левые и правые части этих матричных уравнений представляют собой матрицы одинаковых размеров.
– матрицы таких размеров, что все используемые операции возможны, а левые и правые части этих матричных уравнений представляют собой матрицы одинаковых размеров.
Решение уравнений (1)-(3) возможно с помощью обратных матриц в случае невырожденности матриц при Х. В общем случае матрицу Х записывают поэлементно и проводят указанные в уравнении действия над матрицами. В результате получают систему линейных уравнений. Решив систему, находят элементы матрицы Х.
Метод обратной матрицы
Это решение системы линейных уравнений в случае квадратной невырожденной матрицы системы А. Находится из матричного уравнения АХ=В.
А-1(АХ)=А-1В, (А-1А)Х=А-1В, ЕХ= А-1В, Х= А-1В.
Формулы Крамера
Теорема.Пусть Δ - определитель матрицы системы А, а Δj - определитель матрицы, получаемый из матрицы А заменой j-го столбцом свободных членов. Тогда, если Δ≠0, то система имеет единственное решение, определяемое по формулам:
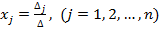 - формулы Крамера.
- формулы Крамера.
ДЗ 1. 2.23, 2.27, 2.51,2.55, 2.62; ДЗ 2.2.19, 2.26, 2.40,2.65
Тема 4. Комплексные числа и многочлены
Комплексные числа и действия над ними
Определения.
1. Символ вида a + bi , где a и b произвольные действительные числа, условимся называть комплексным числом.
2. Комплексные числа a + bi и a1 + b1i условимся считать равными, если а = а1 и
b = b1.
3. Комплексное число вида a + 0i условимся считать равным действительному числу а.
4. Суммой двух комплексных чисел a + bi и a1 + b1i называется комплексное число (а + а1) + (b + b1)i.
5. Произведением двух комплексных чисел называется комплексное число aa1 – bb1 + (a b1 +a1b)i.
Комплексное число вида 0 + bi называется чисто мнимым числом и обычно записывается так: bi; число 0 +1i = i называется мнимой единицей.
В силу определения 3 всякому действительному числу а соответствует «равное» комплексное число a + 0i и обратно – всякому комплексному числу a + 0i соответствует «равное» действительное число а, то есть между этими числами существует взаимно-однозначное соответствие. Если рассмотреть сумму и произведение комплексных чисел a1 + 0i и a2 + 0i по правилам 4 и 5, то получим:
(a1 + 0i) + (a2 + 0i) = (a1 + a2) + 0i,
(a1 + 0i) (a2 + 0i) = (a1 a2 – 0) + (a10+a20) i = a1a2 + 0i.
Мы видим, что сумме (или произведению) данных комплексных чисел соответствует действительное число, «равное» сумме (или произведению) соответствующих действительных чисел. Итак, соответствие между комплексными числами вида a + 0i и действительным числом а таково, что в результате выполнения арифметических действий над соответствующими компонентами получаются соответственные результаты. Взаимно-однозначное соответствие, которое сохраняется при выполнении действий, называется изоморфизмом. Это позволяет отождествить число a + 0i с действительным числом а и рассматривать всякое действительное число как частный случай комплексного.
Следствие. Квадрат числа i равен – 1.
i 2 = i i = (0 +1i)( 0 +1i) = (0 – 1) + (0·1 + 1·0)i = - 1.
Теорема. Для сложения и умножения комплексных чисел остаются в силе основные законы действий.
Определения:
1. Действительное число а называется действительной частью комплексного числа z = a + bi. Rez=a
2. Число b называется мнимой частью комплексного числа z, число b - коэффициентом при мнимой части z. Imz=b.
3. Числа a + bi и a – bi называются сопряжёнными.
Число, сопряжённое числу z = a + bi обозначается символом
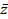 = a - bi.
= a - bi.
Пример. z =3 + i , 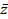 = 3 - i.
= 3 - i.
Теорема. Сумма и произведение двух сопряжённых комплексных чисел действительны.
Доказательство. Имеем
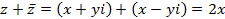
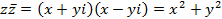 .
.
В множестве комплексных чисел выполнимы действия, обратные сложению и умножению.
Вычитание. Пусть z1 = a1 + b1i и z2 = a2 + b2i - данные комплексные числа. разность z1 – z2 есть число z = x + y i, удовлетворяющее условию z1 = z2 + z или
а1 + b1i = (a2 + x) + (b2 + y)i.
Для определения x и y получаем систему уравнений a2 + x = а1 и b2 + y = b1, имеющую единственное решение:
x = а1 - a2, y = b1 - b2,
откуда
z = (а1 + b1i) – (а2 + b2i) = а1 – а2 +( b1 - b2)i.
Вычитание можно заменить сложением с числом, противоположным вычитаемому:
z = (а1 + b1i) – (а2 + b2i) = (а1 + b1i) + (- а2 - b2i).
Деление. Частное чисел z1 и z2≠ 0 есть число z = x + y i , удовлетворяющее условию z1 = z2z или
а1 + b1i = (a2 + b2i) (x + yi),
следовательно,
а1 + b1i = a2 x - b2y+ (b2x + a2y)i,
откуда получаем систему уравнений:
a2 x - b2y = a1,
b2x + a2y = b1.
Решением которой будут
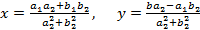 ,
,
следовательно,
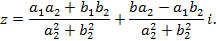
Практически для нахождения частного  умножают делимое и делитель на число
умножают делимое и делитель на число 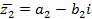 , сопряжённое делителю:
, сопряжённое делителю:
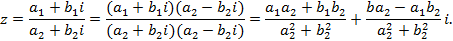
Так, например,
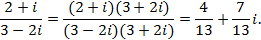
В частности число  , обратное данному числу z , можно представить в виде
, обратное данному числу z , можно представить в виде
 .
.
Примечание. В множестве комплексных чисел остаётся в силе теорема: еслипроизведение равно нулю, то хотя бы один из сомножителей равен нулю.
В самом деле, если z1z2 =0 и если z1≠ 0, то умножая на  , получим
, получим

что и требовалось доказать.
При выполнении арифметических действий над комплексными числами надлежит руководствоваться следующим общим правилом: действия выполняются по обычным правилам действий над алгебраическими выражениями с последующей заменой i2 на -1.
Теорема. При замене каждого из компонентов сопряжённым ему числом результат действия тоже заменяется сопряжённым числом.
Доказательство заключается в непосредственной проверке. Так, например, если каждое слагаемое z1 = a1 + b1i и z2 = a2 + b2i заменить сопряжённым числом, то получим число, сопряжённое сумме z1 + z2.
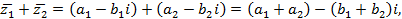
cледовательно,
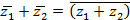 .
.
Аналогично для произведения имеем:
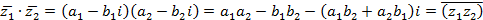 .
.
Дата добавления: 2016-10-17; просмотров: 844;
