Критерий Сильвестра знакоопределенности квадратичной формы
Знакоопределенность квадратичной формы можно установить, исследуя главные миноры матрицы 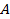 . Такой способ называется критерием Сильвестра:
. Такой способ называется критерием Сильвестра:
Действительная квадратичная форма является положительно определенной тогда и только тогда, когда все главные миноры ее матрицы положительны:
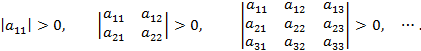
Действительная квадратичная форма является отрицательно определенной тогда и только тогда, когда знаки главных миноров ее матрицы чередуются, причем 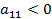 :
:
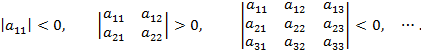
Пример 4.2.1. Методом Лагранжа найти нормальный вид и невырожденное преобразование, приводящее к этому виду, для следующей квадратичной формы.
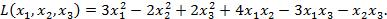
Решение: Метод Лагранжа заключается в выделении полных квадратов по всем переменным:
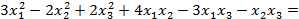
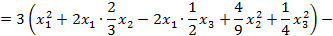
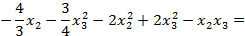
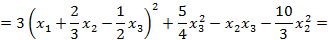
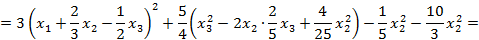
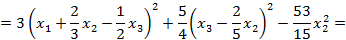
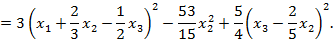
Пусть
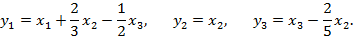
Тогда исходная квадратичная форма может быть приведена к каноническому виду
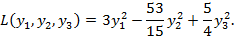
Сделав замену
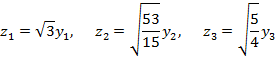
получим нормальный вид квадратичной формы
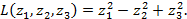
Ответ: Квадратичная форма
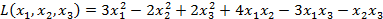
может быть приведена к нормальному виду
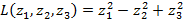
с помощью невырожденного преобразования
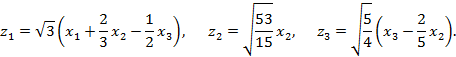
Тема 6. Элементы аналитической геометрии
Прямая и плоскость
Прямой в пространстве 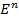 , проходящей через точку
, проходящей через точку 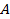 с координатами
с координатами 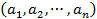 , параллельно вектору
, параллельно вектору 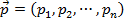 , называется множество точек
, называется множество точек 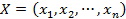 вида
вида
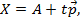
где 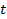 – любое число. Вектор
– любое число. Вектор 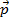 называется направляющим вектором прямой.
называется направляющим вектором прямой.
В координатах равенство 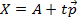 можно записать
можно записать
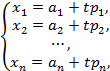
или чисто символически
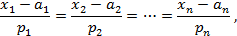
поскольку некоторые из координат вектора 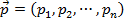 могут равняться нулю.
могут равняться нулю.
Определение.Пусть А и В две точки пространства. Отрезком АВ назовём множество точек Х вида
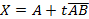 ,
,
uде t принимает любое значение из промежутка [0, 1].
k-мерной плоскостью в пространстве 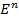 , проходящей через точку
, проходящей через точку 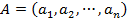 , параллельно линейно независимой системе k векторов
, параллельно линейно независимой системе k векторов 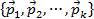 , называется множество точек
, называется множество точек
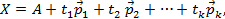
где 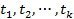 – произвольные числа.
– произвольные числа.
Одномерная плоскость – это прямая; n-мерная плоскость в пространстве 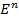 совпадает с этим пространством.
совпадает с этим пространством.
Гиперплоскость – это (n-1)-мерная плоскость в пространстве 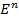 , которая задается одним линейным уравнением
, которая задается одним линейным уравнением
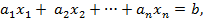
где 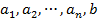 – константы, причем не все числа
– константы, причем не все числа 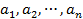 равны нулю.
равны нулю.
Вектором нормали гиперплоскости
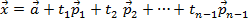
называется вектор 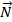 , такой, что
, такой, что 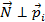 для всех
для всех 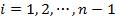 . То есть
. То есть
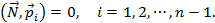
Тогда для точек гиперплоскости в 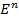 имеем уравнение
имеем уравнение
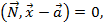
которое называется векторным общим уравнением гиперплоскости в 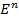 .
.
Пусть 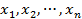 – декартова прямоугольная система координат в
– декартова прямоугольная система координат в 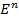 ,
, 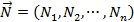 – некоторый вектор, то в координатах уравнение гиперплоскости можно записать в виде:
– некоторый вектор, то в координатах уравнение гиперплоскости можно записать в виде:
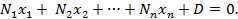
Следовательно, в декартовой системе координат коэффициенты 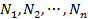 общего уравнения прямой являются координатами вектора нормали гиперплоскости. Здесь
общего уравнения прямой являются координатами вектора нормали гиперплоскости. Здесь 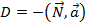 . Если ввести в рассмотрение единичный вектор нормали
. Если ввести в рассмотрение единичный вектор нормали
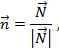
то величина 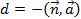 численно равна расстоянию от начала координат до гиперплоскости. Тогда
численно равна расстоянию от начала координат до гиперплоскости. Тогда 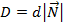 . Положительное (отрицательное) значение
. Положительное (отрицательное) значение 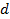 означает, что начало координат находится в нижнем (верхнем) полупространстве относительно данной гиперплоскости. Величина
означает, что начало координат находится в нижнем (верхнем) полупространстве относительно данной гиперплоскости. Величина 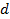 называется отклонением начала координат от гиперплоскости.
называется отклонением начала координат от гиперплоскости.
Пусть 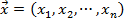 – радиус-вектор произвольной точки
– радиус-вектор произвольной точки 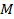 в
в 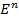 . Отклонением точки
. Отклонением точки 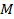 от гиперплоскости является уравнение гиперплоскости:
от гиперплоскости является уравнение гиперплоскости:
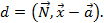
Расстояние от точки 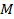 до гиперплоскости определяется как абсолютное значение этой величины
до гиперплоскости определяется как абсолютное значение этой величины 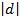 .
.
Зададим гиперплоскость в декартовых координатах
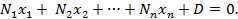
Тогда
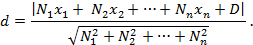
Угол 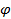 между двумя прямыми:
между двумя прямыми: 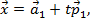
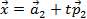 определим из соотношения для скалярного произведения векторов:
определим из соотношения для скалярного произведения векторов:
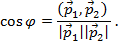
Углом 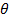 между прямой и гиперплоскостью называется угол между этой прямой и ее ортогональной проекцией на плоскость.
между прямой и гиперплоскостью называется угол между этой прямой и ее ортогональной проекцией на плоскость.
Зададим прямую параметрически 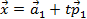 , а плоскость зададим общим уравнением
, а плоскость зададим общим уравнением 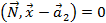 . Тогда
. Тогда
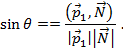
Углом 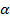 между гиперплоскостями называется угол между прямыми, перпендикулярными заданным плоскостям.
между гиперплоскостями называется угол между прямыми, перпендикулярными заданным плоскостям.
Зададим две гиперплоскости общими уравнениями: 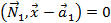 и
и 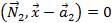 . Тогда
. Тогда
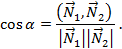
Пусть 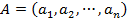 и
и 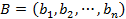 – две произвольные точки. Построим прямую, проходящую через две точки
– две произвольные точки. Построим прямую, проходящую через две точки 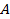 и
и 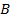 .
.
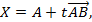
или в координатах
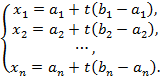
В частности, при 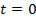 получим точку
получим точку 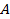 , а при
, а при 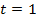 получим точку
получим точку 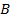 . При
. При 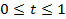 получим замкнутый отрезок, а при
получим замкнутый отрезок, а при 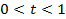 получим открытый отрезок. При
получим открытый отрезок. При 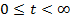 получим луч. Последние равенства можно переписать в виде:
получим луч. Последние равенства можно переписать в виде:
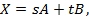
или в координатах
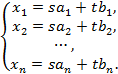
Здесь при описании отрезка числа 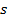 и
и 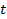 пробегают всевозможные действительные положительные значения, связанные между собой равенством:
пробегают всевозможные действительные положительные значения, связанные между собой равенством: 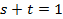 .
.
В декартовых прямоугольных координатах уравнение плоскости в трехмерном пространстве приводиться к виду
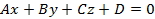
и называется общим уравнением плоскости. Коэффициенты 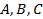 являются координатами вектора
являются координатами вектора 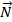 , перпендикулярного к этой плоскости Он называется нормальным вектором этой плоскости и определяет ориентацию плоскости в пространстве относительно системы координат.
, перпендикулярного к этой плоскости Он называется нормальным вектором этой плоскости и определяет ориентацию плоскости в пространстве относительно системы координат.
Существуют различные способы задания плоскости в трехмерном пространстве и соответствующие им виды уравнения.
1. Если плоскость проходит через точку 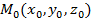 и перпендикулярна к вектору
и перпендикулярна к вектору 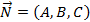 , то ее уравнение записывается в виде:
, то ее уравнение записывается в виде:
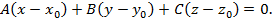
2. Уравнение плоскости в «отрезках». Если плоскость пересекает оси координат 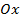 ,
, 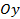 ,
, 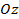 в точках
в точках 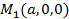 ,
, 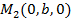 ,
, 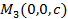 соответственно, то ее уравнение можно записать в виде:
соответственно, то ее уравнение можно записать в виде:
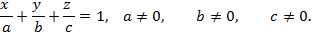
3. Если плоскость проходит через точки 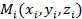 , где
, где 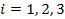 , не лежащие на одной прямой, то ее уравнение можно записать в виде:
, не лежащие на одной прямой, то ее уравнение можно записать в виде:
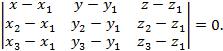
Угол 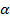 между двумя плоскостями
между двумя плоскостями 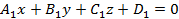 и
и 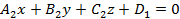 вычисляется на основании формулы:
вычисляется на основании формулы:
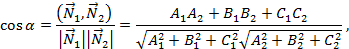
где 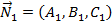 ,
, 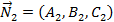 – нормальные векторы данных плоскостей. Отсюда условие перпендикулярности данных плоскостей
– нормальные векторы данных плоскостей. Отсюда условие перпендикулярности данных плоскостей 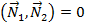 можно представить в виде:
можно представить в виде: 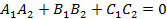 . Условие параллельности рассматриваемых плоскостей:
. Условие параллельности рассматриваемых плоскостей:
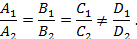
Расстояние 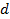 от точки
от точки 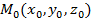 до плоскости, заданной уравнением
до плоскости, заданной уравнением 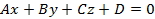 , вычисляется по формуле:
, вычисляется по формуле:
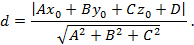
Пример. При каких значениях параметра α плоскость, заданная уравнением 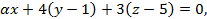 перпендикулярна координатной плоскости
перпендикулярна координатной плоскости 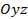 ?
?
Решение: Воспользуемся условием перпендикулярности
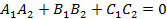
двух плоскостей, заданных уравнениями
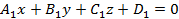 ,
,
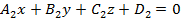 .
.
По условию задачи первая плоскость, заданная уравнением
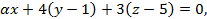
или
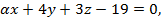
имеет следующие значения коэффициентов
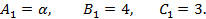
Координатная плоскость 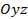 , заданная уравнением
, заданная уравнением 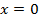 , имеет значения коэффициентов
, имеет значения коэффициентов
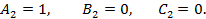
Таким образом, условие перпендикулярности
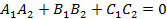
этих плоскостей можно представить в виде:
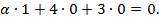
Отсюда следует, что 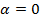 .
.
Ответ: Плоскость, заданная уравнением 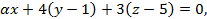 перпендикулярна координатной плоскости
перпендикулярна координатной плоскости 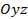 при
при 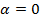 .
.
Пример. Составить уравнение плоскости, проходящей через точку 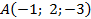 , параллельно двум неколлинеарным векторам
, параллельно двум неколлинеарным векторам 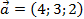 и
и 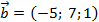 .
.
Решение: Составим уравнение плоскости по точке и двум неколлинеарным векторам:
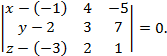
Вычислим определитель, разложив его по первому столбцу
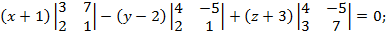
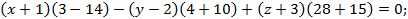
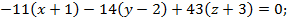
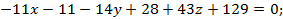
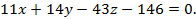
Ответ: Уравнение плоскости, проходящей через точку 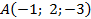 , параллельно двум неколлинеарным векторам
, параллельно двум неколлинеарным векторам 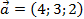 и
и 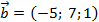 , можно представить в виде:
, можно представить в виде: 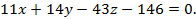
Пример. Составить уравнение плоскости, проходящей через точку 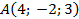 перпендикулярно вектору
перпендикулярно вектору 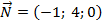 .
.
Решение: Воспользуемся формулой
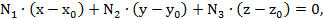
где 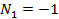 ,
, 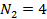 ,
, 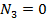 – координаты вектора
– координаты вектора 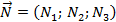 ;
; 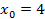 ,
, 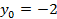 ,
, 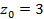 – координаты точки
– координаты точки 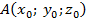 . Получим
. Получим
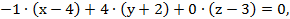
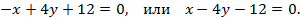
Ответ: Уравнение плоскости, проходящей через точку 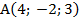 перпендикулярно вектору
перпендикулярно вектору 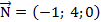 можно представить в виде:
можно представить в виде:
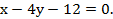
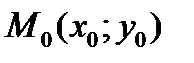 Прямая на плоскости
Прямая на плоскости
1. Уравнение прямой, проходящей через заданную точку перпендикулярно заданному вектору 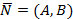
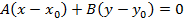
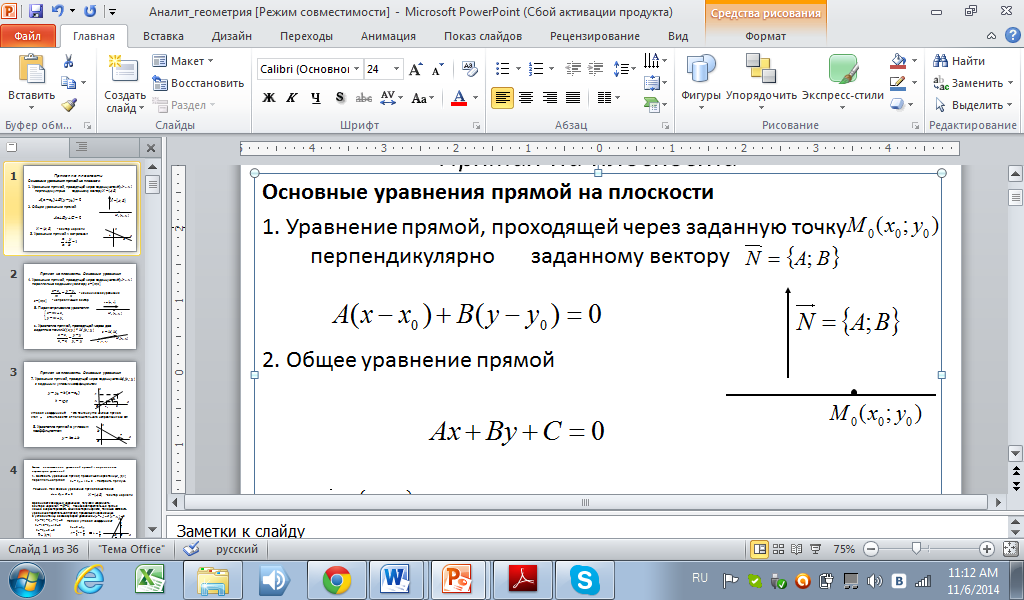
2. Общее уравнение прямой
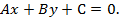
3. Уравнение прямой в отрезках
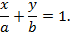
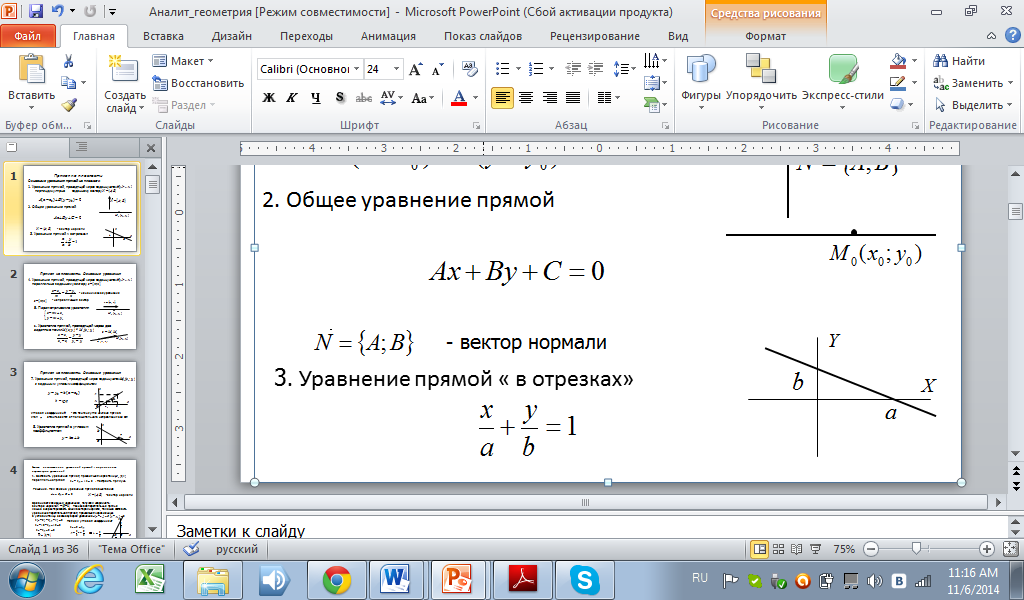
4. Уравнение прямой, проходящей через заданную точку 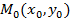 параллельно заданному вектору
параллельно заданному вектору 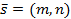 (направляющий вектор прямой).
(направляющий вектор прямой).
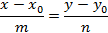
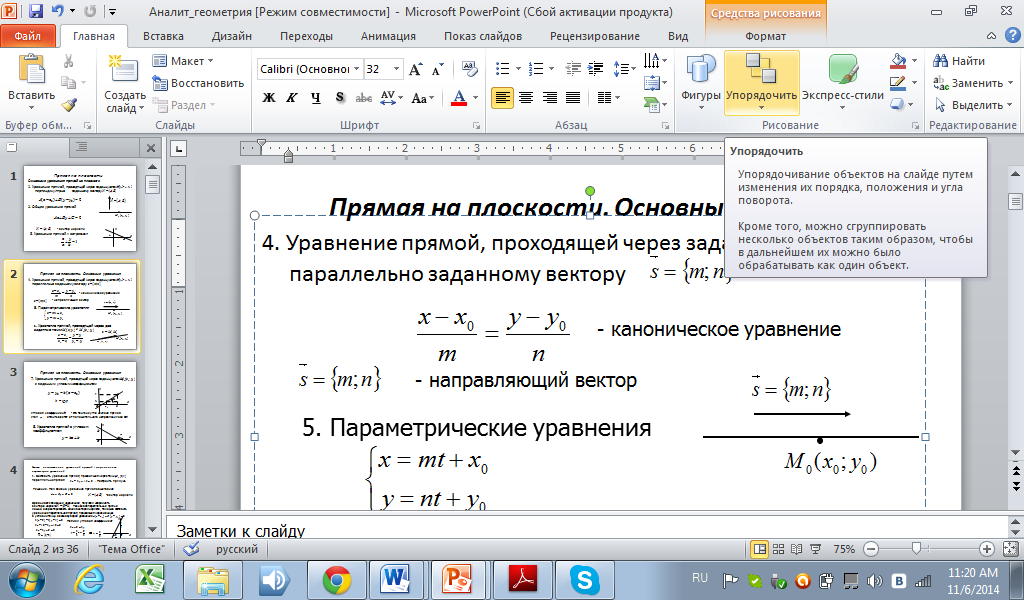
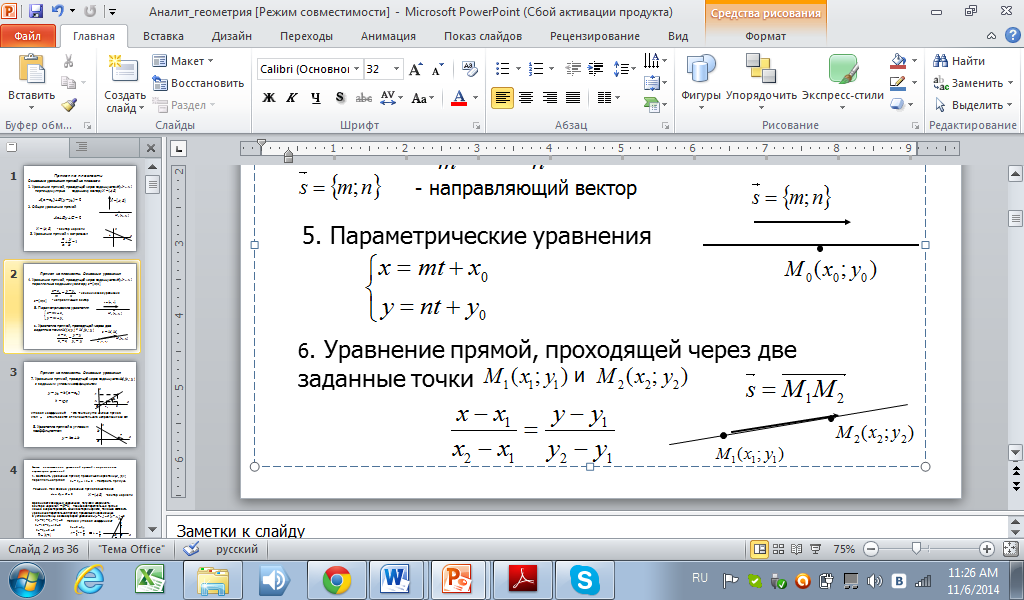
5. Параметрические уравнения
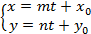 .
.
6. Уравнение прямой, проходящей через две точки 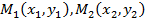
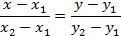
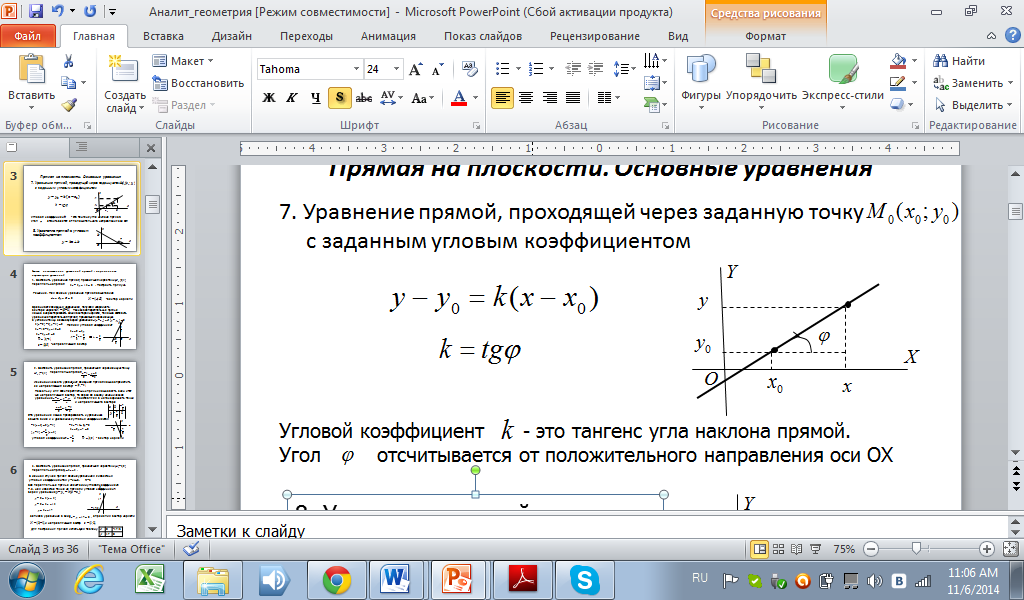
7. Уравнение прямой, проходящей через заданную точку 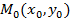 с заданным угловым коэффициентом
с заданным угловым коэффициентом
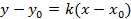
Угловой коэффициент k - это тангенс угла наклона прямой.
Угол 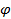 отсчитывается от положительного направления оси OX
отсчитывается от положительного направления оси OX
8. Уравнение прямой с угловым коэффициентом
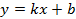
Дата добавления: 2016-10-17; просмотров: 3137;
