Кривые второго порядка.

Кривая второго порядка – геометрическое место точек плоскости, прямоугольные координаты которых удовлетворяют уравнению вида

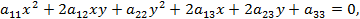
в котором, по крайней мере, один из коэффициентов 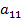, , 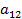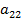отличен от нуля. Общее уравнение кривой можно записать в матричном виде

Невырожденная кривая второго порядка при

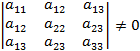
оказывается вещественным эллипсом, мнимым эллипсом, гиперболой или параболой в зависимости от того, будет ли квадратичная форма

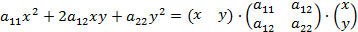
положительно определённой, отрицательно определённой, неопределённой или полуопределённой, что устанавливается по корням характеристического уравнения:

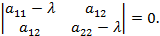
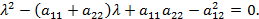
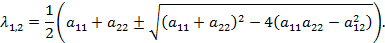
Вводом новой системы координат 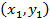можно привести уравнения кривых второго порядка к стандартному каноническому виду. Для каждой кривой 2-го порядка (для каждого уравнения) существует такая система координат, в которой уравнение кривой имеет вид окружности, эллипса, гиперболы или параболы.

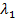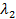1. Если собственные значения и одного знака, то уравнение кривой второго порядка можно привести к уравнению эллиптического типа:

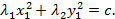
Есл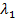и и 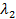имеют тот же знак, что и 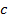, то имеем каноническое уравнение эллипса:

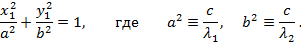
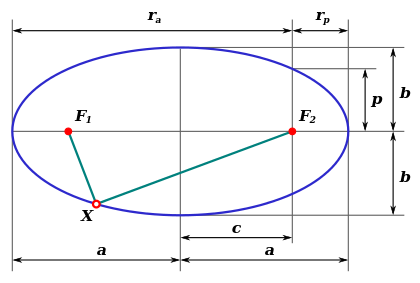
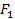Эллипс – геометрическое место точек плоскости, для которых сумма расстояний до двух данных точек и 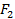, называемых фокусами, постоянна и больше расстояния между фокусам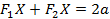и: при .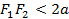

Если 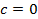, то уравнение 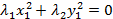имеет единственное решение при 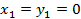, определяющее точку на плоскости.

Есл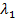и и 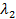имеют знак, противоположный знаку 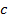, то имеем пустое множество решений, иногда называемое мнимым эллипсом:

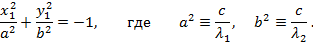
2. Если собственные значения 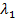и 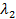разных знаков, то уравнение кривой второго порядка можно привести к уравнению гиперболического типа:

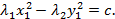
При 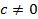оно сводится к одному из двух уравнений

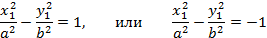
в зависимости от знака 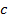. Оба этих уравнения определяют гиперболу – геометрическое место точек 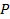плоскости, для которых абсолютное значение разности расстояний от точки 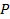до двух выделенных точек 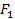и 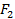, называемых фокусами, постоянно: 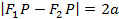при .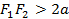

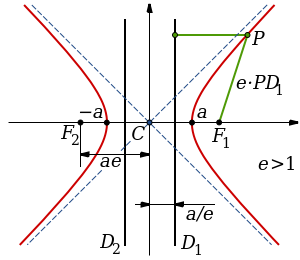
При 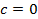получаем уравнение

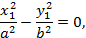
эквивалентное двум линейным уравнениям:

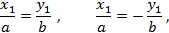
задающим пару пересекающих прямых.

3. Если одно из собственных значени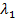й или 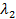равно нулю, то уравнение кривой второго порядка можно привести к уравнению параболического типа, которое можно привести к одному из следующих видов:

Уравнение 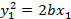определяет параболу– геометрическое место точек 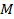, равноудаленных от данной прямой 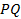, называемой директрисой, и данной точки 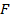, называемой фокусом параболы: .

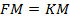Уравнение 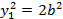, или 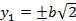определяет парупараллельных прямых.

Уравнение 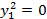определяет пару совпадающих прямых.

Уравнение 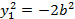не имеет решений, следовательно, не определяет никакого геометрического образа.

Пример. Записать в каноническом виде уравнение эллипса, проходящего через точки:

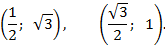
Решение: Каноническое уравнение эллипса, координатные оси которого совпадают с осями эллипса, имеет вид:

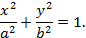
Значения осей эллипса 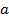и 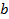найдем из двух условий:

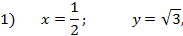
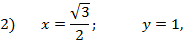
известных по условию задачи. Подставим эти значения в каноническое уравнение эллипса. Получим систему двух уравнений:

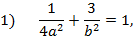
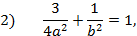
Разрешив систему этих двух уравнений относительно неизвестных 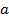и 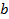, например, методом исключения, получим 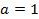, 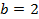. Таким образом, каноническое уравнение эллипса имеет вид:

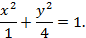
Ответ: Каноническое уравнение эллипса, проходящего через точки:

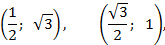
имеет вид:

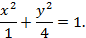
Пример. Уравнение гиперболы

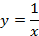
привести к каноническому виду.

Решение: В уравнении гиперболы 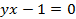сделаем замену переменных:

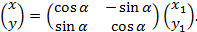
Тогда

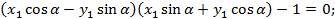
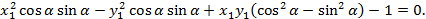
Поскольку каноническое уравнение гиперболы

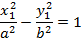
не содержит произведение 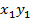, из условия 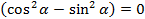следует, что 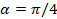. Подставляя значение 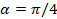в уравнение

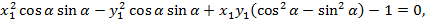
получим

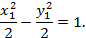
Ответ: Уравнение гиперболы

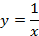
имеет канонический вид:

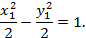
Пример. Определить вид кривой, определяемой уравнением

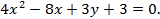
Вычислить основные параметры этой кривой.

Решение. Преобразуем исходное уравнение.

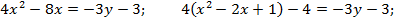
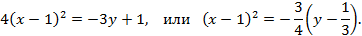
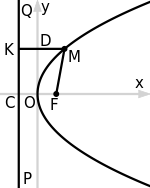
Последнее уравнение является каноническим уравнением параболы 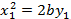с вершиной в точке

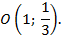
Ветви параболы направлены вниз.

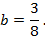
Фокус имеет координаты:

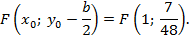
Директриса:

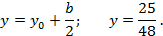
Ответ: Кривая, определяемая уравнением 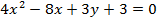, является параболой

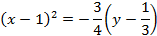
с ветвями, направленными вниз, с директрисой 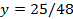, с фокусом в точке с координатами 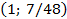, с вершиной в точке с координатами .

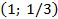6.3. Выпуклые множества в пространстве Rⁿ

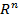Определение.Множество пространства называется выпуклым, если вместе с любыми двумя точкам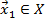и и 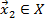ему принадлежит и соединяющий их отрезок .

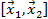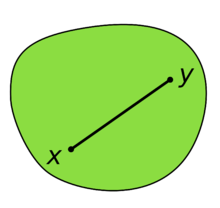
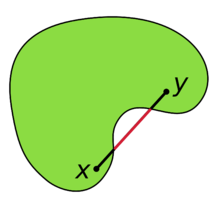
Выпуклое множество. Невыпуклое множество.

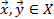Выпуклость множества означает, что из следует 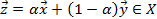для всех 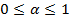. Например, на плоскости в двумерном пространстве 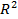– это отрезок, полупрямая, круг, треугольник, полуплоскость и вся плоскость.

Определение. Полупространством в п-мерном пространстве 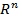называется множество всех точек 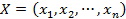, координаты которых удовлетворяют заданному неравенству первой степени:

,

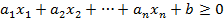Где 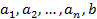– фиксированные числа, причём 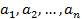не все равны нулю.

Теорема.Любое полупространство есть выпуклое множеством.

Доказательство. Рассмотрим две точк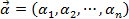и и 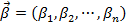в пространстве 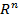, принадлежащих, например, полупространству 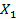. Тогда

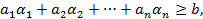
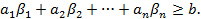
Если 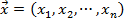– произвольная точка отрезка 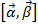, то

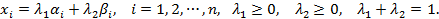
Для этой точки 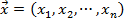имеем:

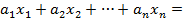
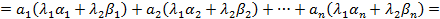
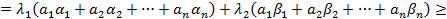
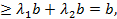
т.е. произвольная точка 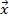отрезка 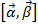принадлежит 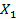, что и требовалось показать.

Лемма. Пересечение любого числа выпуклых множеств есть множество выпуклое. Доказательство. Рассмотрим 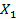, , 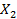, 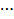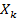– выпуклые множества в пространстве 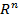. Если пересечение 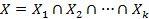состоит из одной точки, то оно выпукло. Если пересечение состоит из более чем одной точки, то пусть 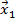и 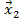– любые две из них. Тогда 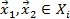для всех 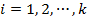и, так как все множества 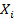выпуклы, то 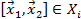и, следовательно, 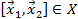, что и требовалось показать.

Отсюда следует, что гиперплоскость как пересечение выпуклых множеств 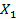и 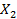является выпуклым множеством. Каждая k-мерная плоскость в пространстве 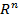также выпукла.

Определение.Пусть в пространстве 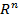даны 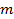полупространств, определяемых неравенствами

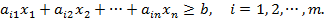
Пересечение этих полупространств, называемое выпуклой многогранной областью, определяет множество решений данной системы линейных неравенств. Если это пересечение ограничено, оно называется выпуклым многогранником в пространстве .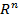

Определение.Точка С выпуклой многогранной области М называется вершиной,или угловой точкой, области М, если не существует представления С в виде

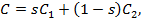
где 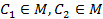и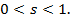

Теорема.Выпуклый п – мерный многогранник является выпуклой линейной комбинацией своих угловых точек